Stanford Encyclopedia of Philosophy
This is a file in the archives of the Stanford Encyclopedia of Philosophy.

Connectionism

First published Sun May 18, 1997; substantive revision Wed Mar 7, 2007

Connectionism is a movement in cognitive science which hopes to explain human intellectual abilities using artificial neural networks (also known as ‘neural networks’ or ‘neural nets’). Neural networks are simplified models of the brain composed of large numbers of units (the analogs of neurons) together with weights that measure the strength of connections between the units. These weights model the effects of the synapses that link one neuron to another. Experiments on models of this kind have demonstrated an ability to learn such skills as face recognition, reading, and the detection of simple grammatical structure.

Philosophers have become interested in connectionism because it promises to provide an alternative to the classical theory of the mind: the widely held view that the mind is something akin to a digital computer processing a symbolic language. Exactly how and to what extent the connectionist paradigm constitutes a challenge to classicism has been a matter of hot debate in recent years.

1. A Description of Neural Networks

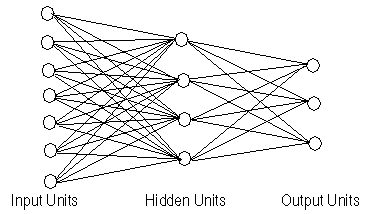
A neural network consists of large number of units joined together in a pattern of connections. Units in a net are usually segregated into three classes: input units, which receive information to be processed, output units where the results of the processing are found, and units in between called hidden units. If a neural net were to model the whole human nervous system, the input units would be analogous to the sensory neurons, the output units to the motor neurons, and the hidden units to all other neurons.

Here is a simple illustration of a simple neural net:

net

Each input unit has an activation value that represents some feature external to the net. An input unit sends its activation value to each of the hidden units to which it is connected. Each of these hidden units calculates its own activation value depending on the activation values it receives from the input units. This signal is then passed on to output units or to another layer of hidden units. Those hidden units compute their activation values in the same way, and send them along to their neighbors. Eventually the signal at the input units propagates all the way through the net to determine the activation values at all the output units.

The pattern of activation set up by a net is determined by the weights, or strength of connections between the units. Weights may be both positive or negative. A negative weight represents the inhibition of the receiving unit by the activity of a sending unit. The activation value for each receiving unit is calculated according a simple activation function. Activation functions vary in detail, but they all conform to the same basic plan. The function sums together the contributions of all sending units, where the contribution of a unit is defined as the weight of the connection between the sending and receiving units times the sending unit's activation value. This sum is usually modified further, for example, by adjusting the activation sum to a value between 0 and 1 and/or by setting the activation to zero unless a threshold level for the sum is reached. Connectionists presume that cognitive functioning can be explained by collections of units that operate in this way. Since it is assumed that all the units calculate pretty much the same simple activation function, human intellectual accomplishments must depend primarily on the settings of the weights between the units.

The kind of net illustrated above is called a feed forward net. Activation flows directly from inputs to hidden units and then on to the output units. More realistic models of the brain would include many layers of hidden units, and recurrent connections that send signals back from higher to lower levels. Such recurrence is necessary in order to explain such cognitive features as short term memory. In a feed forward net, repeated presentations of the same input produce the same output every time, but even the simplest organisms habituate to (or learn to ignore) repeated presentation of the same stimulus. Connectionists tend to avoid recurrent connections because little is understood about the general problem of training recurrent nets. However Elman (1991) and others have made some progress with simple recurrent nets, where the recurrence is tightly constrained.

2. Neural Network Learning and Backpropagation

Finding the right set of weights to accomplish a given task is the central goal in connectionist research. Luckily, learning algorithms have been devised that can calculate the right weights for carrying out many tasks. (See Hinton 1992 for an accessible review.) One of the most widely used of these training methods is called backpropagation. To use this method one needs a training set consisting of many examples of inputs and their desired outputs for a given task. If, for example, the task is to distinguish male from female faces, the training set might contain pictures of faces together with an indication of the sex of the person depicted in each one. A net that can learn this task might have two output units (indicating the categories male and female) and many input units, one devoted to the brightness of each pixel (tiny area) in the picture. The weights of the net to be trained are initially set to random values, and then members of the training set are repeatedly exposed to the net. The values for the input of a member are placed on the input units and the output of the net is compared with the desired output for this member. Then all the weights in the net are adjusted slightly in the direction that would bring the net's output values closer to the values for the desired output. For example, when male's face is presented to the input units the weights are adjusted so that the value of the male output unit is increased and the value of the female output unit is decreased. After many repetitions of this process the net may learn to produce the desired output for each input in the training set. If the training goes well, the net many also have learned to generalize to the desired behavior for inputs and outputs that were not in the training set. For example, it may do a good job of distinguishing males from females in pictures that were never presented to it before.

Training nets to model aspects of human intelligence is a fine art. Success with backpropagation and other connectionist learning methods may depend on quite subtle adjustment of the algorithm and the training set. Training typically involves hundreds of thousands of rounds of weight adjustment. Given the limitations of computers presently available to connectionist researchers, training a net to perform an interesting task may take days or even weeks. Some of the difficulty may be resolved when parallel circuits specifically designed to run neural network models are widely available. But even here, some limitations to connectionist theories of learning will remain to be faced. Humans (and many less intelligent animals) display an ability to learn from single events; for example an animal that eats a food that later causes gastric distress will never try that food again. Connectionist learning techniques such as backpropagation are far from explaining this kind of ‘one shot’ learning.

3. Samples of What Neural Networks Can Do

Connectionists have made significant progress in demonstrating the power of neural networks to master cognitive tasks. Here are three well-known experiments that have encouraged connectionists to believe that neural networks are good models of human intelligence. One of the most attractive of these efforts is Sejnowski and Rosenberg's 1987 work on a net that can read English text called NETtalk. The training set for NETtalk was a large data base consisting of English text coupled with its corresponding phonetic output, written in a code suitable for use with a speech synthesizer. Tapes of NETtalk's performance at different stages of its training are very interesting listening. At first the output is random noise. Later, the net sounds like it is babbling, and later still as though it is speaking English double-talk (speech that is formed of sounds that resemble English words). At the end of training, NETtalk does a fairly good job of pronouncing the text given to it. Furthermore, this ability generalizes fairly well to text that was not presented in the training set.

Another influential early connectionist model was a net trained by Rumelhart and McClelland (1986) to predict the past tense of English verbs. The task is interesting because although most of the verbs in English (the regular verbs) form the past tense by adding the suffix ‘-ed’, many of the most frequently verbs are irregular (‘is’ / ‘was’, ‘come’ / ‘came’, ‘go’ / ‘went’). The net was first trained on a set containing a large number of irregular verbs, and later on a set of 460 verbs containing mostly regulars. The net learned the past tenses of the 460 verbs in about 200 rounds of training, and it generalized fairly well to verbs not in the training set. It even showed a good appreciation of "regularities" to be found among the irregular verbs (‘send’ / ‘sent’, ‘build’ / ‘built’; ‘blow’ / ‘blew’, ‘fly’ / ‘flew’). During learning, as the system was exposed to the training set containing more regular verbs, it had a tendency to overregularize, i.e., to combine both irregular and regular forms: (‘break’ / ‘broked’, instead of ‘break’ / ‘broke’). This was corrected with more training. It is interesting to note that children are known to exhibit the same tendency to overregularize during language learning. However, there is hot debate over whether Rumelhart and McClelland's is a good model of how humans actually learn and process verb endings. For example, Pinker & Prince (1988) point out that the model does a poor job of generalizing to some novel regular verbs. They believe that this is a sign of a basic failing in connectionist models. Nets may be good at making associations and matching patterns, but they have fundamental limitations in mastering general rules such as the formation of the regular past tense. These complaints raise an important issue for connectionist modelers, namely whether nets can generalize properly to master cognitive tasks involving rules. Despite Pinker and Prince's objections, many connectionists believe that generalization of the right kind is still possible (Niklasson and van Gelder 1994).

Elman's 1991 work on nets that can appreciate grammatical structure has important implications for the debate about whether neural networks can learn to master rules. Elman trained a simple recurrent network to predict the next word in a large corpus of English sentences. The sentences were formed from a simple vocabulary of 23 words using a subset of English grammar. The grammar, though simple, posed a hard test for linguistic awareness. It allowed unlimited formation of relative clauses while demanding agreement between the head noun and the verb. So for example, in the sentence

Any man that chases dogs that chase cats … runs.

the singular ‘man’ must agree with the verb ‘runs’ despite the intervening plural nouns (‘dogs’, ‘cats’) which might cause the selection of ‘run’. One of the important features of Elman's model is the use of recurrent connections. The values at the hidden units are saved in a set of so called context units, to be sent back to the input level for the next round of processing. This looping back from hidden to input layers provides the net with a rudimentary form of memory of the sequence of words in the input sentence. Elman's nets displayed an appreciation of the grammatical structure of sentences that were not in the training set. The net's command of syntax was measured in the following way. Predicting the next word in an English sentence is, of course, an impossible task. However, these nets succeeded, at least by the following measure. At a given point in an input sentence, the output units for words that are grammatical continuations of the sentence at that point should be active and output units for all other words should be inactive. After intensive training, Elman was able to produce nets that displayed perfect performance on this measure including sentences not in the training set.

Although this performance is impressive, there is still a long way to go in training nets that can process language. Furthermore, doubts have been raised about the significance of Elman's results. For example, Marcus (1998, 2001) argues that Elman's nets are not able to generalize this performance to sentences formed from a novel vocabulary. This, he claims, is a sign that connectionist models merely associate instances, and are unable to truly master abstract rules. On the other hand, Phillips (2002) argues that classical architectures are no better off in this respect. The purported inability of connectionist models to generalize performance in this way has become an important theme in the systematicity debate. (See Section 7 below.)

4. Strengths and Weaknesses of Neural Network Models

Philosophers are interested in neural networks because they may provide a new framework for understanding the nature of the mind and its relation to the brain (Rumelhart and McClelland 1986, Chapter 1). Connectionist models seem particularly well matched to what we know about neurology. The brain is indeed a neural net, formed from massively many units (neurons) and their connections (synapses). Furthermore, several properties of neural network models suggest that connectionism may offer an especially faithful picture of the nature of cognitive processing. Neural networks exhibit robust flexibility in the face of the challenges posed by the real world. Noisy input or destruction of units causes graceful degradation of function. The net's response is still appropriate, though somewhat less accurate. In contrast, noise and loss of circuitry in classical computers typically result in catastrophic failure. Neural networks are also particularly well adapted for problems that require the resolution of many conflicting constraints in parallel. There is ample evidence from research in artificial intelligence that cognitive tasks such as object recognition, planning, and even coordinated motion present problems of this kind. Although classical systems are capable of multiple constraint satisfaction, connectionists argue that neural network models provide much more natural mechanisms for dealing with such problems.

Over the centuries, philosophers have struggled to understand how our concepts are defined. It is now widely acknowledged that trying to characterize ordinary notions with necessary and sufficient conditions is doomed to failure. Exceptions to almost any proposed definition are always waiting in the wings. For example, one might propose that a tiger is a large black and orange feline. But then what about albino tigers? Philosophers and cognitive psychologists have argued that categories are delimited in more flexible ways, for example via a notion of family resemblance or similarity to a prototype. Connectionist models seem especially well suited to accommodating graded notions of category membership of this kind. Nets can learn to appreciate subtle statistical patterns that would be very hard to express as hard and fast rules. Connectionism promises to explain flexibility and insight found in human intelligence using methods that cannot be easily expressed in the form of exception free principles (Horgan and Tienson 1989, 1990), thus avoiding the brittleness that arises from standard forms of symbolic representation.

Despite these intriguing features, there are some weaknesses in connectionist models that bear mentioning. First, most neural network research abstracts away from many interesting and possibly important features of the brain. For example, connectionists usually do not attempt to explicitly model the variety of different kinds of brain neurons, nor the effects of neurotransmitters and hormones. Furthermore, it is far from clear that the brain contains the kind of reverse connections that would be needed if the brain were to learn by a process like backpropagation, and the immense number of repetitions needed for such training methods seems far from realistic. Attention to these matters will probably be necessary if convincing connectionist models of human cognitive processing are to be constructed. A more serious objection must also be met. It is widely felt, especially among classicists, that neural networks are not particularly good at the kind of rule based processing that is thought to undergird language, reasoning, and higher forms of thought. (For a well known critique of this kind see Pinker and Prince 1988.) We will discuss the matter further when we turn to the systematicity debate.

5. The Shape of the Controversy between Connectionists and Classicists

The last forty years have been dominated by the classical view that (at least higher) human cognition is analogous to symbolic computation in digital computers. On the classical account, information is represented by strings of symbols, just as we represent data in computer memory or on pieces of paper. The connectionist claims, on the other hand, that information is stored non-symbolically in the weights, or connection strengths, between the units of a neural net. The classicist believes that cognition resembles digital processing, where strings are produced in sequence according to the instructions of a (symbolic) program. The connectionist views mental processing as the dynamic and graded evolution of activity in a neural net, each unit's activation depending on the connection strengths and activity of its neighbors, according to the activation function.

On the face of it, these views seem very different. However many connectionists do not view their work as a challenge to classicism and some overtly support the classical picture. So-called implementational connectionists seek an accommodation between the two paradigms. They hold that the brain's net implements a symbolic processor. True, the mind is a neural net; but it is also a symbolic processor at a higher and more abstract level of description. So the role for connectionist research according to the implementationalist is to discover how the machinery needed for symbolic processing can be forged from neural network materials, so that classical processing can be reduced to the neural network account.

However, many connectionists resist the implementational point of view. Such radical connectionists claim that symbolic processing was a bad guess about how the mind works. They complain that classical theory does a poor job of explaining graceful degradation of function, holistic representation of data, spontaneous generalization, appreciation of context, and many other features of human intelligence which are captured in their models. The failure of classical programming to match the flexibility and efficiency of human cognition is by their lights a symptom of the need for a new paradigm in cognitive science. So radical connectionists would eliminate symbolic processing from cognitive science forever.

6. Connectionist Representation

Connectionist models provide a new paradigm for understanding how information might be represented in the brain. A seductive but naive idea is that single neurons (or tiny neural bundles) might be devoted to the representation of each thing the brain needs to record. For example, we may imagine that there is a grandmother neuron that fires when we think about our grandmother. However, such local representation is not likely. There is good evidence that our grandmother thought involves complex patterns of activity distributed across relatively large parts of cortex.

It is interesting to note that distributed, rather than local representations on the hidden units are the natural products of connectionist training methods. The activation patterns that appear on the hidden units while NETtalk processes text serve as an example. Analysis reveals that the net learned to represent such categories as consonants and vowels, not by creating one unit active for consonants and another for vowels, but rather in developing two different characteristic patterns of activity across all the hidden units.

Given the expectations formed from our experience with local representation on the printed page, distributed representation seems both novel and difficult to understand. But the technique exhibits important advantages. For example, distributed representations, (unlike symbols stored in separate fixed memory locations) remain relatively well preserved when parts of the model are destroyed or overloaded. More importantly, since representations are coded in patterns rather than firings of individual units, relationships between representations are coded in the similarities and differences between these patterns. So the internal properties of the representation carry information on what it is about (Clark 1993, 19). In contrast, local representation is conventional. No intrinsic properties of the representation (a unit's firing) determine its relationships to the other symbols. This self-reporting feature of distributed representations promises to resolve a philosophical conundrum about meaning. In a symbolic representational scheme, all representations are composed out of symbolic atoms (like words in a language). Meanings of complex symbol strings may be defined by the way they are built up out of their constituents, but what fixes the meanings of the atoms?

Connectionist representational schemes provide an end run around the puzzle by simply dispensing with atoms. Every distributed representation is a pattern of activity across all the units, so there is no principled way to distinguish between simple and complex representations. To be sure, representations are composed out of the activities of the individual units. But none of these ‘atoms’ codes for any symbol. The representations are sub-symbolic in the sense that analysis into their components leaves the symbolic level behind.

The sub-symbolic nature of distributed representation provides a novel way to conceive of information processing in the brain. If we model the activity of each neuron with a number, then the activity of the whole brain can be given by a giant vector (or list) of numbers, one for each neuron. Both the brain's input from sensory systems and its output to individual muscle neurons can also be treated as vectors of the same kind. So the brain amounts to a vector processor, and the problem of psychology is transformed into questions about which operations on vectors account for the different aspects of human cognition.

Sub-symbolic representation has interesting implications for the classical hypothesis that the brain must contain symbolic representations that are similar to sentences of a language. This idea, often referred to as the language of thought (or LOT) thesis may be challenged by the nature of connectionist representations. It is not easy to say exactly what the LOT thesis amounts to, but van Gelder (1990) offers an influential and widely accepted benchmark for determining when the brain should be said to contain sentence-like representations. It is that when a representation is tokened one thereby tokens the constituents of that representation. For example, if I write ‘John loves Mary’ I have thereby written the sentence's constituents: ‘John’ ‘loves’ and ‘Mary’. Distributed representations for complex expressions like ‘John loves Mary’ can be constructed that do not contain any explicit representation of their parts (Smolensky 1991). The information about the constituents can be extracted from the representations, but neural network models do not need to explicitly extract this information themselves in order to process it correctly (Chalmers 1990). This suggests that neural network models serve as counterexamples to the idea that the language of thought is a prerequisite for human cognition. However, the matter is still a topic of lively debate (Fodor 1997).

The novelty of distributed and superimposed connectionist information storage naturally causes one to wonder about the viability of classical notions of symbolic computation in describing the brain. Ramsey (1997) argues that though we may attribute symbolic representations to neural nets, those attributions do not figure in legitimate explanations of the model's behavior. This claim is important because the classical account of cognitive processing, (and folk intuitions) presume that representations play an explanatory role in understanding the mind. It has been widely thought that cognitive science requires, by its very nature, explanations that appeal to representations (Von Eckardt 2003). If Ramsey is right, the point may cut in two different ways. Some may use it to argue for a new and non-classical understanding of the mind, while others would use it to argue that connectionism is inadequate since it cannot explain what it must. However, Haybron (2000) argues against Ramsey that there is ample room for representations with explanatory role in radical connectionist architectures. Roth (2005) makes the interesting point that contrary to first impressions, it may also make perfect sense to explain a net's behavior by reference to a computer program, even if there is no way to discriminate a sequence of steps of the computation through time.

In a series of papers Horgan and Tienson (1989, 1990) have championed a view called representations without rules. According to this view classicists are right to think that human brains (and good connectionist models of them) contain explanatorily robust representations; but they are wrong to think that those representations enter in to hard and fast rules like the steps of a computer program. The idea that connectionist systems may follow graded or approximate regularities ("soft laws" as Horgan and Tienson call them) is intuitive and appealing. However, Aizawa (1994) argues that given an arbitrary neural net with a representation level description, it is always possible to outfit it with hard and fast representation-level rules. Guarini (2001) responds that if we pay attention to notions of rule following that are useful to cognitive modeling, Aizawa's constructions will seem beside the point.

7. The Systematicity Debate

The major points of controversy in the philosophical literature on connectionism have to do with whether connectionists provide a viable and novel paradigm for understanding the mind. One complaint is that connectionist models are only good at processing associations. But such tasks as language and reasoning cannot be accomplished by associative methods alone and so connectionists are unlikely to match the performance of classical models at explaining these higher-level cognitive abilities. However, it is a simple matter to prove that neural networks can do anything that symbolic processors can do, since nets can be constructed that mimic a computer's circuits. So the objection can not be that connectionist models do not account for higher cognition; it is rather that they can do so only if they implement the classicist's symbolic processing tools. Implementational connectionism may succeed, but radical connectionists will never be able to account for the mind.

Fodor and Pylyshyn's often cited paper (1988) launches a debate of this kind. They identify a feature of human intelligence called systematicity which they feel connectionists cannot explain. The systematicity of language refers to the fact that the ability to produce/understand/think some sentences is intrinsically connected to the ability to produce/understand/think others of related structure. For example, no one with a command of English who understands ‘John loves Mary’ can fail to understand ‘Mary loves John.’ From the classical point of view, the connection between these two abilities can easily be explained by assuming that masters of English represent the constituents (‘John’, ‘loves’ and ‘Mary’) of ‘John loves Mary’ and compute its meaning from the meanings of these constituents. If this is so, then understanding a novel sentence like ‘Mary loves John’ can be accounted for as another instance of the same symbolic process. In a similar way, symbolic processing would account for the systematicity of reasoning, learning and thought. It would explain why there are no people who are capable of concluding P from P & (Q & R), but incapable of concluding P from P & Q, why there are no people capable of learning to prefer a red cube to green square who cannot learn to prefer a green cube to the red square, and why there isn't anyone who can think that John loves Mary who can't also think that Mary loves John.

Fodor and McLaughlin (1990) argue in detail that connectionists do not account for systematicity. Although connectionist models can be trained to be systematic, they can also be trained, for example, to recognize ‘John loves Mary’ without being able to recognize ‘Mary loves John.’ Since connectionism does not guarantee systematicity, it does not explain why systematicity is found so pervasively in human cognition. Systematicity may exist in connectionist architectures, but where it exists, it is no more than a lucky accident. The classical solution is much better, because in classical models, pervasive systematicity comes for free.

The charge that connectionist nets are disadvantaged in explaining systematicity has generated a lot of interest. An often mentioned point of rebuttal (Aizawa 1997; Matthews 1997; Hadley 1997b) is that classical architectures do no better at explaining systematicity. There are also classical models that can be programmed to recognize ‘John loves Mary’ without being able to recognize ‘Mary loves John.’ The point is that neither the use of connectionist architecture alone nor the use of classical architecture alone enforces a strong enough constraint to explain pervasive systematicity. In both architectures, further assumptions about the nature of the processing must be made to ensure that ‘Mary loves John’ is also processed.

A discussion of this point should mention Fodor and McLaughlin's requirement that systematicity be explained as a matter of nomic necessity, that is as a matter of natural law. The complaint against connectionists is that while they may implement systems that exhibit systematicity, they will not have explained it unless it follows from their models as a nomic necessity. However, the demand for nomic necessity is a very strong one, and one that classical architectures clearly cannot meet either. So the only tactic for securing a telling objection to connectionists along these lines would be to weaken the requirement on the explanation of systematicity to one which classical architectures can and connectionists cannot meet. A convincing case of this kind has yet to be made.

As the systematicity debate has evolved, attention has been focused on defining the benchmarks that would answer Fodor and Pylyshyn's challenge. Hadley (1994a, 1994b) distinguishes three brands of systematicity. Connectionists have clearly demonstrated the weakest of these by showing that neural nets can learn to correctly recognize novel sequences of words (e.g., ‘Mary loves John’) that were not in the training set. However, Hadley claims that a convincing rebuttal must demonstrate strong systematicity, or better, strong semantical systematicity. Strong systematicity would require (at least) that ‘Mary loves John’ be recognized even if ‘Mary’ never appears in the subject position in any sentence in the training set. Strong semantical systematicity would require as well that the net show abilities at correct semantical processing of the novel sentences rather than merely distinguishing grammatical from ungrammatical forms. Niklasson and van Gelder (1994) have claimed success at strong systematicity, though Hadley complains that this is at best a borderline case. Hadley and Heyward (1997) tackle strong semantical systematicity, but by Hadley's own admission it is not clear that they have avoided the use of a classical architecture. Boden and Niklasson (2000) claim to have constructed a model that meets at least the spirit of strong semantical systematicity, but Hadley (2004) argues that even strong systematicity has not been demonstrated there. Whether one takes a positive or a negative view of these attempts, it is safe to say that no one has met the challenge of providing a neural net capable of learning complex semantical processing that generalizes to a full range of truly novel inputs.

Kent Johnson (2004) argues that the whole systematicity debate is misguided. Attempts at carefully defining the systematicity of language or thought leaves us with either trivialities or falsehoods. Connectionist surely have explaining to do, but Johnson recommends that it is fruitless to view their burden under the rubric of systematicity. What is needed instead is the development of neural net models capable of processing a language with a recursive syntax, which react immediately to the introduction of new items in the lexicon. The ‘systematicity’ debate may have already gone as Johnson advises, for what Hadley calls strong semantical systematicity seems a good measure of success in that direction.

8. Connectionism and Semantic Similarity

One of the attractions of distributed representations in connectionist models is that they suggest a solution to the problem of determining the meanings of brain states. The idea is that the similarities and differences between activation patterns along different dimensions of neural activity record semantical information. In this way, the similarity properties of neural activations provide intrinsic properties that fix meaning. However, Fodor and Lepore (1992, Ch. 6) challenge similarity based accounts on two fronts. The first problem is that human brains presumably vary significantly in the number of and connections between their neurons. Although it is straightforward to define similarity measures on two nets that contain the same number of units, it is harder to see how this can be done when the basic architectures of two nets differ. The second problem Fodor and Lepore cite is that even if similarity measures for meanings can be successfully crafted, they are inadequate to the task of meeting the desiderata which a theory of meaning must satisfy.

Churchland (1998) shows that the first of these two objections can be met. Citing the work of Laakso and Cottrell (2000) he explains how similarity measures between activation patterns in nets with radically different structures can be defined. Not only that, Laakso and Cottrell show that nets of different structures trained on the same task develop activation patterns which are strongly similar according to the measures they recommend. This offers hope that empirically well defined measures of similarity of concepts and thoughts across different individuals might be forged.

On the other hand, the development of a traditional theory of meaning based on similarity faces severe obstacles (Fodor and Lepore 1999), for such a theory would be required to assign sentences truth conditions based on an analysis of the meaning of their parts, and it is not clear that similarity alone is up to such tasks as fixing denotation in the way a standard theory demands. However, most connectionists who promote similarity based accounts of meaning reject many of the presupposition of standard theories. They hope to craft a working alternative which either rejects or modifies those presuppositions while still being faithful to the data on human linguistic abilities.

Calvo Garzon (2003) complains that there are reasons to think that connectionists must fail. Churchland's response has no answer to the collateral information challenge. That problem is that the measured similarities between activation patterns for a concept (say: grandmother) in two human brains are guaranteed to be very low because two people's (collateral) information on their grandmothers (name, appearance, age, character) is going to be very different. If concepts are defined by everything we know, then the measures for activation patterns of our concepts are bound to be far apart. This is a truly deep problem in any theory that hopes to define meaning by functional relationships between brain states. Philosophers of many stripes must struggle with this problem. Given the lack of a successfully worked out theory of concepts in either traditional or connectionist paradigms, it is only fair to leave the question for future research.

9. Connectionism and the Elimination of Folk Psychology

Another important application of connectionist research to philosophical debate about the mind concerns the status of folk psychology. Folk psychology is the conceptual structure that we spontaneously apply to understanding and predicting human behavior. For example, knowing that John desires a beer and that he believes that there is one in the refrigerator allows us to explain why John just went into the kitchen. Such knowledge depends crucially on our ability to conceive of others as having desires and goals, plans for satisfying them, and beliefs to guide those plans. The idea that people have beliefs, plans and desires is a commonplace of ordinary life; but does it provide a faithful description of what is actually to be found in the brain?

Its defenders will argue that folk psychology is too good to be false (Fodor 1988, Chapter 1). What more can we ask for the truth of a theory than that it provides an indispensable framework for successful negotiations with others? On the other hand, eliminativists will respond that the useful and widespread use of a conceptual scheme does not argue for its truth (Churchland 1989, Ch. 1). Ancient astronomers found the notion of celestial spheres useful (even essential) to the conduct of their discipline, but now we know that there are no celestial spheres. From the eliminativists point of view, an allegiance to folk psychology, like allegiance to folk (Aristotelian) physics, stands in the way of scientific progress. A viable psychology may require as radical a revolution in its conceptual foundations as is found in quantum mechanics.

Eliminativists are interested in connectionism because it promises to provide a conceptual foundation that might replace folk psychology. For example Ramsey et al. (1991) have argued that certain feed-forward nets show that simple cognitive tasks can be performed without employing features that could correspond to beliefs, desires and plans. Presuming that such nets are faithful to how the brain works, concepts of folk psychology fare no better than do celestial spheres. Whether connectionist models undermine folk psychology in this way is still controversial. There are two main lines of response to the claim that connectionist models support eliminativist conclusions. One objection is that the models used by Ramsey et al. are feed forward nets, which are too weak to explain some of the most basic features of cognition such as short term memory. Ramsey et al. have not shown that beliefs and desires must be absent in a class of nets adequate for human cognition. A second line of rebuttal challenges the claim that features corresponding to beliefs and desires are necessarily absent even in the feed forward nets at issue (Von Eckardt 2005).

The question is complicated further by disagreements about the nature of folk psychology. Many philosophers treat the beliefs and desires postulated by folk psychology as brain states with symbolic contents. For example, the belief that there is a beer in the refrigerator is thought to be a brain state that contains symbols corresponding to beer and a refrigerator. From this point of view, the fate of folk psychology is strongly tied to the symbolic processing hypothesis. So if connectionists can establish that brain processing is essentially non-symbolic, eliminativist conclusions will follow. On the other hand, some philosophers do not think folk psychology is essentially symbolic, and some would even challenge the idea that folk psychology is to be treated as a theory in the first place. Under this conception, it is much more difficult to forge links between results in connectionist research and the rejection of folk psychology.

Bibliography

Other Internet Resources

Related Entries

artificial intelligence | language of thought hypothesis | mental representation