R*(x,y)
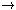
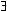 z[Rzy & R+(x,z)]
z[Rzy & R+(x,z)]
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
Fact 5 (R+):To prove this, we shall appeal to Fact 5 concerning the ancestral R* of R:
R*(x,y)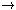
z[Rzy & R+(x,z)]
Fact 5 (R*):for any concept F and objects x and y:
[R*(x,y) &u(Rxu
Fu) & Her(F,R)]
Fy,
Now to prove Fact 5 (R+), assume R*(a,b). We want to show:
Notice that byz[Rzb & R+(a,z)]
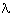 -Conversion, it suffices
to show:
-Conversion, it suffices
to show:
[Let us use ‘P’ to denote this concept under which (we have to show) b falls. Notice that we could prove Pb by instantiating Fact 5 (R*) to P, a, and b and establishing the antecedent of the result. In other words, by Fact (R*), we know:w
z[Rzw & R+(a,z)]b
[R*(a,b) &So if we can show the conjuncts of the antecedent, we are done. The first conjunct is already established, by hypothesis. So we have to show:u(Rau
Pu) & Her(P,R)]
Pb
(1)To see what we have to show for (1), we expand our defined notation and simplify by usingu(Rau
Pu)
(2) Her(P,R)
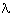 -Conversion. Thus, we
have to show:
-Conversion. Thus, we
have to show:
(1)So assume Rau, to show the consequent of (1). But it is an immediate consequence of the definition of the weak ancestral R+ that R+ is reflexive. (This is Fact 8 concerning the weak ancestral, in Section 4, "The Weak Ancestral of R".) So we may conjoin and conclude Rau & R+(a,a). From this, we may infer consequent of (1), by existential generalization, which is what we had to show.u[Rau
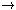
z(Rzu & R+(a,z))]
To show (2), we have to show that P is hereditary on R.
If we expand our defined notation and simplify by using
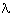 -Conversion), then we have to show:
-Conversion), then we have to show:
(2) RxySo assume[
z(Rzx & R+(a,z))
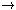
z(Rzy & R+(a,z))]
(A) Rxy &to show:z(Rzx & R+(a,z))
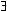 z(Rzy &
R+(a,z)). From the second conjunct
of (A), we know that there is some object, say d, such that:
z(Rzy &
R+(a,z)). From the second conjunct
of (A), we know that there is some object, say d, such that:
Rdx & R+(a,d); i.e.,So, by Fact 2 about the weak ancestral (Section 4, "The Weak Ancestral of R"), it follows that R*(a,x), from which it immediately follows that R+(a,x), by definition of R+. So, by appealing to the first conjunct of (A), we have:
R+(a,d) & Rdx
Rxy & R+(a,x),from which it follows that:
which is what we had to show.z(Rzy & R+(a,z)),
Return to Frege's Logic, Theorem, and Foundations for Arithmetic
| Edward N. Zalta zalta@stanford.edu |