This is a file in the archives of the Stanford Encyclopedia of Philosophy.

Proof of VC1

We exploit two mathematical facts about projection operators P_i:

(A) P_i² = P_i (the P_i are ‘idempotent’);

(B) If H is a Hilbert space of denumerable dimension, and if the P_i are operators projecting on q_i, where the set {q_i} forms an orthonormal basis of H, then _i P_i=I (where I is the identity operator) (the P_i form ‘a resolution of the identity’).

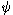Consider now an arbitrary state |> and an arbitrary nondegenerate operator Q on H3, its eigenvectors |q₁>, |q₂>, |q₃>, and projection operators P₁, P₂, P₃ whose ranges are the rays spanned by these vectors. The eigenvectors form an orthonormal basis, thus, by (B):

P₁ + P₂ + P₃ = I

Now, P₁, P₂, P₃ are compatible, so from assumption KS2 (a) (Sum Rule):

v(P₁) + v(P₂) + v(P₃) = v(I)

Now, from KS2 (b) (Product Rule) and (A):

	v(Pi)2 = v(Pi2) = v(Pi)
	v(Pi) = 1 or 0

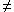Now, assume an observable R such that v(R) 0 in state |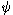>. From this assumption and KS2 (b) (Product Rule):

	v(R) = v(I R) = v(I) v(R)
	v(I) = 1

Hence:

(VC1)  v(P₁) + v(P₂) + v(P₃) = 1

where v(P_i) = 1 or 0, for i = 1, 2, 3.

Return to The Kochen-Specker Theorem

Copyright © 2000 by
Carsten Held <carsten.held@uni-erfurt.de>