Proof of the Falsification Theorem

Here we prove a version of the Falsification Theorem that only assumes condition-independence. In the following, if result-independence holds as well, all occurrences of ‘(c^k−1·e^k−1)’ may be dropped, which gives the theorem stated in the main text. If neither independence condition holds, the following proof still works, but with all occurrences of ‘c_k·(c^k−1·e^k−1)’ replaced by ‘cⁿ·e^k−1’ and with occurrences of ‘b·c^k−1’ replaced by ‘b·cⁿ’.

Theorem 1: The Falsification Theorem:
Suppose c^m, a subsequence of the whole evidence sequence cⁿ, consists of experiments or observations with the following property: whenever an outcome sequence e^k−1 of past conditions c^k−1 is deemed possible by both h_j·b and h_i·b, there are outcomes o_ku of the next condition c_k deemed impossible by h_j·b but deemed possible by h_i·b to at least some small degree δ. That is, suppose there is a δ > 0 such that for each c^k−1 and each of its outcome sequences e^k−1, if P[e^k−1 | h_i·b·c^k−1] > 0 and P[e^k−1 | h_j·b·c^k−1] > 0, then it is also the case that P[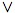 {o_ku:P[o_ku | h_j·b·c_k·(c^k−1·e^k−1)] = 0} | h_i·b·c_k·(c ^k−1·e^k−1)]  ≥  δ. Then,

P[{en : P[en | hj·b·c n]/P[en | hi·b·c n] = 0} | hi·b·c n]	=	P[{en : P[en | hj·b·c n] = 0} | hi·b·c n]
	≥	1−(1−δ)m, which approaches 1 for large m.

Proof

First notice that for each c_k from c^m,

(1−γ)	≥	P[u{oku : P[oku | hj·b·ck] > 0} | hi·b·ck·(c k−1·ek−1)]
	=	∑{oku∈Ok: P[oku | hj·b·ck] > 0} P[oku | hi·b·ck·(ck−1·e k−1)].

And for each c_k not from c^m,

P[_u{o_ku : P[o_ku | h_j·b·c_k] > 0} | h_i·b·c_k·(c ^k−1·e^k−1)]  = 1.

Then,

  P[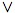{eⁿ : P[eⁿ | h_j·b·c ⁿ] > 0} | h_i·b·cⁿ]

	=	∑{en : P[en | hj·b·c n] > 0} P[en | hi·b·cn]
	=	∑{en−1: P[en−1 | hj·b·cn−1] > 0} (∑{onu∈On: P[onu | hj·b·cn·(cn−1·en−1)] > 0}  P[onu | hi·b·cn·(cn−1·en−1)]) · P[en−1 | hi·b·cn−1]
	=	∑{en−1: P[en−1 | hj·b·cn−1] > 0} P[u{onu : P[onu | hj·b·cn·(c n−1·en−1)] > 0} | hi·b·cn·(cn−1·en−1)] · P[en−1 | hi·b·cn−1]
	≤	(1−γ) · ∑{en−1: P[en−1 | hj·b·cn−1] > 0} P[en−1 | hi·b·cn−1]  if cn is from cm ,
or else
	=	∑{en−1: P[en−1 | hj·b·cn−1] > 0} P[en−1 | hi·b·c n−1]  if cn is not from cm;
…	≤	Πk=1m (1−γ)  =  (1−γ)m.

So,

P[{eⁿ : P[eⁿ | h_j·b·c ⁿ] = 0} | h_i·b·cⁿ] ≥  1 − (1−γ)ⁿ.

Also,

P[{eⁿ : P[eⁿ | h_j·b·cⁿ]/P[e ⁿ | h_i·b·cⁿ] = 0} | h_i·b·cⁿ] = P[{eⁿ : P[eⁿ | h_j·b·cⁿ] = 0} | h_i·b·cⁿ],

because

P[{eⁿ : P[eⁿ | h_j·b·cⁿ]/P[e ⁿ | h_i·b·cⁿ] > 0} | h_i·b·cⁿ]

=	∑{en: P[en | hj·b·cn]/P[e n | hi·b·cn] > 0} P[en | hi·b·cn]
=	∑{en: P[en | h j·b·cn] > 0 & P[en | hi·b·cn] > 0} P[en | hi·b·cn]
=	∑{en: P[en | h j·b·cn] > 0} P[en | hi·b·cn]
=	P[{en : P[en | hj·b·c n] > 0} | hi·b·cn].   □

[Back to Text]