Supplement to Relevance Logic
The Logic NR
Here is a Hilbert-style axiomatisation of the logic NR.
Our language contains propositional variables, parentheses, necessity, negation, conjunction, and implication. In addition, we use the following defined connectives:
AB =df ¬(¬A & ¬B)
A ↔ B =df (A → B) & (B → A)
| Axiom Scheme | Axiom Name | |
| 1. | A → A | Identity |
| 2. | (A → B) → ((B → C) → (A → C)) | Suffixing |
| 3. | A → ((A → B) → B) | Assertion |
| 4. | (A → (A → B)) → (A → B) | Contraction |
| 5. | (A & B) → A,(A & B) → B | & -Elimination |
| 6. | A → (A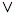 B), B → (A B), B → (A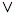 B) B) |
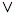 -Introduction -Introduction |
| 7. | ((A → B) & (A → B)) → (A → (B & C)) | & -Introduction |
| 8. | ((A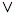 B) → C)↔((A → B) & (A → C)) B) → C)↔((A → B) & (A → C)) |
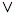 -Elimination -Elimination |
| 9. | (A & (B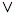 C)) → ((A & B) C)) → ((A & B)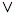 (A & C)) (A & C)) |
Distribution |
| 10. | (A → ¬B) → (B → ¬A) | Contraposition |
| 11. | ¬¬A → A | Double Negation |
| 12. | □(A → B) → (□A → □B) | K |
| 13. | (□A & □B) → □(A & B) | K& |
| Rule | Name |
A → B, A 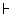 B B |
Modus Ponens |
A, B 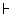 A & B A & B |
Adjunction |
A 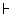 □A □A |
Necessitation |

