Supplement to Quantum Logic and Probability Theory
The Basic Theory of Ordering Relations
What follows is the briefest possible summary of the order-theoretic notions used in the main text. For a good introduction to this material, see Davey & Priestley [1990]. More advanced treatments can be found in Gratzer [1998] and Birkhoff [1967].- 1. Ordered sets
- 2. Lattices
- 3. Ortholattices
- 4. Orthomodularity
- 5. Closure Operators, Interior Operators and Adjunctions
1. Ordered Sets
A partial ordering -- henceforth, just an ordering -- on a set P is a reflexive, anti-symmetric, and transitive binary relation on P. Thus, for all p, q, r
∈ P,
we have
on P. Thus, for all p, q, r
∈ P,
we have
- p
 p
p
- p
 q and
q
q and
q p only if
p = q.
p only if
p = q.
- if p
 q
and q
q
and q r
then
p
r
then
p r
r
If
p q, we speak of p as
being less than, or below q, and of
q as being greater than, or above
p, in the ordering.
q, we speak of p as
being less than, or below q, and of
q as being greater than, or above
p, in the ordering.
A partially ordered set, or poset, is a pair
(P, ) where P is a set and
) where P is a set and
 is a specified ordering on
P. It is usual to let P denote both the set and the
structure, leaving
is a specified ordering on
P. It is usual to let P denote both the set and the
structure, leaving
 tacit wherever possible.
Any collection of subsets of some fixed set X, ordered by
set-inclusion, is a poset; in particular, the full power set
tacit wherever possible.
Any collection of subsets of some fixed set X, ordered by
set-inclusion, is a poset; in particular, the full power set
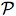 (X) is a poset under set inclusion.
(X) is a poset under set inclusion.
Let P be a poset. The meet, or greatest lower
bound, of p, q
∈ P, denoted by
p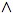 q,
is the greatest element of P -- if there is one -- lying below
both p and q. The join, or least upper
bound, of p and q, denoted by
p
q,
is the greatest element of P -- if there is one -- lying below
both p and q. The join, or least upper
bound, of p and q, denoted by
p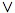 q,
is the least element of P -- if there is one -- lying above
both p and q. Thus, for any elements p,
q, r of P, we have
q,
is the least element of P -- if there is one -- lying above
both p and q. Thus, for any elements p,
q, r of P, we have
- if r
 p
p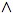 q,
then
r
q,
then
r p
and
r
p
and
r q
q
-
if p
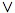 q
q
 r,
then
p
r,
then
p r
and
q
r
and
q r
r
Note that
p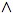 p =
p
p =
p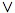 p =
p for all p in P. Note also that
p
p =
p for all p in P. Note also that
p q iff
p
q iff
p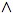 q = p iff
p
q = p iff
p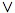 q = q.
q = q.
Note that if
the set P =
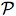 (X), ordered by
set-inclusion, then
p
(X), ordered by
set-inclusion, then
p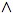 q =
p∩q
and
p
q =
p∩q
and
p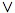 q =
p∪q.
However, if P is an arbitrary collection of subsets of
X ordered by inclusion, this need not be true. For instance,
consider the collection P of all subsets of
X = {1,2,...,n} having even cardinality.
Then, for instance,
{1,2}
q =
p∪q.
However, if P is an arbitrary collection of subsets of
X ordered by inclusion, this need not be true. For instance,
consider the collection P of all subsets of
X = {1,2,...,n} having even cardinality.
Then, for instance,
{1,2}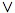 {2,3}
does not exist in P, since there is no
smallest set of 4 elements of X containing
{1,2,3}. For a different sort of example, let X be a vector
space and let P be the set of subspaces of
X. For subspaces M and N,
we have
{2,3}
does not exist in P, since there is no
smallest set of 4 elements of X containing
{1,2,3}. For a different sort of example, let X be a vector
space and let P be the set of subspaces of
X. For subspaces M and N,
we have
MN = M∩N, but M
N = span(M∪N).
The concepts of meet and join extend to infinite subsets of a poset
P. Thus, if
A⊆P, the meet of
A is the largest element (if any) below A, while
the join of A is the least element (if any) above
A. We denote the meet of A by
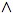 A or by
A or by
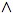 a∈A
a.
Similarly, the join of A is denoted by
a∈A
a.
Similarly, the join of A is denoted by
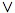 A or by
A or by
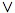 a∈A
a.
a∈A
a.
2. Lattices
A lattice is a poset
(L, )
in which every pair of elements has both a meet and a join. A
complete lattice is one in which every subset of
L has a meet and a join. Note that
)
in which every pair of elements has both a meet and a join. A
complete lattice is one in which every subset of
L has a meet and a join. Note that
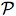 (X)
is a complete lattice with respect to set inclusion, as is the set of
all subspaces of a vector space. The set of finite subsets of an
infinite set X is a lattice, but not a complete lattice. The
set of subsets of a finite set having an even number of elements is an
example of a poset that is not a lattice.
(X)
is a complete lattice with respect to set inclusion, as is the set of
all subspaces of a vector space. The set of finite subsets of an
infinite set X is a lattice, but not a complete lattice. The
set of subsets of a finite set having an even number of elements is an
example of a poset that is not a lattice.
A lattice (L, ) is distributive
iff meets distribute over joins and vice versa:
) is distributive
iff meets distribute over joins and vice versa:
p(q
r) = (p
q)
(p
r), and
p
(q
r) = (p
q)
(p
r).
The power set lattice
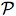 (X),
for instance, is distributive (as is any lattice of sets in which
meet and join are given by set-theoretic intersection and union). On
the other hand, the lattice of subspaces of a vector space is not
distributive, for reasons that will become clear in a moment.
(X),
for instance, is distributive (as is any lattice of sets in which
meet and join are given by set-theoretic intersection and union). On
the other hand, the lattice of subspaces of a vector space is not
distributive, for reasons that will become clear in a moment.
A lattice L is said to be bounded iff it contains a smallest element 0 and a largest element 1. Note that any complete lattice is automatically bounded. For the balance of this appendix, all lattices are assumed to be bounded, absent any indication to the contrary.
A complement for an element p of a (bounded) lattice
L is another element q such that p
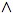 q = 0 and p
q = 0 and p
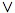 q = 1.
q = 1.
In the lattice
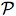 (X),
every element has exactly one complement, namely, its usual
set-theoretic complement. On the other hand, in the lattice of
subspaces of a vector space, an element will typically have infinitely
many complements. For instance, if L is the lattice of
subspaces of 3-dimensional Euclidean space, then a complement for a
given plane through the origin is provided by any line through the
origin not lying in that plane.
(X),
every element has exactly one complement, namely, its usual
set-theoretic complement. On the other hand, in the lattice of
subspaces of a vector space, an element will typically have infinitely
many complements. For instance, if L is the lattice of
subspaces of 3-dimensional Euclidean space, then a complement for a
given plane through the origin is provided by any line through the
origin not lying in that plane.
Proposition:
If L is distributive, an element of L can have at most one complement.Proof:
Suppose that q and r both serve as complements for p. Then, since L is distributive, we have
q = q 1
= q (p
r)
= (q p)
(q
r)
= 0 (q
r)
= q r
Hence, q
r. Symmetrically, we have r
q; thus, q = r.
Thus, no lattice in which elements have multiple complements is distributive. In particular, the subspace lattice of a vector space (of dimension greater than 1) is not distributive.
If a lattice is distributive, it may be that some of its
elements have a complement, while others lack a complement. A
distributive lattice in which every element has a complement is
called a Boolean lattice or a Boolean algebra. The
basic example, of course, is the power set
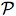 (X)
of a set X. More generally, any collection of subsets of
X closed under unions, intersections and complements is a
Boolean algebra; a theorem of Stone and Birkhoff tells us that, up to
isomorphism, every Boolean algebra arises in this way.
(X)
of a set X. More generally, any collection of subsets of
X closed under unions, intersections and complements is a
Boolean algebra; a theorem of Stone and Birkhoff tells us that, up to
isomorphism, every Boolean algebra arises in this way.
3. Ortholattices
In some non-uniquely complemented (hence, non-distributive) lattices, it is possible to pick out, for each element p, a preferred complement p′ in such a way that
- if p
 q
then
q′
q
then
q′
 p′
p′
- p′′ = p
 ,′)
an orthocomplemented lattice, or an ortholattice
for short.
,′)
an orthocomplemented lattice, or an ortholattice
for short.
Note again that if a distributive lattice can be orthocomplemented at all, it is a Boolean algebra, and hence can be orthocomplemented in only one way. In the case of L(H) the orthocomplementation one has in mind is M → M⊥ where M⊥ is defined as in Section 1 of the main text. More generally, if V is any inner product space (complete or not), let L(V) denote the set of subspaces M of V such that M = M⊥⊥ (such a subspace is said to be algebraically closed). This again is a complete lattice, orthocomplemented by the mapping M → M⊥.
4. Orthomodularity
There is a striking order-theoretic characterization of the lattice of
closed subspaces of a Hilbert space among lattices
L(V) of closed subspaces of more general
inner product spaces. An ortholattice L is said to be
orthomodular iff, for any pair p, q in L
with
p q,
q,
(OMI) (qp′)
p = q.
Note that this is a weakening of the distributive law. Hence, a Boolean lattice is orthomodular. It is not difficult to show that if H is a Hilbert space, then L(H) is orthomodular. The striking converse of this fact is due to Amemiya and Araki [1965]:
Theorem:
Let V be an inner product space (over R, C or the quaternions) such that L(V) is orthomodular. Then V is complete, i.e., a Hilbert space.
5. Closure Operators, Interior Operators and Adjunctions
Let P and Q be posets. A mapping
f : P
→
Q
is order preserving iff for all
p,q
∈
P, if
p q
then
f(p)
q
then
f(p) f(q).
f(q).
A closure operator on a poset P is an order-preserving map cl : P → P such that for all p ∈ P,
- cl(cl(p)) = p
- p
 cl(p).
cl(p).
Dually, an interior operator on P is an order-preserving mapping int : P → P on P such that for all p ∈ P,
- int(int(p)) = int(p)
- int(p)
 p
p
Elements in the range of cl are said to be closed; those in the range of int are said to be open. If P is a (complete) lattice, then the set of closed, respectively open, subsets of P under a closure or interior mapping is again a (complete) lattice.
By way of illustration, suppose that
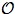 and
and
 are collections of subsets of a set X with
are collections of subsets of a set X with
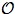 closed under arbitrary unions and
closed under arbitrary unions and
 under arbitrary intersections. For any set A
⊆
X, let
under arbitrary intersections. For any set A
⊆
X, let
cl(A) = ∩{C∈| A ⊆ C}, and
int(A) = ∪{O∈
| O ⊆ A}
Then cl and int are interior
operators on 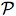 (X), for which the
closed and open sets are precisely
(X), for which the
closed and open sets are precisely
 and
and
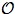 ,
respectively. The most familiar example, of course, is that in which
,
respectively. The most familiar example, of course, is that in which
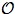 ,
,  are the open and closed subsets, respectively, of a topological
space. Another important special case is that in which
are the open and closed subsets, respectively, of a topological
space. Another important special case is that in which
 is the set of linear subspaces of a vector space V;
in this case, the mapping
span :
is the set of linear subspaces of a vector space V;
in this case, the mapping
span :  (V)
→
(V)
→
 (V)
sending each subset of V
to its span is a corresponding closure.
(V)
sending each subset of V
to its span is a corresponding closure.
An adjunction between two posets P and Q is an ordered pair (f, g) of mappings f : P → Q and g : Q → P connected by the condition that, for all p ∈ P, q ∈ Q
f(p)q if and only if p
g(q).
In this case, we call f a left adjoint for g, and call g a right adjoint for f. Two basic facts about adjunctions, both easily proved, are the following:
Proposition:
Let f : L → M be an order-preserving map between complete lattices L and M. Then
- f preserves arbitrary joins if and only if it has a right adjoint.
- f preserves arbitrary meets if and only if it has a left adjoint.
Proposition:
Let (f, g) be an adjunction between complete lattices L and M. Then
- g
f : L →L is a closure operator.
- f
g : M → M is an interior operator.

