Footnotes
1. Let I be
an interpretation function with respect to a model, so that
I(a) is the individual I assigns to the
individual constant `a', I(Fn)
is the n-place relation that I assigns to n-place
predicate Fn. Then for all n-place
predicates `Fn' and individuals constants
`c1', ..., `cn', the
sentence
`Fnc1...cn'
is true in the interpretation just in case <
I(c1), ...,
I(cn)> 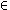 ext(I(Fn)). We would relativize
this clause to variable assignments in the usual way to define
satisfaction conditions for atomic sentences.
ext(I(Fn)). We would relativize
this clause to variable assignments in the usual way to define
satisfaction conditions for atomic sentences.
2. More
generally, if
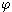 is a formula with free occurrences of exactly the
variables v1, ..., vn, then
`[
is a formula with free occurrences of exactly the
variables v1, ..., vn, then
`[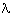 v1,...,
vn
v1,...,
vn 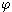 ]'
is an n-place complex predicate (normal quotation marks are
used here as stand-ins for quasi-quotation). In more complicated
applications we could allow
]'
is an n-place complex predicate (normal quotation marks are
used here as stand-ins for quasi-quotation). In more complicated
applications we could allow 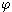 to contain no free
variables (in which case
`[
to contain no free
variables (in which case
`[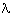
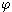 ]' denotes the
proposition that-
]' denotes the
proposition that-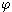 ) or more free variables
than are bound by the
) or more free variables
than are bound by the 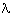 -operator (to allow
expressions like
`[
-operator (to allow
expressions like
`[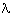 x Fxyz]', which we could
quantify into, as with
`
x Fxyz]', which we could
quantify into, as with
` y([
y([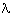 x Fxyz])'.
x Fxyz])'.
3. A standard sort of
comprehension schema
holds that for each open formula
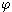 ,
,
 Xn
Xn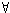 x1...
x1...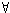 xn(Xnx1...xn
if and only if
xn(Xnx1...xn
if and only if 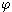 ).
).
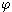 is a formula with free occurrences of exactly the
variables v1, ..., vn, then
`[
is a formula with free occurrences of exactly the
variables v1, ..., vn, then
`[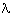 v1,...,
vn
v1,...,
vn 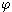 ]'
is an n-place complex predicate (normal quotation marks are
used here as stand-ins for quasi-quotation). In more complicated
applications we could allow
]'
is an n-place complex predicate (normal quotation marks are
used here as stand-ins for quasi-quotation). In more complicated
applications we could allow 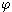 to contain no free
variables (in which case
`[
to contain no free
variables (in which case
`[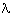
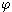 ]' denotes the
proposition that-
]' denotes the
proposition that-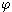 ) or more free variables
than are bound by the
) or more free variables
than are bound by the 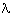 -operator (to allow
expressions like
`[
-operator (to allow
expressions like
`[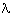 x Fxyz]', which we could
quantify into, as with
`
x Fxyz]', which we could
quantify into, as with
` y([
y([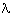 x Fxyz])'.
x Fxyz])'.
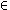 ext(I(Fn)). We would relativize
this clause to variable assignments in the usual way to define
satisfaction conditions for atomic sentences.
ext(I(Fn)). We would relativize
this clause to variable assignments in the usual way to define
satisfaction conditions for atomic sentences.
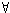 x1...
x1...