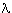 x (Px &
x (Px &| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
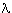 x (Px &
x (Px &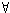 y((Py &
y((Py &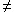 y)
y)

Now, there surely are some purely
qualitative individual essences, e.g., being smaller than every
other prime number. However, the only clear examples of such
belong to necessary beings like the number 2. The real question is
whether contingent beings have purely qualitative essences.
Adams [1979] has argued convincingly that they do not. His central
argument is that, given any possible world w, there is a world
Sym(w) that is "symmetrical" with respect to w. The
idea of symmetry here is difficult to define precisely, but the
intuitive idea is that Sym(w) contains two parts, each of
which is a sort of "copy" of w. One of these copies ---
call it C1 -- is (but for properties arising from the
existence of the other copy) identical to w in both
qualititative and nonqualitative respects, and in particular
contains exactly the same objectsas w. The other
copy --- call it C2 --- is an exact qualitative
replica of w, i.e., a copy that is indistinguishable from
w in all qualitative respects (other than those arising from
the existence of C1). Every object in C1, and hence in
w thus has a qualitative "doppelgänger" in C2,
an exact replica that has all of its purely qualitative properties.
Given this, it seems that there is a possible world
w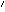 such that
Sym(w
such that
Sym(w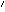 ) = Sym(w), but where now
w
) = Sym(w), but where now
w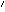 is identical with C2, and where
C1 is the replica. It follows that, for every possible world
w, there is another world w
is identical with C2, and where
C1 is the replica. It follows that, for every possible world
w, there is another world w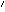 that
is qualitatively identical with w, but which contains only
doppelgängers of the objects in w.
that
is qualitatively identical with w, but which contains only
doppelgängers of the objects in w.
Now, one might argue that all that follows from the example is that,
for any object x and any world w containing x,
there is a distinct object y in some other world
w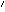 that has all of x's qualitative
nonmodal properties in w. That is, Adams' argument
from symmetrical worlds only makes plausible the idea that,
necessarily, every object x has, as one might say, a de
facto doppelgänger, something qualitatively identical to it
with regard to the properties it just happens to exemplify. It does
not follow that, necessarily, there is a complete, or
modal doppelgänger y of x, i.e., that,
for any world w in which x exists, there is a de
facto doppelgänger of x with respect to w
such that, in every other world w
that has all of x's qualitative
nonmodal properties in w. That is, Adams' argument
from symmetrical worlds only makes plausible the idea that,
necessarily, every object x has, as one might say, a de
facto doppelgänger, something qualitatively identical to it
with regard to the properties it just happens to exemplify. It does
not follow that, necessarily, there is a complete, or
modal doppelgänger y of x, i.e., that,
for any world w in which x exists, there is a de
facto doppelgänger of x with respect to w
such that, in every other world w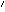 in
which x exists, there is a world
w
in
which x exists, there is a world
w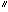 such that y is a de
facto doppelgänger in
w
such that y is a de
facto doppelgänger in
w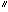 of x with respect to
w
of x with respect to
w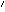 , and furthermore, that x is a
modal doppelgänger of y. Hence it does not follow that
there are no purely qualitative essences -- perhaps the purely
qualitative modal properties of x are sufficient to
distinguish it from any of its de facto doppelgängers,
i.e., that none of its de facto doppelgängers are modal
doppelgängers.
, and furthermore, that x is a
modal doppelgänger of y. Hence it does not follow that
there are no purely qualitative essences -- perhaps the purely
qualitative modal properties of x are sufficient to
distinguish it from any of its de facto doppelgängers,
i.e., that none of its de facto doppelgängers are modal
doppelgängers.
This is certainly a line worth pursuing. However, the central
problem with it is that there appears to be no intuitive
justification for this claim. Given that a doppelgänger
y in
w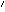 is qualititatively identical to
x with respect to the nonmodal properties x exemplifies
in w, what possible ground could there be for asserting that
the same couldn't to true of y with respect to any world in
which x exists? Intuitively, it seems, there are no such
grounds. A defender of this line would have to provide some.
is qualititatively identical to
x with respect to the nonmodal properties x exemplifies
in w, what possible ground could there be for asserting that
the same couldn't to true of y with respect to any world in
which x exists? Intuitively, it seems, there are no such
grounds. A defender of this line would have to provide some.
| Christopher Menzel cmenzel@tamu.edu |