(
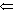 ) By Lemma 2.12,
) By Lemma 2.12, 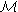 (
(  )
is common knowledge at
)
is common knowledge at
 , so E is common knowledge at
, so E is common knowledge at  by Proposition 2.4.
by Proposition 2.4.
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
Stanford Encyclopedia of Philosophy
Supplement to Common Knowledge
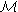 be the meet of the agents' partitions
be the meet of the agents' partitions
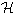 i
for each i
i
for each i
 N.
A proposition E
N.
A proposition E

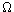 is common knowledge for the agents of N at
is common knowledge for the agents of N at
 iff
iff
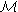 (
( )
)
 E.
In Aumann (1976), E is defined to be common knowledge at
E.
In Aumann (1976), E is defined to be common knowledge at
 iff
iff
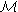 (
( )
)
 E.
E.
Proof.
(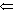 ) By Lemma 2.12,
) By Lemma 2.12, 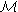 (
(  )
is common knowledge at
)
is common knowledge at
 , so E is common knowledge at
, so E is common knowledge at  by Proposition 2.4.
by Proposition 2.4.
(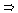 ) We must show that K *N ( E ) implies that
) We must show that K *N ( E ) implies that 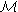 (
(  )
)  E.
Suppose that there exists
E.
Suppose that there exists 
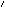

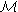 (
(  )
such that
)
such that 
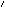
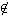 E.
Since
E.
Since 
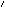

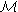 (
(  ),
),

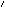 is reachable from
is reachable from  ,
so there exists a sequence 0, 1, . . . , m - 1 with associated states
,
so there exists a sequence 0, 1, . . . , m - 1 with associated states  1,
1,  2, . . . ,
2, . . . ,  m and information sets
m and information sets 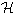 i k(
i k(  k ) such that
k ) such that  0 =
0 =  ,
,  m =
m = 
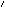 , and
, and  k
k 
 i k(
i k( k + 1). But at information set
k + 1). But at information set 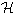 i k(
i k(  m ), agent i k does not know event E. Working backwards on k, we see that event E cannot be common knowledge, that is, agent i 1 cannot rule out the possibility that agent i 2 thinks that . . . that agent i m - 1 thinks that agent i m does not know E.
m ), agent i k does not know event E. Working backwards on k, we see that event E cannot be common knowledge, that is, agent i 1 cannot rule out the possibility that agent i 2 thinks that . . . that agent i m - 1 thinks that agent i m does not know E. 
| Peter Vanderschraaf peterv@MAIL1.ANDREW.CMU.EDU |