Stanford Encyclopedia of Philosophy
Supplement to Common Knowledge
Proof of Proposition 2.14
Proposition 2.14.
Let C*N be the greatest fixed
point of fE. Then
C*N(E) =
K*N(E).
Proof.
We have shown that
K*N(E) is a
fixed point of fE, so we only need to
show that
K*N(E) is
the greatest fixed point. Let B be a fixed point of
fB. We want to show that B
 KkN(E)
for each value
k
KkN(E)
for each value
k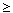 1.
We will proceed by induction on k. By hypothesis,
1.
We will proceed by induction on k. By hypothesis,
B = fE(B) =
K1N(E B)
B)
 K1N(E)
by monotonicity, so we have the k=1 case. Now suppose that for
k=m, B
K1N(E)
by monotonicity, so we have the k=1 case. Now suppose that for
k=m, B
 KmN(E).
Then by monotonicity,
KmN(E).
Then by monotonicity,
| (i) |
K1N(B)
 K1NK
mN(E) =
Km+1N(E)
K1NK
mN(E) =
Km+1N(E) |
We alo have:
| (ii) |
B =
K1N(E B) B)
 K1N(B)
K1N(B) |
by monotonicity, so combining (i) and (ii) we have:
B
 K1N(B)
K1N(B)
 Km+1N(E)
Km+1N(E)
completing the induction.

Return to Common Knowledge
Copyright © 2001, 2002
Supplement to Common Knowledge
Stanford Encyclopedia of Philosophy
 KkN(E)
for each value
k
KkN(E)
for each value
k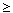 1.
We will proceed by induction on k. By hypothesis,
1.
We will proceed by induction on k. By hypothesis, KkN(E)
for each value
k
KkN(E)
for each value
k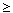 1.
We will proceed by induction on k. By hypothesis,
1.
We will proceed by induction on k. By hypothesis, B)
B)
 K1N(E)
K1N(E) KmN(E).
Then by monotonicity,
KmN(E).
Then by monotonicity,
K1NK mN(E) = Km+1N(E)
B)
K1N(B)
K1N(B)
Km+1N(E)
