Proof of Proposition 2.4

Proof.
If E F, then as we observed earlier, K_i(E) K_i(F), so

K 1N ( E ) =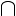

i N

K i( E ) =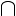

i N

Ki(F) = K1N(F)

If we now set E 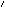= Kⁿ_N(E) and F 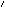= Kⁿ_N(F), then by the argument just given we have

Kn+1N(E) = K1N(E) K1N(F) = Kn+1N(F)

so we have m^th level mutual knowledge for every n 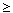1.

Hence if

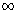
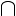
n = 1

KnN(E) then

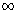
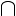
n = 1

KnN(F).

Return to Common Knowledge