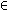 N,
N,
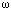
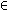 Ki1Ki2 … Kim(A)
Ki1Ki2 … Kim(A)
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
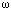
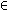 KmN(A)
iff
KmN(A)
iff
(1) For all agents i1, i2, … , imHence,N,
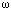
Ki1Ki2 … Kim(A)
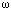
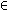 K*N(A)
iff (1) is the case for each m
K*N(A)
iff (1) is the case for each m
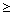 1.
1.
Proof.
Note first that
| ( 2 ) |
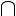
i 1 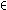 N N
|
K i 1 ( |
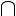
i 2 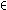 N N
|
K i 2 ( . . . ( |
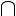
i m - 1 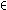 N N
|
K i m - 1 ( |
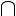
i m 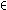 N N
|
K i m( A ) ) ) ) ) |
| = |
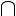
i 1 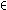 N N
|
K i 1 ( |
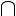
i 2 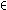 N N
|
K i 2 ( . . . ( |
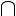
i m - 1 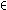 N N
|
K i m - 1 (K 1N ( A ) ) ) ) ) |
| = |
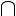
i 1 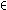 N N
|
K i 1 ( |
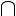
i 2 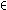 N N
|
K i 2 . . . ( |
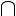
i m - 2 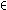 N N
|
K i m - 2 ( K 2N ( A ) ) ) ) |
| = . . . |
| = |
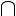
i 1 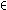 N N
|
K i 1( K m - 1N ( A ) ) |
| = | K mN ( A ) |
By ( 2 ), K mN ( A ) 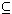 K i 1K i 2 . . . K i m( A )
for i 1, i 2, . . ., i m
K i 1K i 2 . . . K i m( A )
for i 1, i 2, . . ., i m 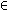 N
so if
N
so if 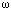
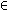 K mN ( A ) then condition ( 1 ) is satisfied. Condition ( 1 ) is equivalent to
K mN ( A ) then condition ( 1 ) is satisfied. Condition ( 1 ) is equivalent to
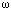
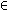
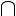
i 1N
K i 1 ( 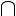
i 2N
K i 2 ( . . . ( 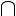
i m - 1N
K i m - 1 ( 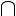
i mN
K i m ( A ) ) ) ) )
so by ( 2 ), if ( 1 ) is satisfied then 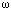
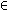 K mN ( A ).
K mN ( A ).

| Peter Vanderschraaf peterv@MAIL1.ANDREW.CMU.EDU |