Suppose that

 L*N ( E ).
By definition, there is a basis proposition A* such that
L*N ( E ).
By definition, there is a basis proposition A* such that 
 A*. It suffices to show that for each m
A*. It suffices to show that for each m 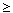 1 and for all agents i 1, i 2, . . . , i m
1 and for all agents i 1, i 2, . . . , i m  N,
N,
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
Stanford Encyclopedia of Philosophy
Supplement to Common Knowledge
 K*N (E),
that is, Lewis-common knowledge of E implies common
knowledge of E.
K*N (E),
that is, Lewis-common knowledge of E implies common
knowledge of E.
Proof.
Suppose that 
 L*N ( E ).
By definition, there is a basis proposition A* such that
L*N ( E ).
By definition, there is a basis proposition A* such that 
 A*. It suffices to show that for each m
A*. It suffices to show that for each m 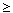 1 and for all agents i 1, i 2, . . . , i m
1 and for all agents i 1, i 2, . . . , i m  N,
N,

K i 1K i 2 . . . K i m( E )
We prove the result by induction on m. The m = 1 case follows at once from ( L1 ) and ( L3 ). Now if we assume that for m = k, 
 L*N ( E )
implies
L*N ( E )
implies 
 K i 1K i 2 . . . K i k( E ),
then L*N ( E )
K i 1K i 2 . . . K i k( E ),
then L*N ( E )  K i 1K i 2 . . . K i k( E )
because
K i 1K i 2 . . . K i k( E )
because  is an arbitrary possible world, so K i 1( A* )
is an arbitrary possible world, so K i 1( A* )  K i 1K i 2 . . . K i k( E )
by ( L3 ). Since ( L2 ) is the case and the agents of N are A*-symmetric reasoners,
K i 1K i 2 . . . K i k( E )
by ( L3 ). Since ( L2 ) is the case and the agents of N are A*-symmetric reasoners,
K i 1( A* ) K i 1K i 2 . . . K i k( E )
for any i k+1  N,
so
N,
so 
 K i 1K i 2 . . . K i k( E )
by ( L1 ), which completes the induction since i 1, i k+1, i 2, . . . , i k
are k + 1 arbitrary agents of N.
K i 1K i 2 . . . K i k( E )
by ( L1 ), which completes the induction since i 1, i k+1, i 2, . . . , i k
are k + 1 arbitrary agents of N. 
| Peter Vanderschraaf peterv@MAIL1.ANDREW.CMU.EDU |