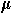 =
( =
( 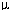 1, . . . , 1, . . . ,
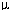 n ) n )

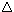 1 ( S - 1 )
x . . . x 1 ( S - 1 )
x . . . x
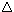 n ( S - n ) n ( S - n )
|
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
= (
1, . . . ,
n )

1 ( S - 1 ) x . . . x
n ( S - n )
are common knowledge. Then common knowledge of Bayesian rationality
is satisfied if, and only if,
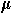 is an endogenous correlated equilibrium.
is an endogenous correlated equilibrium.
Proof.
Suppose first that common knowledge of Bayesian rationality is
satisfied. Then, by Proposition 3.4, for a given agent k
 N, if
N, if
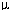 i( s k j ) > 0
for each agent i
i( s k j ) > 0
for each agent i
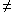 k,
then s k j must be optimal for k given some distribution
k,
then s k j must be optimal for k given some distribution
 k
k

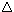 k ( S - k ).
Since the agents' distributions are common knowledge, this
distribution is precisely
k ( S - k ).
Since the agents' distributions are common knowledge, this
distribution is precisely
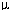 k ,
so ( 3.iii ) is satisfied for k. ( 3.iii ) is similarly
established for each other agent i
k ,
so ( 3.iii ) is satisfied for k. ( 3.iii ) is similarly
established for each other agent i
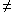 k, so
k, so
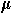 is an
endogenous correlated equilibrium.
is an
endogenous correlated equilibrium.
Now suppose that
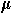 is an endogenous correlated equilibrium. Then, since the
distributions are common knowledge, ( 3.i ) is common knowledge, so
common knowledge of Bayesian rationality is satisfied by Proposition
3.4.
is an endogenous correlated equilibrium. Then, since the
distributions are common knowledge, ( 3.i ) is common knowledge, so
common knowledge of Bayesian rationality is satisfied by Proposition
3.4.
| Peter Vanderschraaf peterv@MAIL1.ANDREW.CMU.EDU |