Stanford Encyclopedia of Philosophy
Supplement to Common Knowledge
Rubinstein's Proof
[Note: See
Definition 3.2
for the notation used in this proof.]
Let T2 denote the
number of messages that Joanna's e-mail system sends, and
T1 denote the number of messages that Lizzi's
e-mail system sends. We might suppose that
Ti appears on each agent's computer
screen. If T1 = 0, then Lizzi sends no message,
that is,
 1
has occurred, in which case Lizzi's unique best response is to
choose A. If T2 = 0, then Joanna did
not receive a message. She knows that in this case, either
1
has occurred, in which case Lizzi's unique best response is to
choose A. If T2 = 0, then Joanna did
not receive a message. She knows that in this case, either
 1
has occurred and Lizzi did not send her a message, which occurs with
probability .51, or
1
has occurred and Lizzi did not send her a message, which occurs with
probability .51, or
 2
has occurred and Lizzi sent her a message which did not arrive,
which occurs with probability
.49
2
has occurred and Lizzi sent her a message which did not arrive,
which occurs with probability
.49 .
If
.
If  1
has occurred, then Lizzi is sure to choose A, so Joanna
knows that whatever Lizzi might do at
1
has occurred, then Lizzi is sure to choose A, so Joanna
knows that whatever Lizzi might do at
 2,
2,
| E(u2(A)
| T2=0) |
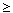 |
2(.51) + 0(.49)
.51 + .49 |
| |
> |
 4(.51)
+ 2(.49) 4(.51)
+ 2(.49)
.51 + .49 |
| |
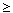 |
E(u2(B)
| T2=0 ) |
so Joanna is strictly better off choosing A no matter what Lizzi does
at either state of the world.
Suppose next that for all Ti < t,
each agents' unique best response given her expectations
regarding the other agent is A, so that the unique Nash
equilibrium of the game is (A,A). Assume that
T1 = t. Lizzi is uncertain whether
T2 = t, which is the case if Joanna
received Lizzi's tth automatic confirmation and
Joanna's tth confirmation was lost, or if
T2 = t
 1, which is the case if Lizzi's tth confirmation
was lost. Then
1, which is the case if Lizzi's tth confirmation
was lost. Then
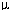 1(T2 =
t 1(T2 =
t 1
| T1 = t) 1
| T1 = t)
| = |
z
|
| |
= |

 +
(1 +
(1  ) ) |
| |
> |
½.[1] |
Thus it is more likely that Lizzi's last confirmation did not arrive
than that Joanna did receive this message. By the inductive
assumption, Lizzi assesses that Joanna will choose A if
T2 =
t 1.
So
1.
So
| E(u1(B) |
T1 = t) |
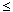 |
 4z +
2(1 4z +
2(1 z) z) |
| |
= |
 6z + 2 6z + 2 |
| |
< |
 3 + 2 3 + 2 |
| |
= |
 1, 1, |
and
E(u1(A) | T1
= t) = 0
since Lizzi knows that
 2 is the case. So
Lizzi's unique best action is A. Similarly, one can show
that A is Joanna's best reply if T2 =
t. So by induction, (A,A) is the unique
Nash equilibrium of the game for every t
2 is the case. So
Lizzi's unique best action is A. Similarly, one can show
that A is Joanna's best reply if T2 =
t. So by induction, (A,A) is the unique
Nash equilibrium of the game for every t
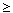 0.
0.
Return to Coordination and Common p-Belief
Copyright © 2001, 2002
Supplement to Common Knowledge
Stanford Encyclopedia of Philosophy
 1
has occurred, in which case Lizzi's unique best response is to
choose A. If T2 = 0, then Joanna did
not receive a message. She knows that in this case, either
1
has occurred, in which case Lizzi's unique best response is to
choose A. If T2 = 0, then Joanna did
not receive a message. She knows that in this case, either
 1
has occurred and Lizzi did not send her a message, which occurs with
probability .51, or
1
has occurred and Lizzi did not send her a message, which occurs with
probability .51, or
 2
has occurred and Lizzi sent her a message which did not arrive,
which occurs with probability
.49
2
has occurred and Lizzi sent her a message which did not arrive,
which occurs with probability
.49 .
If
.
If  1
has occurred, then Lizzi is sure to choose A, so Joanna
knows that whatever Lizzi might do at
1
has occurred, then Lizzi is sure to choose A, so Joanna
knows that whatever Lizzi might do at
 2,
2,
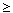
 4(.51)
+ 2(.49)
4(.51)
+ 2(.49)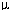 1(T2 =
t
1(T2 =
t