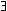 H(x =
H(x =
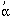 H
H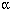 & H
& H
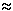 F)
F)
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
We can name this concept using ourH(x =
H
& H
F)
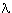 -notation as follows:
-notation as follows:
[Instead of writing out this lengthy expression being an x which is an extension of a concept equinumerous to F, let us abbreviate ourx
H(x =
H
& H
F)]
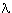 -notation for this concept as
‘F#’. Note that the extension of this concept,
-notation for this concept as
‘F#’. Note that the extension of this concept,
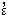 F#(
F#(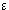 ), contains only extensions as members.
), contains only extensions as members.
Now Frege's explicit definition of ‘the number of Fs’ can be given as follows:
#F =dfThis definition identifies the number of Fs as the extension that contains all and only those extensions of concepts that are equinumerous to F.F#(
)
We can complete our preliminary work for the proof of Hume's Principle by formulating and proving the following Lemma (derived from Basic Law V), which simplifies the proof of Hume's Principle:
Lemma for Hume's Principle:This Lemma tells us that an extension such as
G
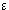
#F
G
F
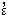 G
G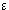 will be a
member of #F just in case G is equinumerous to F.
Clearly, since F is equinumerous to itself, it follows that
#F contains
will be a
member of #F just in case G is equinumerous to F.
Clearly, since F is equinumerous to itself, it follows that
#F contains
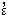 F
F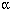 as a member.
From these facts, one can get a sense of how Frege derived Hume's
Principle Basic Law V in Gg. Here is a reconstruction of the
argument.
as a member.
From these facts, one can get a sense of how Frege derived Hume's
Principle Basic Law V in Gg. Here is a reconstruction of the
argument.
Proof of Hume's Principle from Basic Law V
Return to Frege's Logic, Theorem, and Foundations for Arithmetic
| Edward N. Zalta zalta@stanford.edu |