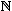 x & Precedes(y,x)
x & Precedes(y,x)
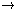
#[
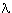 z Precedes+(z,y)] =
#[
z Precedes+(z,y)] =
#[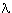 z Precedes+(z,x) & z
z Precedes+(z,x) & z 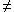 x]
x]
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
Lemma on Predecessor+:Now this Lemma can be proved with the help of the following Lemma:
x & Precedes(y,x)
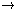
#[z Precedes+(z,y)] = #[
z Precedes+(z,x) & z
x]
Lemma: No Number Ancestrally Precedes Itself
x[
x
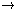
Precedes*(x,x)]
(Proof) [Exercise for the Reader]
Now to prove the Lemma on Predecessor+, assume that
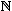 n and Precedes(m,n).
We want to show:
n and Precedes(m,n).
We want to show:
#[By Hume's Principle, it suffices to show:z Precedes+(z,m)] = #[
z Precedes+(z,n) & z
n]
[Now it is a fact about equinumerosity (see the Facts About Equinumerosity, in §3, Equinumerosity, Fact 1) that if two concepts are materially equivalent, then they are equinumerous. It therefore suffices to show thatz Precedes+(z,m)]
[
z Precedes+(z,n) & z
n]
And byx([
z Precedes+(z,m)]x
[
z Precedes+(z,n) & z
n]x)
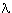 -Conversion, it suffices to show:
-Conversion, it suffices to show:
So let us pick an arbitrary object, say a, and show:x[Precedes+(x,m)
Precedes+(x,n) & x
n]
Precedes+(a,m)Precedes+(a,n) & a
n
(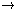 ) Assume
Precedes+(a,m). Then from our
assumption that Precedes(m,n) and a Fact about
R+ (see §4, Weak Ancestral, Facts
About R+, Fact 2), it follows that
Precedes*(a,n). A fortiori, then,
Precedes+(a,n). Now by the Lemma
mentioned at the outset of this proof, namely, No Natural Number
Ancestrally Precedes Itself, we know that
) Assume
Precedes+(a,m). Then from our
assumption that Precedes(m,n) and a Fact about
R+ (see §4, Weak Ancestral, Facts
About R+, Fact 2), it follows that
Precedes*(a,n). A fortiori, then,
Precedes+(a,n). Now by the Lemma
mentioned at the outset of this proof, namely, No Natural Number
Ancestrally Precedes Itself, we know that
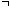 Precedes*(n,n).
Since a ancestrally precedes n and n does not, it
follows that a
Precedes*(n,n).
Since a ancestrally precedes n and n does not, it
follows that a 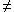 n. We have
therefore proved what we were after, namely:
n. We have
therefore proved what we were after, namely:
Precedes+(a,n) & a(n
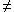 n. By definition, the first
conjunct tells us that either Precedes*(a,n) or
a = n. Since we know by assumption that the latter
disjunct is not true, we know Precedes*(a,n).
But from this fact, the fact that Predecessor is 1-1, and our
assumption that Precedes(m,n), it follows from a
fact about R+ (see §4, Weak Ancestral, Facts
About R+, Fact 7), that
Precedes+(a,m), which is what we had
to show.
n. By definition, the first
conjunct tells us that either Precedes*(a,n) or
a = n. Since we know by assumption that the latter
disjunct is not true, we know Precedes*(a,n).
But from this fact, the fact that Predecessor is 1-1, and our
assumption that Precedes(m,n), it follows from a
fact about R+ (see §4, Weak Ancestral, Facts
About R+, Fact 7), that
Precedes+(a,m), which is what we had
to show.
Return to Proof that Q is Hereditary on the Natural Numbers
| Edward N. Zalta zalta@stanford.edu |