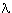 y Precedes(y,#[
y Precedes(y,#[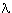 z Precedes+(z,y)])]0
z Precedes+(z,y)])]0
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
[Byy Precedes(y,#[
z Precedes+(z,y)])]0
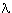 -Conversion, it suffices to show:
-Conversion, it suffices to show:
Precedes(0, #[So, by the definition of Predecessor, we have to show that there is a concept F and object x such that:z Precedes+(z,0)])
(1) FxWe can demonstrate that there is an F and x for which (1), (2) and (3) hold if we pick F to be [
(2) #[z Precedes+(z,0)] = #F
(3) 0 = #[u Fu & u
x]
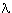 z
Precedes+(z,0)] and pick x to be 0.
We now establish (1), (2), and (3) for these choices.
z
Precedes+(z,0)] and pick x to be 0.
We now establish (1), (2), and (3) for these choices.
To show that (1) holds, we have to show:
[But we know, from the definition of Precedes+, that Precedes+(0,0), So by abstraction usingz Precedes+(z,0)]0
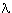 -Conversion, we are done.
-Conversion, we are done.
To show that (2) holds, we need do no work, since our choice of F requires us to show:
#[which we know by the logic of identity.z Precedes+(z,0)] = #[
z Precedes+(z,0)],
To show (3) holds, we need to show:
(A) 0 = #[[Note that theu Precedes+(u,0) & u
0]
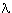 -expression in (A) has been
simplified by applying
-expression in (A) has been
simplified by applying
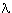 -Conversion to the following (which, strictly
speaking, is what results when you substitute our choice for F
in (3)):
-Conversion to the following (which, strictly
speaking, is what results when you substitute our choice for F
in (3)):
[In what follows, we use the simplified version of thisu [
z Precedes+(z,0)]u & u
0]
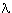 -expression.]
-expression.]
To show (A), it suffices to show the following, in virtue of the Lemma Concerning Zero (in our subsection on The Concept Natural Number in §4):
And byx ([
u Precedes+(u,0) & u
0]x)
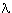 -Conversion, it suffices to show:
-Conversion, it suffices to show:
(B)We establish (B) as follows.x (Precedes+(x,0) & x
0)
When we established Theorem 2 (i.e., the fact that 0 is not the successor of any number), we proved that nothing precedes 0:
From this, and Fact (3) about R* (in the subsection on the Ancestral of R, in §4), it follows that nothing ancestrally precedes 0:x Precedes(x,0)
Now suppose (for reductio) the negation of (B); i.e, that there is some object, say a, such that Precedes+(a,0) and ax Precedes*(x,0)
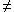 0. Then, by definition of
Precedes+, it follows that either
Precedes*(a,0) or a = 0. But since
our reductio hypthesis includes that
a
0. Then, by definition of
Precedes+, it follows that either
Precedes*(a,0) or a = 0. But since
our reductio hypthesis includes that
a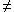 0, it must be that
Precedes*(a,0), which contradicts the fact
displayed immediately above.
0, it must be that
Precedes*(a,0), which contradicts the fact
displayed immediately above.
Return to Frege’s Logic, Theorem, and Foundations for Arithmetic
| Edward N. Zalta zalta@stanford.edu |