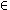
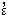 (
(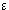 + 22
= 5)
+ 22
= 5)
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
1 + 22 = 5one can prove that
1For it follows from our premise (by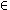
(
+ 22 = 5)
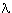 -Abstraction) that:
-Abstraction) that:
[Independently, by the logic of identity, we know:z z + 22 = 5]1
So we may conjoin this fact and the result of([
z z + 22 = 5]
) =
([
z z + 22 = 5]
)
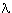 -Abstraction to produce:
-Abstraction to produce:
Then, by existential generalization on the concept [([
z z + 22 = 5]
) =
([
z z + 22 = 5]
) & [
z z + 22 = 5]1
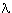 z z + 22 = 5],
it follows that:
z z + 22 = 5],
it follows that:
By the definition of membership, we obtain:G[
([
z z + 22 = 5]
) =
G
& G1]
1And, finally, by our Rewrite Rule, we establish what we set out to prove: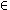
([
z z + 22 = 5]
)
1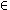
(
+ 22 = 5)
Return to Frege's Logic, Theorem, and Foundations for Arithmetic
| Edward N. Zalta zalta@stanford.edu |