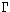 1 are separated by an
angle
1 are separated by an
angle
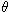 with 0
with 0
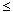
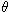
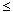 sin -1 (1/3), then
sin -1 (1/3), then
 1
is realizable.
1
is realizable.
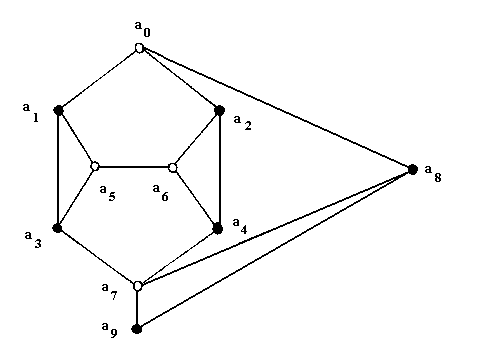
Figure 4: Ten-point KS graph
 1
1
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
We now show (see Kochen and Specker 1967: , Redhead 1987: 126):
If vectors u(a0) and u(a9), corresponding to points a0 and a9 of the following ten-point KS graphSuppose that1 are separated by an angle
with 0
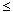
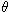
sin -1 (1/3), then
1 is realizable.
Figure 4: Ten-point KS graph1
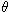 , the angle between
u(a0) and u(a9), is any acute angle. Since
u(a8) is orthogonal to u(a0) and
u(a9), and u(a7) also is orthogonal to
u(a9), u(a7) must lie in the plane defined by
u(a0) and u(a9). Moreover, the direction of
u(a7) can be chosen such that, if
, the angle between
u(a0) and u(a9), is any acute angle. Since
u(a8) is orthogonal to u(a0) and
u(a9), and u(a7) also is orthogonal to
u(a9), u(a7) must lie in the plane defined by
u(a0) and u(a9). Moreover, the direction of
u(a7) can be chosen such that, if
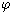 is the angle between u(a0)
and u(a7), then
is the angle between u(a0)
and u(a7), then
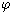 =
=
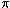 /2
/2 
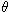 .
.
Now, let u(a5) = i and u(a6) = k and choose a third vector j such that i, j, k form a complete set of orthonormal vectors. Then u(a1), being orthogonal to i, may be written as:
u(a1) = (j + xk) (1 + x2) -1/2for a suitable real number x, and similarly u(a2), being orthogonal to k, may be written as:
u(a2) = (i + yj) (1 + y2) -1/2for a suitable real number y. But now the orthogonality relations in the diagram yield:
u(a3) = u(a5) × u(a1) = (-xj + k) (1 + x2) -1/2Now, u(a0) is orthogonal to u(a1) and u(a2), so:u(a4) = u(a2) × u(a6) = (yi
j) (1 + y2) -1/2
u(a0) = u(a1) × u(a2) / ( | u(a1) × u(a2) | ) = (-xyi + xjSimilarly, u(a7) is orthogonal to u(a3) and u(a4), so:k) (1 + x2 + x2 y2) -1/2
u(a7) = u(a4) × u(a3) / ( | u(a4) × u(a3) | ) = (-iRecalling now that the inner product of two unit vectors just equals the cosine of the angle between them, we get:yj
xyk) (1 + y2 + x2 y2) -1/2
u(a0) u(a7) = cosThus:= xy[(1 + x2 + x2 y2) (1 + y2 + x2 y2)] -1/2
sinThis expression achieves a maxium value of 1/3 for x = y == xy[(1 + x2 + x2 y2) (1 + y2 + x2 y2)] -1/2
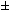 1. Hence, the diagram is
realizable, if 0
1. Hence, the diagram is
realizable, if 0
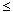
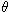
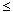 sin-1(1/3),
or, equivalently if 0
sin-1(1/3),
or, equivalently if 0
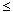 sin
sin 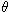
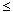 1/3.
1/3.
Return to The Kochen-Specker Theorem
| Carsten Held cheld@ruf.uni-freiburg.de |