Stanford Encyclopedia of Philosophy
Notes to Infinitary Logic
Notes
1. Observe, however,
that while the formation rules for
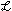 (
( ,
,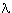 )
allow the deployment of infinitely many quantifiers, each preformula
can contain only finitely many alternations of
quantifiers. Languages permitting infinite quantifier alternations
have been developed in the literature, but we shall not discuss them
here.
)
allow the deployment of infinitely many quantifiers, each preformula
can contain only finitely many alternations of
quantifiers. Languages permitting infinite quantifier alternations
have been developed in the literature, but we shall not discuss them
here.
2. This remark loses
its force when the base language contains predicate symbols with
infinitely many argument places. However, this possibility is
excluded here since our base language is a conventional first-order
language.
3. I.e., such that no
contradictions can be derived from
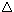 using the deductive machinery in
P.
using the deductive machinery in
P.
4. If A is a
set,
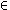 | A denotes the membership
relation on A, i.e., {<x, y>
| A denotes the membership
relation on A, i.e., {<x, y>
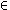 A
× A: x
A
× A: x
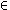 y}.
y}.
5. Strictly speaking,
this is only the case when
 is regular, that is, not the limit of
<
is regular, that is, not the limit of
<  cardinals each of which is
<
cardinals each of which is
<  . In view of the fact that "most"
cardinals are regular, we shall take this as read.
. In view of the fact that "most"
cardinals are regular, we shall take this as read.
6. It should be pointed
out, however, that there are languages
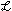 (
( ,
,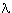 )
apart from
)
apart from
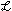 (
( ,
, )
and
)
and 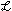 (
( 1,
1, )
which are complete; for example, all languages
)
which are complete; for example, all languages
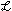 (
( +,
+, )
and
)
and 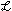 (
(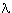 ,
,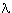 )
with inaccessible
)
with inaccessible 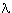 .
.
7. This is just a
consequence of the fact that a first-order deduction is a finite
sequence, hence a member of
H( ).
).
8. Take
 to be any logically false sentence!
to be any logically false sentence!
9. A set
A is transitive if x
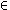 y
y 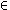 A
A
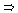 x
x 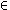 A.
A.
10. For the
definition of admissible set, see the Supplement at the end of
§5.
Copyright © 2000
Notes to Infinitary Logic
Stanford Encyclopedia of Philosophy
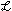 (
( ,
,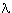 )
allow the deployment of infinitely many quantifiers, each preformula
can contain only finitely many alternations of
quantifiers. Languages permitting infinite quantifier alternations
have been developed in the literature, but we shall not discuss them
here.
)
allow the deployment of infinitely many quantifiers, each preformula
can contain only finitely many alternations of
quantifiers. Languages permitting infinite quantifier alternations
have been developed in the literature, but we shall not discuss them
here.
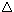 using the deductive machinery in
P.
using the deductive machinery in
P.
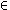 | A denotes the membership
relation on A, i.e., {<x, y>
| A denotes the membership
relation on A, i.e., {<x, y>
 ,
, to be any logically false sentence!
to be any logically false sentence!
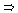 x
x