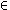 A, then {a, b}
A, then {a, b}
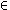 A and
A and
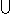 A
A 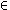 A;
A;
(ii) if a
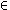 A and X
A and X
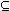 A is
A is
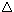 0 on A, then
X
0 on A, then
X  a
a
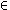 A;
A;
(iii) if a
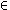 A, X
A, X
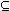 A is
A is
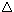 0 on A, and
0 on A, and
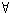 x
x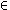 a
a y(<x,y>
y(<x,y>
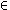 X), then, for some b
X), then, for some b
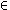 A,
A,
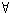 x
x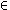 a
a y
y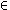 b(<x,y>
b(<x,y>
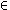 X).
X).
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
(i) if a, bCondition (ii) -- theA, then {a, b}
A and
A
A;
(ii) if a
A and X
A is
0 on A, then X
a
A;
(iii) if a
A, X
A is
0 on A, and
x
a
y(<x,y>
X), then, for some b
A,
x
a
y
b(<x,y>
X).
 0-separation
scheme -- is a restricted version of Zermelo's axiom of
separation. Condition (iii) -- a similarly weakened version of the
axiom of replacement -- may be called the
0-separation
scheme -- is a restricted version of Zermelo's axiom of
separation. Condition (iii) -- a similarly weakened version of the
axiom of replacement -- may be called the
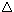 0-replacement scheme.
0-replacement scheme.
It is quite easy to see that if A is a transitive set such
that <A,
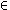 | A> is a model of
ZFC, then A is admissible. More generally,
the result continues to hold when the power set axiom is omitted
from ZFC, so that both
H(
| A> is a model of
ZFC, then A is admissible. More generally,
the result continues to hold when the power set axiom is omitted
from ZFC, so that both
H( ) and
H(
) and
H( 1) are
admissible. However, since the latter is uncountable, the Barwise
compactness theorem fails to apply to it.
1) are
admissible. However, since the latter is uncountable, the Barwise
compactness theorem fails to apply to it.
| John L. Bell jbell@julian.uwo.ca |