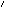 from Qd to Qb. There
are now 2 sub-subcases to consider.
from Qd to Qb. There
are now 2 sub-subcases to consider.
| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
2. One might wish to understand the probabilistic relations stated in this principle as a definition of what a common cause is. However, this is not a plausible idea. For, consider a case in which A1 is a common cause of A2 and A3, while A2 in its turn causes A4, and A3 in its turn causes A5, where A4 and A5 are simultaneous. In this case A4 and A5 will typically be uncorrelated conditional upon A2 (assuming that A2 is the only cause of A4). Moreover, an occurrence of A2 will typically make an occurrence of A4 more likely, and, typically, it will make an occurrence of A5 more likely. Thus A2 would count as a common cause of A4 and A5 if the above probabilistic relations were a definition of what it is to be a common cause. But by assumption A2 is not a cause of A5, and thus not a common cause of A4 and A5. Thus the probabilistic relations that are used to state Reichenbach's principle of the common cause should not be regarded as a definition of what a common cause is.
3. Qk is an indirect cause of Qp exactly when there is a chain of direct causes starting at Qk and ending at Qp. Qp is an effect of Qk iff Qk is a cause of Qp iff Qk is a direct or indirect cause of Qp.
4. Let me explain how this follows from the Markov condition using terminology and theorems from Spirtes, Glymour and Scheines 1993, chapter 3. Let us call a quantity Qc a ‘forking path common cause’ of quantities Qa and Qb if and only if there exists a path that always goes causally downstream from Qc to Qa, a path that always goes causally downstream from Qc to Qb, and these paths do not have any vertices other than Qc in common. Let us now conditionalize on all the forking path common causes of Qa and Qb. Claim: Every path from Qa to Qb will then be inactive. (Paths here are assumed not to contain any vertex more than once.) Let me indicate how to prove this claim.
If such a path P starts at Qa going causally downstream,
then it will at some point have to switch to going causally upstream,
since Qa is not a cause of Qb. It will thus
contain a collider. This collider will be inactive since we are not
conditionalizing on it nor on any quantity that is a descendent of
it, since we are conditionalizing only on quantities that are
causally upstream from Qa. (I am assuming that the graphs
are not cyclical.) Thus such a path P will be inactive. Now consider
any path P from Qa to Qb that starts at
Qa going causally upstream. There must be some point
Qc at which point P first starts going causally downstream
(since Qb is not a cause of Qa). There are two
possibilities: P keeps going causally downstream all the way until it
reaches Qb, or it reaches a collider Qd where P
switches back to going causally upstream again. In the first case,
Qc is a common cause of Qa and
Qb. So we have conditionalized on it, so P is inactive. In
the second case, Qd is a collider. There are then 2
subcases: Qd does not lie causally upstream from a forking
path common cause of Qa and Qb, or it does. If
Qd does not lie causally upstream from a common cause,
then it does not lie upstream from a quantity that is conditionalized
upon, so the collider is inactive, so P is inactive. If Qd
does lie causally upstream from a forking path common cause of
Qa and Qb, then there must be a downstream path
P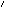 from Qd to Qb. There
are now 2 sub-subcases to consider.
from Qd to Qb. There
are now 2 sub-subcases to consider.
Sub-subcase i: P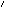 has no vertices in common with
the part of path P that lies between Qa and
Qc. In that case, Qc is a forking path common
cause of Qa and Qb: to go downstream from
Qc to Qa, follow the part of P that lies
between Qc and Qa;to go downstream from
Qc to Qb (without intersecting the path to
Qa), first take the part of P that lies between
Qc and Qd, and then follow P
has no vertices in common with
the part of path P that lies between Qa and
Qc. In that case, Qc is a forking path common
cause of Qa and Qb: to go downstream from
Qc to Qa, follow the part of P that lies
between Qc and Qa;to go downstream from
Qc to Qb (without intersecting the path to
Qa), first take the part of P that lies between
Qc and Qd, and then follow P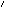 to Qb. So in this case we have
conditionalized upon Qc on P, so P is inactive.
to Qb. So in this case we have
conditionalized upon Qc on P, so P is inactive.
Sub-subcase ii: every downstream path P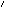 from
Qd to Qb intersects somewhere with the part of
P that lies between Qa and Qc. Take some such
P
from
Qd to Qb intersects somewhere with the part of
P that lies between Qa and Qc. Take some such
P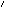 , and consider the furthest point Qe
downstream along P
, and consider the furthest point Qe
downstream along P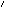 at which
P
at which
P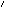 intersects with P between Qa and
Qc. Such a Qe must be a forking path common
cause of Qa and Qb: follow P to get to
Qa, follow P
intersects with P between Qa and
Qc. Such a Qe must be a forking path common
cause of Qa and Qb: follow P to get to
Qa, follow P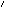 to get to
Qb. Thus we have conditionalized upon Qe which
lies on P. Thus P is inactive.
to get to
Qb. Thus we have conditionalized upon Qe which
lies on P. Thus P is inactive.
Thus any path P from Qa to Qb must be inactive once we have conditionalized upon all forking path common causes. Thus Qa and Qb are independent conditional upon a subset of all common causes of Qa and Qb.
5. The law of conditional independence is not violated by this type of case.
6.
Let me sketch a proof. Any probability distribution that is allowed
by the independence condition can be generated as follows. Assign
some probability distribution over all the determinants outside S. By
assumption this must be a probability distribution that is jointly
independent, i.e. a product of distributions for each such
determinant. Now first look at the set S1 of quantities in
S that have no direct causes in S. The probability distribution over
these quantities will be determined by the distribution of their
determinants outside S, and hence be a jointly independent
distribution. Now look at the set S2 of quantities all of
whose direct causes in S are in S1. The probability
distribution over any quantity S2 is obtained by
multiplying the probability distributions of its direct causes in
S1 with the probability distribution of its determinant
outside S. (At least, this is so if all distinct values of direct
causes of Q in S and determinants of Q outside S, determine distinct
values of Q. This may not be so, but this does not affect the
independence claims that I am making here.) And let us continue in
this way with S3, .... until we have a distribution over
all quantities in S. The only correlations in the joint distribution
over quantities in S that will now occur will be between causes and
their effects, and between the effects of a common cause. For
consider any quantities Q1 and Q2 that are not
so related. They will have no ‘ultimate inputs’ (the determinants
outside S that determine the values of these quantities) in common,
so the sets of ‘ultimate inputs’ for Q1 and ‘ultimate
inputs’ for Q2 are independent, which entails that
Q1 and Q2 are themselves independent. Moreover,
the correlations between any two quantities Q1 and
Q2 that are not related as cause and effect will disappear
when one conditionalizes upon the direct causes of one of them, say
Q1. For the only remaining input into Q1 is
independent of anything other than effects of Q1. So
Q1 is independent of anything other than effects of
Q1 conditional upon the direct causes of
Q1. Hence, the causal Markov condition holds.
| Frank Arntzenius arntzeni@rci.rutgers.edu |