Stanford Encyclopedia of Philosophy
Supplement to Common Knowledge
Proof of Proposition 3.11
Proposition 3.11 (Aumann 1987)
If each agent i
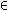 N is
N is
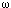 -Bayes rational at each possible world
-Bayes rational at each possible world
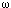
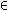
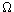 , then the agents are following
an Aumann correlated equilibrium. If the CPA is satisfied, then
the correlated equilibrium is objective.
, then the agents are following
an Aumann correlated equilibrium. If the CPA is satisfied, then
the correlated equilibrium is objective.
Proof.
We must show that
s :
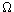
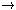 S
as defined by the
S
as defined by the
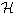 i-measurable
s i's of the Bayesian rational agents is an objective
Aumann correlated equilibrium. Let i
i-measurable
s i's of the Bayesian rational agents is an objective
Aumann correlated equilibrium. Let i
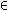 n and
n and
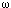
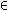
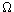 be given, and let
g i :
be given, and let
g i :
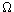
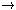 S i
be any function that is a function of s i. Since s
i is constant over each cell of
S i
be any function that is a function of s i. Since s
i is constant over each cell of
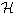 i , g i
must be as well, that is, g i is
i , g i
must be as well, that is, g i is
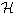 i-measurable.
By Bayesian rationality,
i-measurable.
By Bayesian rationality,
E ( u i
 s | s |
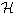 i )( i )(
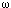 ) )
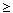 E ( u i ( g i , s - i )|
E ( u i ( g i , s - i )|
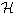 i )( i )(
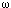 ) )
|
Since
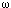 was chosen arbitrarily, we can take iterated expectations to get
was chosen arbitrarily, we can take iterated expectations to get
E ( E ( u i
 s | s |
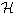 i )( i )(
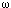 ) ) ) )
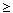 E ( E ( u i ( g i , s - i )|
E ( E ( u i ( g i , s - i )|
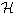 i )( i )(
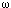 ) ) ) )
|
which implies that
E ( u i
 s ) s )
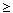 E ( u i ( g i , s - i ) ) E ( u i ( g i , s - i ) )
|
so s is an Aumann correlated equilibrium.
Return to Common Knowledge
Supplement to Common Knowledge
Stanford Encyclopedia of Philosophy
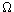
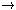 S
as defined by the
S
as defined by the
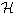 i-measurable
s i's of the Bayesian rational agents is an objective
Aumann correlated equilibrium. Let i
i-measurable
s i's of the Bayesian rational agents is an objective
Aumann correlated equilibrium. Let i
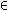 n and
n and
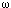
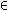
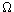 be given, and let
g i :
be given, and let
g i :
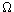
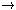 S i
be any function that is a function of s i. Since s
i is constant over each cell of
S i
be any function that is a function of s i. Since s
i is constant over each cell of
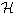 i , g i
must be as well, that is, g i is
i , g i
must be as well, that is, g i is
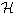 i-measurable.
By Bayesian rationality,
i-measurable.
By Bayesian rationality,
 s |
s |
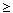 E ( u i ( g i , s - i )|
E ( u i ( g i , s - i )|