Supplement to Common Knowledge
Proof of Lemma 2.16
Lemma 2.16.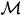 (ω)
is common
knowledge for the agents of N at ω.
(ω)
is common
knowledge for the agents of N at ω.
Proof.
Since
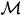 is a coarsening of
is a coarsening of
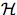 i for
each i ∈ N,
Ki(
i for
each i ∈ N,
Ki(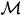 (ω)).
Hence,
K1N(
(ω)).
Hence,
K1N(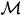 (ω) ), and since by definition
Ki(
(ω) ), and since by definition
Ki(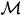 (ω)) =
{ ω |
(ω)) =
{ ω |
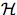 i(ω)
⊆
i(ω)
⊆
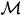 (ω)}
=
(ω)}
=
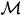 (ω),
(ω),
K1N( (ω)) =
∩
i ∈ NKi( (ω)) =
(ω)
Applying the recursive definition of mutual knowledge, for any m ≥ 1,
KmN( (ω)) =
∩
i ∈ NKi(Km−1N( (ω)) =
∩
i ∈ NKi( (ω)) =
(ω)
so, since ω ∈
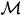 (ω),
by definition we have ω ∈
K*N(
(ω),
by definition we have ω ∈
K*N(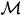 (ω)).
(ω)).

Copyright © 2007 by
Peter Vanderschraaf <pvanderschraaf@gmail.com>
Giacomo Sillari <gsillari@sas.upenn.edu>
Peter Vanderschraaf <pvanderschraaf@gmail.com>
Giacomo Sillari <gsillari@sas.upenn.edu>

