Stability Concepts in Evolutionary Games
Logical relations among concepts of stability used in discussions of
the EPD and other evolutionary games are established in a series of
papers by Bendor and Swistak. Some conditions on game payoffs and some
conditions on the course of evolution are described below. Logical
relations among these conditions are represented in the diagram that
follows.
Conditions on payoffs
(
V(
i,
j) is the total payoff that
i
gets playing against
j.)
| CS |
Axelrod (“Collective Stability”) |
∀j[V(i,i) ≥
V(j,i)] |
| MS |
Maynard Smith |
∀j[V(i,i) >
V(j,i) or
(V(i,i)=V(j,i)
& V(i,j) >
V(j,j))] |
| BL |
Boyd and Lorberbaum |
∀j[V(i,i) >
V(j,i) or
(V(i,i)=V(j,i)
& ∀k(V(i,k) ≥
V(j,k)))] |
| BS |
Bendor and Swistak |
∀j[V(i,i) >
V(j,i) or
(V(i,i)=V(j,i)
& V(i,j) ≥
V(j,j))] |
Conditions on the course of evolution
u and
r (“universal” and
“restricted”) indicates that the condition obtains under
any rule of evolution or merely under the replication
dynamics.
s and
w (“strong” and
“weak”) indicate that the strategy eradicates invasions or
merely survives them.
n and
b (“narrow”
and “broad”) indicate that the invaders are homogeneous
(i.e., they all employ the same strategy), or heterogeneous. For
example
i has
uwb (universal weak broad) stability
if, under any rule of evolution, it survives sufficiently small
heterogeneous invasions.
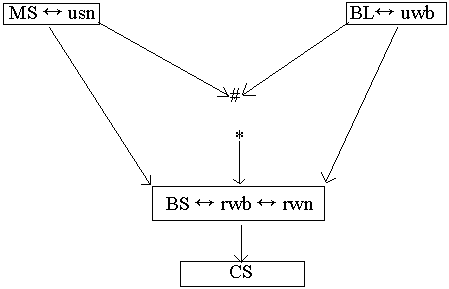
Relations among stability conditions
Logical implications are indicated by chains of arrows (and by
relative vertical position). Conditions stronger than # cannot be
satisfied by any EPD and conditions weaker than * are satisfied by
EPDs with all levels of cooperation from 0% to 100%.
Return to Prisoner's Dilemma Entry


