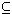 KkN(E)
for each value
k
KkN(E)
for each value
k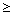 1.
We will proceed by induction on k. By hypothesis,
1.
We will proceed by induction on k. By hypothesis,| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
Proof.
We have shown that
K*N(E) is a
fixed point of fE, so we only need to
show that
K*N(E) is
the greatest fixed point. Let B be a fixed point of
fB. We want to show that B
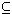 KkN(E)
for each value
k
KkN(E)
for each value
k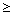 1.
We will proceed by induction on k. By hypothesis,
1.
We will proceed by induction on k. By hypothesis,
 B)
B)
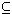 K1N(E)
K1N(E)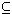 KmN(E).
Then by monotonicity,
KmN(E).
Then by monotonicity,
We alo have:
(i) K1N(B) K1NK mN(E) = Km+1N(E)
by monotonicity, so combining (i) and (ii) we have:
(ii) B = K1N(E B)
K1N(B)
Bcompleting the induction.K1N(B)
Km+1N(E)

First published: June 12, 2002
Content last modified: June 12, 2002