Prior's Modal Logic
One of the first philosophical logicians to think about these
problems was Arthur Prior. He pointed out that SQML is "haunted by the
myth that whatever exists exists necessarily" ([1968], p. 48). His
goal was to develop a modal logic for contingent beings (see Prior
[1957] and [1967]). Prior developed a solution to these problems by
rejecting the interdefinability of the ‘necessity’ and
‘possibility’ operators and restricting the Rule of
Necessitation. The central notion that underlies Prior's system is the
notion of necessary statability. Prior's idea is that when
a is a contingent being, then propositions about a
are not even statable in a world where a doesn't exist; i.e.,
such propositions are not necessarily statable. Intuitively, only
those formulas which are about necessary beings or which are wholly
general in character are necessarily statable. Thus, Prior introduces
the modal claim
S to indicate that the proposition denoted
by
to indicate that the proposition denoted
by
 is necessarily statable.
is necessarily statable.
Prior then undermines the interdefinability of possibility and
necessity by distinguishing ‘not possibly false’ from
‘necessarily true’ as follows. Using the operator
‘ ’ as primitive, Prior labels any
statement
’ as primitive, Prior labels any
statement
 for which there is no world where it is false as
‘not possibly false’ (i.e.,
for which there is no world where it is false as
‘not possibly false’ (i.e.,
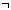

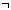
 ).
For example, when a is a contingent being, the statement
‘Pa
).
For example, when a is a contingent being, the statement
‘Pa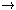 Pa’ is not possibly false,
since there is no world in which the statement is false. However,
since this statement will be neither true nor false (but rather
unstatable) at worlds where a doesn't exist, it is not a
‘necessarily true’ statement in the full or strong sense
of being true in every possible world. Prior defines this strong sense
of necessity in his object language in terms of possibility and
statability as follows:
Pa’ is not possibly false,
since there is no world in which the statement is false. However,
since this statement will be neither true nor false (but rather
unstatable) at worlds where a doesn't exist, it is not a
‘necessarily true’ statement in the full or strong sense
of being true in every possible world. Prior defines this strong sense
of necessity in his object language in terms of possibility and
statability as follows:
 is necessarily true iff
is necessarily true iff
 is necessarily statable and
is necessarily statable and
 is not possibly false. In formal terms:
is not possibly false. In formal terms:


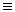 S
S &
&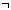

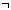

So, when a is a contingent being,
‘Pa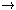 Pa’ is not a necessary truth. But when
‘a’ denotes an object that necessarily exists,
‘Pa
Pa’ is not a necessary truth. But when
‘a’ denotes an object that necessarily exists,
‘Pa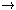 Pa’ will be necessarily
true. Also, completely general sentences like
‘
Pa’ will be necessarily
true. Also, completely general sentences like
‘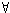 xPx
xPx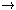
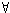 xPx’
will be necessarily true.
xPx’
will be necessarily true.
Given this distinction between weak necessity (‘not possibly
false’) and strong necessity, Prior must make sure that the Rule
of Necessitation never allows us to infer the strong necessity of a
theorem of logic that is only weakly necessary. Thus, for Prior, the
Rule of Necessitation must be reformulated as follows:
Revised RN: If 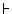
 , then
, then
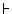 (S
(S
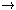

 )
)
Thus, after establishing that
Pa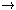 Pa is a theorem of logic, we cannot infer that
Pa is a theorem of logic, we cannot infer that
 (Pa
(Pa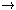 Pa). However, we can
infer that
Pa). However, we can
infer that
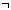

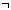 (Pa
(Pa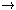 Pa),
since Prior does accept the following rule of inference:
Pa),
since Prior does accept the following rule of inference:
If 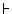
 , then
, then
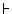
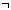

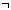

It is now easy to see that BF, NE, and CBF are no longer theorems of
Prior's logic. The proof of BF relied both on the interdefinability of
possibility and necessity as well as on the unrevised Rule of
Necessitation. (Specifically, the interdefinability of possibility and
necessity plays a role behind the scenes in the second line of the
second subproof in the
derivation of BF, and
the Rule of Necessitation was used in line 2 in the third subproof and
in line 2 of the final, assembled proof of BF.) The proof of NE is
undermined since it relied on unrevised RN as well. (Specifically,
Revised RN will not permit the inference on line 3 of the
derivation of NE.) Finally, the proof of CBF
cannot proceed in the usual way using Revised RN. (Specifically, we
cannot appeal to Revised RN on line 2 of the
derivation of CBF.)
Since BF, NE, and CBF are no longer theorems, one might think that
Prior had succeeded in finding the correct modal logic for
actualism. However, few actualists have adopted this logic. The
interdefinability of possibility and necessity has seemed just too
elegant to abandon---it seems to capture something deep about the
logical relationships among our modal beliefs. Actualists are divided
on the queston of Prior's restriction on RN---some see it as
unnecessary while others accept some such weakening of RN. Probably
the most awkward consequence of Prior's logic, however, is the
fact that logical contradictions which aren't necessarily
statable turn out to be weakly possible! Before we explain why this is
so, note that when a is a contingent being, the claim
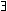 y(y = a) is not possibly false ---
it is true at any world where a exists, and is neither true
nor false at worlds where a fails to exist. As Deutsch
observes, "Yet surely there is a sense in which ‘Prior
[a] exists’ might have been false; and there is
no way to express this in Prior's system" ([1990], 92-93). Prior
here would emphasize that this weak necessity of a's
existence doesn't contradict the fact that a is a
contingent being, for the fact that a is contingent is
properly expressed by the fact that neither
y(y = a) is not possibly false ---
it is true at any world where a exists, and is neither true
nor false at worlds where a fails to exist. As Deutsch
observes, "Yet surely there is a sense in which ‘Prior
[a] exists’ might have been false; and there is
no way to express this in Prior's system" ([1990], 92-93). Prior
here would emphasize that this weak necessity of a's
existence doesn't contradict the fact that a is a
contingent being, for the fact that a is contingent is
properly expressed by the fact that neither
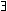 y(y = a) nor its negation are
necessarily true (since neither is necessarily statable). However, if
that is what it is to say that a fact is contingent, then any literal
contradiction mentioning a will be contingent! For example,
the contradiction Pa &
y(y = a) nor its negation are
necessarily true (since neither is necessarily statable). However, if
that is what it is to say that a fact is contingent, then any literal
contradiction mentioning a will be contingent! For example,
the contradiction Pa &
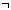 Pa is
not necessarily true, nor is its negation, since neither is statable
in a world where a doesn't exist. So this contradiction
becomes a contingent claim. Indeed, if we suppose that
Pa is
not necessarily true, nor is its negation, since neither is statable
in a world where a doesn't exist. So this contradiction
becomes a contingent claim. Indeed, if we suppose that
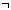

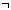
 (using Prior's defined sense of
(using Prior's defined sense of
 ) defines a weak
sense in which
) defines a weak
sense in which
 is possibly true, it turns out that both the
formulas
is possibly true, it turns out that both the
formulas
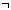
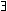 y(y =
a) and the contradictory formula Pa &
y(y =
a) and the contradictory formula Pa &
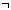 Pa are possibly true in exactly this sense. As
I have put it elsewhere ([1991], 348), Prior's modal logic "cannot
distinguish the expression of [a's] contingency from the
possibility of manifest repugnancies".
Pa are possibly true in exactly this sense. As
I have put it elsewhere ([1991], 348), Prior's modal logic "cannot
distinguish the expression of [a's] contingency from the
possibility of manifest repugnancies".
Supplement to Actualism
Stanford Encyclopedia of Philosophy
 ’ as primitive, Prior labels any
statement
’ as primitive, Prior labels any
statement
 for which there is no world where it is false as
‘not possibly false’ (i.e.,
for which there is no world where it is false as
‘not possibly false’ (i.e.,
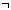

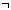
 ).
For example, when a is a contingent being, the statement
‘Pa
).
For example, when a is a contingent being, the statement
‘Pa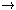 Pa’ is not possibly false,
since there is no world in which the statement is false. However,
since this statement will be neither true nor false (but rather
unstatable) at worlds where a doesn't exist, it is not a
‘necessarily true’ statement in the full or strong sense
of being true in every possible world. Prior defines this strong sense
of necessity in his object language in terms of possibility and
statability as follows:
Pa’ is not possibly false,
since there is no world in which the statement is false. However,
since this statement will be neither true nor false (but rather
unstatable) at worlds where a doesn't exist, it is not a
‘necessarily true’ statement in the full or strong sense
of being true in every possible world. Prior defines this strong sense
of necessity in his object language in terms of possibility and
statability as follows:
 is necessarily true iff
is necessarily true iff
 is necessarily statable and
is necessarily statable and
 is not possibly false. In formal terms:
is not possibly false. In formal terms:

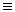 S
S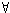 xPx
xPx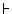
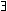 y(y = a) is not possibly false ---
it is true at any world where a exists, and is neither true
nor false at worlds where a fails to exist. As Deutsch
observes, "Yet surely there is a sense in which ‘Prior
[a] exists’ might have been false; and there is
no way to express this in Prior's system" ([1990], 92-93). Prior
here would emphasize that this weak necessity of a's
existence doesn't contradict the fact that a is a
contingent being, for the fact that a is contingent is
properly expressed by the fact that neither
y(y = a) is not possibly false ---
it is true at any world where a exists, and is neither true
nor false at worlds where a fails to exist. As Deutsch
observes, "Yet surely there is a sense in which ‘Prior
[a] exists’ might have been false; and there is
no way to express this in Prior's system" ([1990], 92-93). Prior
here would emphasize that this weak necessity of a's
existence doesn't contradict the fact that a is a
contingent being, for the fact that a is contingent is
properly expressed by the fact that neither