Proof of Proposition 3.12
Proposition 3.12 (Bicchieri 1993)
In an extensive form game of perfect information, the agents follow
the backwards induction solution if the following conditions are
satisfied for each agent i at each information set I ik:
- i is rational, i knows this and i knows the game, and
- At any information set I jk+ 1 that immediately follows
I ik, i knows at I ik what j knows at I jk+ 1.
Proof.
The proof is by induction on m, the number of potential moves in the
game. If m = 1, then at I i1, by (a) agent i chooses a
strategy which yields i her maximum payoff, and this is the backwards
induction solution for a game with one move.
Now suppose the proposition holds for games having at most m = r
potential moves. Let
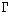 be a game of perfect information with r + 1 potential moves, and suppose that
(
be a game of perfect information with r + 1 potential moves, and suppose that
( 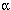 ) and
(
) and
( 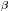 ) are satisfied at every node of
) are satisfied at every node of
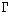 . Let I i1 be the
information set corresponding to the root of the tree for
. Let I i1 be the
information set corresponding to the root of the tree for
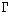 . At I i1, i knows that
(a) and
(b) obtain for each of the subgames that start at the information
sets which immediately follow I i1. Then i knows that the
outcome of play for each of these subgames is the backwards induction
solution for that subgame. Hence, at I i1 i's payoff
maximizing strategy is a branch of the tree starting from I
i1 which leads to a subgame whose backwards induction solution
is best for i, and since i is rational, i chooses such a branch at
I i1. But this is the backwards induction solution for
the entire game
. At I i1, i knows that
(a) and
(b) obtain for each of the subgames that start at the information
sets which immediately follow I i1. Then i knows that the
outcome of play for each of these subgames is the backwards induction
solution for that subgame. Hence, at I i1 i's payoff
maximizing strategy is a branch of the tree starting from I
i1 which leads to a subgame whose backwards induction solution
is best for i, and since i is rational, i chooses such a branch at
I i1. But this is the backwards induction solution for
the entire game
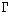 , so the proposition is proved for
m = r + 1.
, so the proposition is proved for
m = r + 1.
Return to Common Knowledge
Supplement to Common Knowledge
Stanford Encyclopedia of Philosophy
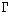 be a game of perfect information with r + 1 potential moves, and suppose that
(
be a game of perfect information with r + 1 potential moves, and suppose that
( 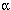 ) and
(
) and
( 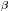 ) are satisfied at every node of
) are satisfied at every node of
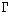 . Let I i1 be the
information set corresponding to the root of the tree for
. Let I i1 be the
information set corresponding to the root of the tree for
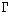 . At I i1, i knows that
(a) and
(b) obtain for each of the subgames that start at the information
sets which immediately follow I i1. Then i knows that the
outcome of play for each of these subgames is the backwards induction
solution for that subgame. Hence, at I i1 i's payoff
maximizing strategy is a branch of the tree starting from I
i1 which leads to a subgame whose backwards induction solution
is best for i, and since i is rational, i chooses such a branch at
I i1. But this is the backwards induction solution for
the entire game
. At I i1, i knows that
(a) and
(b) obtain for each of the subgames that start at the information
sets which immediately follow I i1. Then i knows that the
outcome of play for each of these subgames is the backwards induction
solution for that subgame. Hence, at I i1 i's payoff
maximizing strategy is a branch of the tree starting from I
i1 which leads to a subgame whose backwards induction solution
is best for i, and since i is rational, i chooses such a branch at
I i1. But this is the backwards induction solution for
the entire game
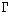 , so the proposition is proved for
m = r + 1.
, so the proposition is proved for
m = r + 1.