Finite Fields as Models for Euclidean Plane Geometry
Finite Fields
A field is a set F equipped with two operations +,
 such that
such that
- the pair <F,+> is a group, i.e.,
| + is closed: |
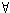 x,y x,y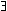 z(x
+ y = z) z(x
+ y = z) |
| + is associative: |
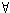 x,y,z(x +
(y + z) = (x + y) + z) x,y,z(x +
(y + z) = (x + y) + z) |
| there is a neutral element: |
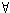 x(x + 0 = x) x(x + 0 = x) |
| every element has an inverse: |
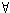 x x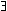 y(x
+ y = y + x = 0) y(x
+ y = y + x = 0) |
- likewise <F,
 >
is a group, the neutral element being 1
>
is a group, the neutral element being 1
- the following distributivity laws hold:
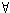 x,y,z(x
x,y,z(x
 (y + z) = (x
(y + z) = (x
 y) + (y
y) + (y
 z))
z))
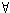 x,y,z((x + y)
x,y,z((x + y)
 z) = (x
z) = (x
 z) + (y
z) + (y
 z))
z))
It is straightforward to see that the real numbers
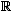 with the usual addition and multiplication is a field. In this case
the set F is infinite, but F can be finite as
well. Then we have a finite field or a Galois field. There is however
one very important distinction between a field such as
with the usual addition and multiplication is a field. In this case
the set F is infinite, but F can be finite as
well. Then we have a finite field or a Galois field. There is however
one very important distinction between a field such as
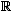 and a Galois field. In the latter, given the multiplicative neutral
element 1, there is a prime number p such that
p
and a Galois field. In the latter, given the multiplicative neutral
element 1, there is a prime number p such that
p 1 =
0. p is called the characteristic of the field. It can be
shown that if p is the characteristic of a field, then it must
have pn elements, for some natural number
n. In addition Galois fields are the only finite fields.
1 =
0. p is called the characteristic of the field. It can be
shown that if p is the characteristic of a field, then it must
have pn elements, for some natural number
n. In addition Galois fields are the only finite fields.
Example: the Galois field with characteristic 3 and number of
elements 3, GF(3) for short.
The tables for addition and multiplication tell the whole story:
| + |
0 |
1 |
2 |
| 0 |
0 |
1 |
2 |
| 1 |
1 |
2 |
0 |
| 2 |
2 |
0 |
1 |
 |
0 |
1 |
2 |
| 0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
| 2 |
0 |
2 |
1 |
In the first case, 1 + 1 + 1 = 0.
It is easy to see that the above tables correspond to addition and
multiplication modulo p. In other words, in the field a =
b if and only if a
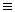 b (mod p).
b (mod p).
Euclidean Axioms in a Finite Field
To see how a finite field can be a model, I will take the incidence
relation. The axioms for the incidence relation are:
- Through two points exactly one straight line can be drawn.
- There are at least two points on every straight line.
- There are at least three points that are not on the same straight
line.
In case we take GF(3) as a possible model, then to a point
p corresponds to a couple (x,y), such that
0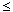 x,y
x,y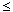 2.
A line corresponds to a triple
(a,b,c), such that
0
2.
A line corresponds to a triple
(a,b,c), such that
0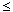 a,b,c
a,b,c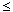 2
and at most one of a = 0 or b = 0, or, equivalently,
at most one of
a
2
and at most one of a = 0 or b = 0, or, equivalently,
at most one of
a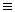 0 or
b
0 or
b 0 (mod 3). The incidence
relation is translated as follows: a point p lies on a line
A iff if (x,y) corresponds to p and
(a,b,c) corresponds to A, then the
equation ax+by+c = 0 is satisfied, or,
equivalently,
ax+by+c
0 (mod 3). The incidence
relation is translated as follows: a point p lies on a line
A iff if (x,y) corresponds to p and
(a,b,c) corresponds to A, then the
equation ax+by+c = 0 is satisfied, or,
equivalently,
ax+by+c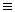 0
(mod 3) is satisfied. Some facts are now straightforward to check:
0
(mod 3) is satisfied. Some facts are now straightforward to check:
- There are exactly p2 points.
- There are exactly p(p+1) straight lines.
- On every straight line there are exactly p points.
- Through every point pass exactly p+1 straight lines.
- The axioms (a), (b) and (c) are true in this model.
A graphical representation could look like this:
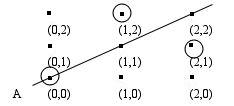
The line indicated by A corresponds to x =
y. This seems to correspond nicely to the classical Euclidean
case. However something strange happens with the linear equation
x + y = 0. In the drawing the 3 points that are on
this line have been circled. As must be clear these lines are “bad”
and should be "ignored" in the model.
In order to satisfy the remaining axioms further restrictions are
required on the size of the domain. These will just be mentioned
without details:
- p must have the specific form 4n+3 (and not
4n+1).
- p must in addition have the specific form
8mq1q2...qk
 1,
where qi is the i-th odd prime (so
q1 = 3) and m a positive integer.
1,
where qi is the i-th odd prime (so
q1 = 3) and m a positive integer.
The second condition that is needed to guarantee the existence of
the Euclidean "kernel" is a non-trivial statement. It actually
requires some essential parts of number theory to prove that there
are prime numbers of that form. There are, classically speaking, an
infinite number of them. By choosing p large enough, one can
make the ‘kernel’ as large as one desires to have the
Euclidean approximation as close as one wants.
Note: As Ernst Welti points out, it would be a rather
annoying situation for a finitist if the proof that shows that there
are an infinite number of primes of the right form were not
finitistically acceptable. Although the original proof of Dirichlet
was in fact unacceptable, fortunately there does now exist a
finitistically acceptable proof of the theorem.
Return to Finitism in Geometry
Supplement to Finitism in Geometry
Stanford Encyclopedia of Philosophy
x,y
z(x + y = z)
x,y,z(x + (y + z) = (x + y) + z)
x(x + 0 = x)
x
y(x + y = y + x = 0)
 >
is a group, the neutral element being 1
>
is a group, the neutral element being 1
x,y,z(x
(y + z) = (x
y) + (y
z))
x,y,z((x + y)
z) = (x
z) + (y
z))
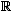 with the usual addition and multiplication is a field. In this case
the set F is infinite, but F can be finite as
well. Then we have a finite field or a Galois field. There is however
one very important distinction between a field such as
with the usual addition and multiplication is a field. In this case
the set F is infinite, but F can be finite as
well. Then we have a finite field or a Galois field. There is however
one very important distinction between a field such as
 b (mod p).
b (mod p). 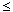 x,y
x,y
 1,
where qi is the i-th odd prime (so
q1 = 3) and m a positive integer.
1,
where qi is the i-th odd prime (so
q1 = 3) and m a positive integer.