Proof of VC2
Let Sx, Sy,
Sz be the usual angular momentum operators
satisfying [Sx, Sy] =
i Sz, and define S2
:= Sx2 +
Sy2 +
Sz2. It can be shown that the
eigenvalues of S2 are s(s + 1) where s is an integer or
half-integer.
Now let s=1. Then it follows (see e.g. Kochen and Specker 1967: 308,
Redhead 1987: 37-38) that Sx2,
Sy2,
Sz2 are all mutually commuting and
that:
Sx2 +
Sy2 +
Sz2 = 2I,
where I is the identity operator. Now, from KS2 (a) (Sum Rule):
v(Sx2) +
v(Sy2) +
v(Sz2) = 2v(I)
Now, assume an observable R such that v(R)
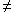 0 in state
|
0 in state
|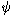 >. From this
assumption and KS2 (b) (Product Rule):
>. From this
assumption and KS2 (b) (Product Rule):
| |
v(R) = v(I R) = v(I) v(R) |
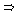 |
v(I) = 1 |
Hence:
(VC2)
v(Sx2) +
v(Sy2) +
v(Sz2) = 2
where v(Si2) = 1 or 0, for
i = x, y, z.
Return to The Kochen-Specker Theorem
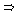
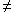 0 in state
|
0 in state
|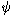 >. From this
assumption and KS2 (b) (Product Rule):
>. From this
assumption and KS2 (b) (Product Rule):