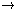Stanford Encyclopedia of Philosophy
Supplement to The Kochen-Specker Theorem
Citation Information

Derivation of Sum Rule and Product Rule from FUNC

FUNC: Let A be a self-adjoint operator associated with observable A, let f: RR be an arbitrary function, such that f(A) is self-adjoint operator, and let | f > be an arbitrary state; then f(A) is associated uniquely with an observable f(A) such that:

v(f(A)) = f(v(A))

Sum Rule: If A and B are commuting self-adjoint operators corresponding to observables A and B, respectively, then A + B is the unique observable corresponding to the self-adjoint operator A + B and

v(A + B) = v(A) + v(B)

Product Rule: If A and B are commuting self-adjoint operators corresponding to observables A and B, respectively, then if A B is the unique observable corresponding to the self-adjoint operator A B and

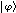
v(AB) = v(A) v(B)

So, for two commuting operators A, B:

Since A = f(C) and B = g(C), there is a function h = f+g, such that A + B = h(C).

v(A + B)	=	h(v(C))		(by FUNC)
	=	f(v(C)) + g(v(C))
	=	v(f(C)) + v(g(C))		(by FUNC)
	=	v(A) + v(B)		(Sum Rule)

Since A = f(C) and B = g(C), there is a function k = fg, such that AB = k(C).

v(A B)	=	k(v(C))		(by FUNC)
	=	f(v(C)) g(v(C))
	=	v(f(C)) v(g(C))		(by FUNC)
	=	v(A) v(B)		(Product Rule)

Return to The Kochen-Specker Theorem

Supplement to The Kochen-Specker Theorem
Stanford Encyclopedia of Philosophy