Notes
1. Im Jahre 1919 wurde
mir das Wort Selbstbestimmung, das in aller Leute Munde war,
Anlaß eines Versuches, mir einen klaren Begriff zu dem Wort zu
bilden. Natürlich stieß ich dabei alsbald auf die
Schwierigkeiten und Dunkelheiten des Sollensbegriffes: das Problem
wandelte sich. Grundbegriff aller Ethik, kann der Begriff des Sollens
ein brauchbares Fundament ihres Aufbaus nur geben, wenn er in einem
System von Axiomen festgelegt ist. Ein solches Axiomensystem
führe ich hier vor (Mally 1926, Preface, p. I).
2. Menger (1939, p. 57)
and Føllesdal and Hilpinen (1981, pp. 2-3) made the same
decision.
3. Menger (1939, p. 58)
said that Mally derived "fifty" theorems, while Føllesdal and
Hilpinen (1981, p. 3) said that Mally derived "about fifty"
theorems. They probably included some of Mally's unnumbered theorems,
which Mally mentioned only in passing. Our list consists of Mally's
thirty-six explicitly numbered theorems.
4. Diese letzten
Sätze, die Seinsollen und Tatsächlichsein zu identifizieren
scheinen, sind unter unseren "befremdlichen Folgerungen" wohl die
befremdlichsten (Mally 1926, p. 25).
5. The formula on this line
is a theorem of the classical propositional calculus because A
 (B
(B
 B) and A
B) and A
 (B
(B
 A)
are theorems of this calculus.
A)
are theorems of this calculus.
6. The formula on this
line is a theorem of the classical propositional calculus because
 ((U ((U  !A) & (A
!A) & (A

 )) )) |
 |
 ((U ((U  !A) & (U
!A) & (U

 A)) A)) |
|
 |
 (U (U
 (!A & (!A &
 A)) A)) |
|
 |
U &  (!A & (!A &
 A) A) |
|
 |
!A  A A |
7. On S3, see Hacking
1963. The proof that A
 !A is a theorem of S3 enriched with ! and supplemented with
I
!A is a theorem of S3 enriched with ! and supplemented with
I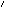 and
III
and
III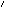 is straightforward and left to the reader.
is straightforward and left to the reader.
8. We only prove that I* is
a theorem of RD. The other five cases (II* and III* are
theorems of RD and I-III follow from I*-III*) are left to the
reader.
| 1. |
(!A  !A) &
(A !A) &
(A  ((A ((A
 B) B)
 B)) B)) |
[ R ] |
| 2. |
!A  !((A !((A
 B) B)
 B) B) |
[ 1, Ax. I, Def. f ] |
| 3. |
!A  ((A ((A
 B) B)
 !B) !B) |
[ 2, Ax. III(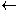 ), Def. f ] ), Def. f ] |
| 4. |
(A
 B) B)
 (!A (!A
 !B) !B) |
[ 3, Permutation ] |
9. Most cases are obvious
but some hints for (16)-(18) and (30) may be helpful. (16) is a
consequence of I* and IV. (17) follows from (16) and (18). (18) may
be proven as follows:
| 1. |
!(!A  A) &
!(!!A A) &
!(!!A  !A) !A) |
[ III* (twice), Adjunction ] |
| 2. |
!((!A  A) &
(!!A A) &
(!!A  !A)) !A)) |
[ 1, II* ] |
| 3. |
((!A
 A) & (!!A A) & (!!A
 !A)) !A))
 (!!A (!!A
 A) A) |
[ R ] |
| 4. |
!((!A  A) & (!!A A) & (!!A
 !A)) !A))
 !(!!A !(!!A
 A) A) |
[ 3, I* ] |
| 5. |
!(!!A  A) A) |
[ 2, 4 ] |
| 6. |
!!A  !A !A |
[ 5, Ax. III(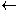 ), Def. f ] ), Def. f ] |
(30) is proven as follows: we have

 (V
(V

 ) by Ax. t, whence
) by Ax. t, whence

 (U
(U

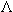 ) by Contraposition and Double Negation, whence
) by Contraposition and Double Negation, whence

 !
!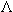 by (16).
by (16).
10. In order to prove this
claim, we first have to remove an obstacle: (2), (5), (15) and (27)
do not belong to the language of RD because they contain
propositional quantifiers. If such quantifiers were added in the
usual way (Anderson, Belnap & Dunn 1992, sec. 32), then we
could easily prove that (2), (5), (15) and (27) are deductively
equivalent with
(2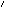 ),
(5
),
(5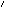 ),
(15
),
(15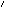 ) and
(27
) and
(27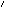 ), respectively:
), respectively:
(2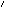 ) ) |
(A f
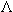 ) )
 (A f B) (A f B) |
(5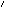 ) ) |
(!A
 (B f A)) & ((V f A) (B f A)) & ((V f A)
 !A) !A) |
(15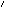 ) ) |
A f U |
(27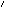 ) ) |
 f A f A |
To avoid needless complications, we will not equip RD with
quantifiers, but confine our attention to the unquantified versions
of (2), (5), (15) and (27). We may now proceed with the actual
proof. We use the following matrices:
|
|
|
|
|
|
| 5 |
5 |
5 |
5 |
5 |
5 |
| 0 |
1 |
2 |
3 |
4 |
5 |
| 0 |
0 |
1 |
1 |
3 |
5 |
| 0 |
0 |
0 |
1 |
2 |
5 |
| 0 |
0 |
0 |
0 |
1 |
5 |
| 0 |
0 |
0 |
0 |
0 |
5 |
|
|
|
|
|
|
|
|
| 0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
1 |
0 |
1 |
| 0 |
0 |
2 |
2 |
2 |
2 |
| 0 |
1 |
2 |
3 |
2 |
3 |
| 0 |
0 |
2 |
2 |
4 |
4 |
| 0 |
1 |
2 |
3 |
4 |
5 |
|
|
Each theorem M of RD has the following property: v(M)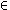 {1, 3, 5} for every assignment v of values
to the variables in M such that
{1, 3, 5} for every assignment v of values
to the variables in M such that
- v(A)
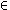 {0, 1, 2, 3, 4, 5},
{0, 1, 2, 3, 4, 5},
- v(V) = 1,
- v(U) = 2,
- v(
 A), v(A
A), v(A
 B)
and v(A & B) are as indicated in the tables,
B)
and v(A & B) are as indicated in the tables,
- v(A
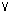 B) =
v(
B) =
v( (
( A &
A &
 B)), and
B)), and
- v(!A) = v(U
 A).
A).
(1), (2), (5), (7), (12), (13), (15), (19)-(23), (24)-(29),
(31)-(35), A
 !A and !A
!A and !A
 A (unquantified versions) lack this property, so these formulas are
not theorems of RD. (These matrices were discovered by the
computer program MaGIC. See the section Other Internet
Resources for information on this program. The claims we have
made were verified by a simple
Perl-script
of our own making.)
A (unquantified versions) lack this property, so these formulas are
not theorems of RD. (These matrices were discovered by the
computer program MaGIC. See the section Other Internet
Resources for information on this program. The claims we have
made were verified by a simple
Perl-script
of our own making.)
11. Menger's theorem A
 !A is a theorem of both RD+(34) and RD+(35):
!A is a theorem of both RD+(34) and RD+(35):
| 1. |
A
 (V (V
 A) A) |
[ Ax. t ] |
| 2. |
A
 (U (U
 A) A) |
[ 1, either (34) or (35) ] |
| 3. |
A
 !A !A |
[ 2, (16) ] |
| 4. |
(A

 ) )
 ((U ((U
 !A) !A)
 (U (U
 ! ! )) )) |
[ I*, Prefixing ] |
| 5. |
(A

 ) )
 ( ( (U (U
 ! ! ) )

 (U (U
 !A)) !A)) |
[ 4, Contraposition ] |
| 6. |
 (U (U
 ! ! ) )
 ((A ((A

 ) )

 (U (U
 !A)) !A)) |
[ 5, Permutation ] |
| 7. |
(A

 ) )

 (U (U
 !A) !A) |
[ 6, Ax. V, Def. f ] |
| 8. |
!A
 A A |
[ 2, 7, R ] |
| 9. |
A
 !A !A |
[ 3, 8, Adjunction ] |
However, neither (34) nor (35) is derivable in RD supplemented
with A
 !A. To prove this, we use the following table from Anderson and
Belnap 1975, p. 148:
!A. To prove this, we use the following table from Anderson and
Belnap 1975, p. 148:
Each theorem M of RD+{A
 !A} has the following property: v(M)
!A} has the following property: v(M)
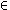 {1, 2}
for every assignment v of values to the variables in M such that
{1, 2}
for every assignment v of values to the variables in M such that
- v(A)
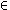 {0, 1, 2},
{0, 1, 2},
- v(V) = 1,
- v(U) = 2,
- v(
 A) and v(A
A) and v(A
 B) are as indicated in the table,
B) are as indicated in the table,
- v(A & B) = min{v(A), v(B)},
- v(A
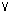 B) = max{v(A), v(B)}, and
B) = max{v(A), v(B)}, and
- v(!A) = v(A).
But v((34)) = v(U
 V) = 0 and v((35)) =
v(
V) = 0 and v((35)) =
v(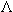

 ) = 0,
so (34) and (35) are not theorems of RD+{A
) = 0,
so (34) and (35) are not theorems of RD+{A
 !A}.
!A}.
12. See Lokhorst 1999,
pp. 277-278.
13. One may use the
three-valued matrices of note 11 to prove this.
14. Anderson 1967,
p. 348. However, Menger (1939, p. 59) had already defined
"I command p" as "unless p, something unpleasant will happen," or in
symbols: Cp
 (
( p
p
 A),
where Cp stands for "I command p" and A denotes the statement that
the unpleasant thing will happen.
A),
where Cp stands for "I command p" and A denotes the statement that
the unpleasant thing will happen.
15. One may use the
six-valued matrices of note 10 to prove this.
16. Wer richtig will,
will nicht (auch nicht impliziterweise) das Negat des Gewollten;
richtiges Wollen ist widerspruchsfrei (Mally 1926,
p. 49). Mally regarded this as a paraphrase of Axiom V, but
this is not entirely correct. Morscher (1998, p. 106) has
suggested that ARD2 expresses Mally's intentions more adequately than
Axiom V does.
17. ARD1 is a theorem of
RD+ARD1(
 )
by virtue of theorem (16), i.e., ARD1(
)
by virtue of theorem (16), i.e., ARD1(
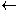 ).
This completes the proof. Notice that Axiom V is redundant
because we have !U by Ax. IV, whence
).
This completes the proof. Notice that Axiom V is redundant
because we have !U by Ax. IV, whence
 !
! by ARD2, whence
by ARD2, whence
 (U
(U

 ) by ARD1, whence
) by ARD1, whence
 (U
(U
 (U
(U

 )) by R, whence
)) by R, whence
 (U
(U
 !
! )
by ARD1, whence Axiom V by Def. f.
)
by ARD1, whence Axiom V by Def. f.
18. Morscher (1998) has
made a somewhat similar proposal, but the details are different. The
present approach was inspired by a number of suggestions made by
Lou Goble.
Notes to Mally's Deontic Logic
Stanford Encyclopedia of Philosophy
 (B
(B
 B) and A
B) and A
 (B
(B
 A)
are theorems of this calculus.
A)
are theorems of this calculus. (B
(B
 B) and A
B) and A
 (B
(B
 A)
are theorems of this calculus.
A)
are theorems of this calculus.((U
!A) & (A

))
((U
!A) & (U

A))
(U
(!A &
A))
(!A &
A)
A
 !A is a theorem of S3 enriched with ! and supplemented with
I
!A is a theorem of S3 enriched with ! and supplemented with
I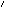 and
III
and
III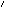 is straightforward and left to the reader.
is straightforward and left to the reader.!A) & (A
((A
B)
B))
!((A
B)
B)
((A
B)
!B)
), Def. f ]
B)
(!A
!B)
A) & !(!!A
!A)
A) & (!!A
!A))
A) & (!!A
!A))
(!!A
A)
A) & (!!A
!A))
!(!!A
A)
A)
!A
), Def. f ]

 (V
(V

 ) by Ax. t, whence
) by Ax. t, whence

 (U
(U

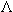 ) by Contraposition and Double Negation, whence
) by Contraposition and Double Negation, whence

 !
!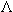 by (16).
by (16).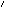 ),
(5
),
(5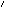 ),
(15
),
(15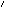 ) and
(27
) and
(27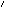 ), respectively:
), respectively:)
)
(A f B)
)
(B f A)) & ((V f A)
!A)
)
)
f A
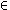 {1, 3, 5} for every assignment v of values
to the variables in M such that
{1, 3, 5} for every assignment v of values
to the variables in M such that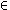 {0, 1, 2, 3, 4, 5},
{0, 1, 2, 3, 4, 5}, A), v(A
A), v(A
 B)
and v(A & B) are as indicated in the tables,
B)
and v(A & B) are as indicated in the tables,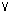 B) =
v(
B) =
v( (
( A &
A &
 B)), and
B)), and A).
A). !A and !A
!A and !A
 A (unquantified versions) lack this property, so these formulas are
not theorems of RD. (These matrices were discovered by the
computer program MaGIC. See the section Other Internet
Resources for information on this program. The claims we have
made were verified by a simple
Perl-script
of our own making.)
A (unquantified versions) lack this property, so these formulas are
not theorems of RD. (These matrices were discovered by the
computer program MaGIC. See the section Other Internet
Resources for information on this program. The claims we have
made were verified by a simple
Perl-script
of our own making.)
 !A is a theorem of both RD+(34) and RD+(35):
!A is a theorem of both RD+(34) and RD+(35):(V
A)
(U
A)
!A

)
((U
!A)
(U
!
))

)
(
(U
!
)

(U
!A))
(U
!
)
((A

)

(U
!A))

)

(U
!A)
A
!A
 !A. To prove this, we use the following table from Anderson and
Belnap 1975, p. 148:
!A. To prove this, we use the following table from Anderson and
Belnap 1975, p. 148: !A} has the following property: v(M)
!A} has the following property: v(M)
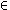 {1, 2}
for every assignment v of values to the variables in M such that
{1, 2}
for every assignment v of values to the variables in M such that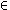 {0, 1, 2},
{0, 1, 2}, A) and v(A
A) and v(A
 B) are as indicated in the table,
B) are as indicated in the table,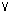 B) = max{v(A), v(B)}, and
B) = max{v(A), v(B)}, and V) = 0 and v((35)) =
v(
V) = 0 and v((35)) =
v(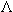

 ) = 0,
so (34) and (35) are not theorems of RD+{A
) = 0,
so (34) and (35) are not theorems of RD+{A
 !A}.
!A}.
 (
( p
p
 A),
where Cp stands for "I command p" and A denotes the statement that
the unpleasant thing will happen.
A),
where Cp stands for "I command p" and A denotes the statement that
the unpleasant thing will happen. )
by virtue of theorem (16), i.e., ARD1(
)
by virtue of theorem (16), i.e., ARD1(
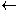 ).
This completes the proof. Notice that Axiom V is redundant
because we have !U by Ax. IV, whence
).
This completes the proof. Notice that Axiom V is redundant
because we have !U by Ax. IV, whence
 !
! by ARD2, whence
by ARD2, whence
 (U
(U

 ) by ARD1, whence
) by ARD1, whence
 (U
(U
 (U
(U

 )) by R, whence
)) by R, whence
 (U
(U
 !
! )
by ARD1, whence Axiom V by Def. f.
)
by ARD1, whence Axiom V by Def. f.