A Modern Formulation of Riemann's Theory

The multidimensional continua that Riemann was concerned with are essentially instances of what is now known as a real n-dimensional smooth manifold. For brevity, call them ‘n-manifolds’. (For example, a sphere, a Möbius strip and the surface of a Henry Moore sculpture may be regarded as 2-manifolds; the spacetimes models of current cosmology are 4-manifolds.) Conditions (a) – (c) provide a full characterization of n-manifolds.

(a) An n-manifold M is a set of points that can be pieced together from partially overlapping patches, such that every point of M lies in at least one patch.

(b) M is endowed with a neighborhood structure (a topology) such that, if U is a patch of M, there is a continuous one-one mapping f of U onto some region of Rⁿ, with continuous inverse f ⁻¹. (Rⁿ denotes here the collection of all real number n-tuples, with the standard topology generated by the open balls.) f is a coordinate system or chart of M; the k-th number in the n-tuple assigned by a chart f to a point P in f's patch is called the k-th coordinate of P by f; the k-th coordinate function of chart f is the real-valued function that assigns to each point of the patch its k-th coordinate by f.

(c) There is a collection A of charts of M, which contains at least one chart defined on each patch of M and is such that, if g and h belong to A, the composite mappings h g⁻¹ and g h⁻¹ — known as coordinate transformations — are differentiable to every order wherever they are well defined. (Denote the real number n-tuple <a₁, … , a_n> by a. The mapping h g⁻¹ is well defined at a if a is the valued assigned by g to some point P of M to which h also assigns a value. Suppose that the latter value h(P) = <b₁, … ,b_n> = b; then, b = h g⁻¹(a). Since h g⁻¹ maps a region of Rⁿ into Rⁿ, it makes sense to say that h g⁻¹ is differentiable.) Such a collection A is called an atlas.^[1]

It is the pair <M, A> that, strictly speaking, is an n-manifold, in the sense defined above. If <M₁,A₁> and <M₂,A₂> are an n-manifold and an m-manifold, respectively, it makes good sense to say that a mapping f of M₁ into M₂ is differentiable at a point P of M₁ if, for a chart h defined at P and a chart g defined at f(P), the composite mapping g 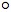 f 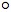 h⁻¹ is differentiable at h(P). (Condition (c) implies that the fulfillment of this requirement does not depend on the choice of h and g.) f is differentiable if it is differentiable at every point of M₁.

Let <M,A> be an n-manifold. To each point P of M one associates a vector space, which is known as the tangent space at P and is denoted by T_PM. The idea is based on the intuitive notion of a plane tangent to a surface at a given point. It can be constructed as follows. Let γ be a one-one differentiable mapping of a real open interval I into M. We can think of the successive values of γ as forming the path of a point that moves through M during a time interval represented by I. We call γ a curve in M (parametrized by u ∈ I). Put γ(t₀) = P for a fixed number t₀ in I. Consider the collection F(P) of all differentiable real-valued functions defined on some neighborhood of P. With the ordinary operations of function addition and multiplication by a constant, F(P) has the structure of a vector space. Each function f in F(P) varies smoothly with u, along the path of γ, in some neighborhood of P. Its rate of variation at P = γ(t₀) is properly expressed by the derivative d(f 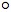γ)/du at u = t₀. 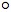As f ranges over F(P), the value of d(f γ)/du at u = t₀ is apt to vary in R. So we have here a mapping of F(P) into R, which we denote by γ·(u). It is in fact a linear function and therefore a vector in the dual space F*(P) of real-valued linear functions on F(P). Call it the tangent to γ at P. The tangents at P to all the curves whose paths go through P span an n-dimensional subspace of F*(P). This subspace is, by definition, the tangent space T_PM. The tangent spaces at all points of an n-manifold M can be bundled together in a natural way into a 2n-manifold TM. The projection mapping π of TM onto M assigns to each tangent vector v in T_PM the point π(v) at which v is tangent to M. The structure <TM,M,π> is the tangent bundle over M. A vector field on M is a section of TM, i.e., a differentiable mapping f of M into TM such that π f sends each point P of M to itself; such a mapping obviously assigns to P a vector in T_PM.

Any vector space V is automatically associated with other vector spaces, such as the dual space V* of linear functions on V, and the diverse spaces of multilinear functions on V, on V*, and on any possible combination of V and V*. This holds, of course, for each tangent space of an n-manifold M. The dual of T_PM is known as the cotangent space at P. There is a natural way of bundling together the cotangent spaces of M into a 2n-manifold, the cotangent bundle. Generally speaking, all the vector spaces of a definite type associated with the tangent and cotangent spaces of M can be naturally bundled together into a k-manifolds (for suitable integers k, depending on the nature of the bundled items). A section of any of these bundles is a tensor field on M (of rank r, if the bundled objects are r-linear functions).

A Riemannian metric g on the n-manifold <M,A> is a tensor field of rank 2 on M. Thus, g assigns to each P in M a bilinear function g_P on T_PM. For any P in M and any vectors v, w, in T_PM, g_P must meet these requirements:

1. g_P(v, w) = g_P(w, v)       (symmetry)
2. g_P(v, w) = 0 for all vectors w in T_PM if and only if v is the 0-vector       (non-degeneracy)
3. g_P(v, v) > 0 unless v is the 0-vector       (positive definiteness).

It is worth noting that the so-called Lorentzian metrics defined by relativity theory on its spacetime models meet requirements (i) and (ii), but not (iii), and are therefore usually said to be semi-Riemannian or pseudo-Riemannian.

The length λ(v) of a vector v in T_PM is defined by |λ(v)|² = g_P(v, v). Let γ be a curve in M. Let γ·(u) be the tangent to γ at the point γ(u). The length of γ's path from γ(a) to γ(b) is measured by the integral

∫

b a

λ(γ·(u))du

Thus, in Riemannian geometry, the length of the tangent vector γ·(u) bears witness to the advance of curve g as it passes through the point γ(u). The definition of the length of a curve leads at once to the notion of a geodesic (or straightest) curve, which is characterized by the fact that its length is extremal; in other words, a geodesic is either the greatest or the shortest among all the curves that trace out neighboring paths between the same two points.

In his study of curved surfaces, Gauss introduced a real-valued function, the Gaussian curvature, which measures a surface's local deviation from flatness in terms of the surface's intrinsic geometry. Riemann extended this concept of curvature to Riemannian n-manifolds. He observed that each geodesic through a point in such a manifold is fully determined by its tangent vector at that point. Consider a point P in a Riemannian n-manifold <M,A,g> and two linearly independent vectors v and w in T_PM. The geodesics determined by all linear combinations of v and w form a 2-manifold about P, with a definite Gaussian curvature K_P(v,w) at P. The real number K_P(v,w) measures the curvature of M at P in the “surface direction” (Riemann 1854, p. 145) fixed by v and w. In particular, if n = 3 and K_P(v,w) takes the same constant value k for every choice of the point P and of the vectors v and w, then the manifold <M,A,g> is a realization of Euclidian space if k = 0, of Lobachevskian space if k < 0, and of either spherical or elliptic space if k > 0. Riemann (1861) thought up a global mapping, depending on the metric g, that yields the appropriate values of K_P(v,w) on appropriate arguments P, v and w. Nowadays this object is conceived as a tensor field of rank 4, which assigns to each point P in a Riemannian n-manifold <M,A,g> a 4-linear function on the tangent space T_PM. It is therefore known as the Riemann tensor. Given the above definition of K_P(v,w) it is clear that, if n = 2, the Riemann tensor reduces to the Gaussian curvature function.

Return to Nineteenth Century Geometry