Supplement to Hermann Weyl
Weyl's metric-independent construction of the symmetric linear connection
Weyl characterizes the notion of a symmetric linear connection as follows:
Definition A.1 (Affine Connection) Let T(Mp) denote the tangent space of M at p ∈ M. A point p ∈ M is affinely connected with its immediate neighborhood, if and only if for every vector vp ∈ T(Mp), a vector at q
viq ∈ T(Mq) = vip + dvip (44)
is determined to which the vector vp ∈ T(Mp) gives rise under parallel displacement from p to the infinitesimally neighboring point q.
Of the notion of parallel displacement, Weyl requires that it satisfy the following condition.
Definition A.2 (Parallel Displacement) The transport of a vector vp ∈ T(Mp) to an infinitesimally neighboring point q ∈ M constitutes a parallel displacement if and only if there exists a coordinate system xi (called a geodesic coordinate system) for the neighborhood of p ∈ M, relative to which the transported vector vq possesses the same components as vp; that is,
viq −vip = dvip = 0. (45)
The requirement that there exist a geodesic coordinate system such that (45) is satisfied, characterizes the essential nature of parallel transport.
It is natural to require that for an arbitrary coordinate system the components dvip in (44) vanish whenever vip or dxip vanish. Hence, the simplest assumption that can be made about the components dvip is that they are linearly dependent on the two vectors vip and dxip. That is, dvip must be bilinear in vip and in dxip; that is,
dvip = −Γijk(x)vjpdxkp, (46)
where the n3 coefficients Γijk(x) are coordinate functions, that is functions of xi (i = 1, … , n), and the minus sign is introduced to agree with convention.
The vjp and dxkp in (46) are vectors, but dvip = viq − vip is not a vector since the vectors viq and vip lie in different tangent planes and cannot be subtracted. Hence the coefficients Γijk(x) do not constitute a tensor; they conform to a linear but non-homogeneous transformation law. The vector
viq = vip + dvip = vip − Γijkvjpdxkp
is called the parallel displaced vector.
Weyl (1918b, 1923b) proves the following theorem.
Theorem A.3 If for every point p in a neighborhood U of M, there exists a geodesic coordinate system x such that the change in the components of a vector under parallel transport to an infinitesimally near point q is given by
dvip = 0, (47)
then locally in any other coordinate system x,
dvip = −Γijk(x)vjpdxkp, (48)
where Γijk(x) = Γikj(x), and conversely.
The idea of parallel displacement leads immediately to the idea of the covariant derivative of a vector field. Consider a vector field vi(x) evaluated at two nearby points p and q with arbitrary coordinates xi and xi + δxi respectively. A first-order Taylor expansion yields
uiq = vip(x + δx) = vip(x) + δxjp.
∂vi ∂xj (49)
If we set
δxjp = δvip(x),
∂vi ∂xj (50)
then
δvip(x) = vip(x + δx) − vip(x), (51)
and
uiq = vip + δvip. (52)
The array of derivatives
∂vi ∂xj
do not constitute a tensorial entity, because the derivatives are formed by the inadmissible procedure of subtracting the vector vip(x) at p from the vector uiq = vip(x + δx) at q. Their difference δvip(x) is not a vector since the vectors lie in the different tangent spaces T(Mp) and T(Mq), respectively. Since δxip is a vector whereas δvip is not, the array of derivatives
∂vi ∂xj
in (50) cannot therefore be a tensorial entity. To form a derivative that is tensorial, that is covariant or invariant, we must subtract from the vector uiq = vip + δvip not the vector vip, but another vector at q which “represents” the original vector vip as “unchanged” as we proceed from p to q. Such a representative vector at q may be obtained by parallel transport of the vector vip to the nearby point q, and will be denoted, given an arbitrary coordinate system x, by
viq = vip + dvip. (53)
Since dvip is the difference between vip and viq, dvip is also not a vector for the for the reasons given above; however, the difference
uq − vq = vip + δvip − [vip + dvip] = δvip − dvip (54)
is a vector and is therefore a tensorial entity.
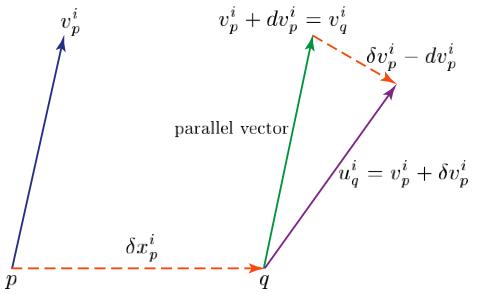
Figure 16: Covariant differentiation
The covariant derivative can now be defined by the limiting process
∇kvip = limδxkp →0
(vip + δvip − vip − dvip) δxkp = limδxkp →0
δvip − dvip δxkp = + Γijkvjp.
∂vip ∂xk (55)
In general, one writes the covariant derivative of a vector field vi simply as
∇kvi = ∂kvi + Γijkvj. (56)
Weyl (1918b, §3.I.B) also provided a more synthetic argument to establish the symmetry of the affine connection. He considers two infinitesimal vectors PP1 and PP2 at a point P. The vector PP1 under parallel transport along PP2 goes into P2P21. Similarly, the vector PP2 under parallel transport along PP1 goes into P1P12. These relationships are illustrated in figure 17
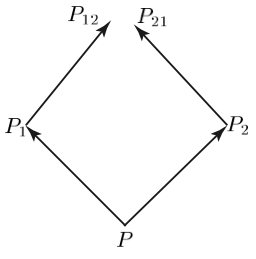
Figure 17: Symmetry of Parallel Transport
The condition imposed on parallel transport is that the four vectors PP1, P1P12, PP2 and P2P21 form a closed parallelogram; that is, the points P12 and P21 coincide. It follows that
PP1 + P1P12 = PP2 + P2P21. (57)
Denote the coordinates of PP1 and PP2 by dxi and δxi, respectively. The coordinates of P2P21 and P1P12 are respectively denoted by dxi + δdxi and δxi + dδxi. Substitution into (57) yields
dxi + δxi + dδxi = δxi + dxi + δdxi, (58)
or
dδxi = δdxi. (59)
From the assumption that the vectors transform linearly, one has
δdxi = −δγirdxr and dδxi = −dγirδxr. (60)
From the assumption that the infinitesimal transformation coefficients δγir and dγir are of the same order as the corresponding differentials δxi and dxi, one obtains
δγir = Γirsδxs and dγir = Γirsdxs. (61)
Substitution of (60) and (61) into (59) yields
Γijk = Γikj. (62)

