Supplement to Common Knowledge
Proof of Lemma 2.15
Lemma 2.15.ω′ ∈
 (ω)
iff ω′ is reachable from
ω.
(ω)
iff ω′ is reachable from
ω.
Proof.
Pick an arbitrary world ω ∈ Ω, and let
(ω) =
∞
∪
n=1
∪
i1,i2,…,in∈Nin (… (
i2 (
i1(ω)))
that is,
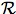 (ω)
is the
set of all worlds that are reachable from ω. Clearly, for each i
∈ N,
(ω)
is the
set of all worlds that are reachable from ω. Clearly, for each i
∈ N,
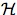 i(ω) ⊆
i(ω) ⊆
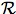 (ω),
which shows that
(ω),
which shows that
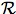 is a coarsening of the partitions
is a coarsening of the partitions
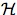 i,
i
∈ N.
Hence
i,
i
∈ N.
Hence
 (ω) ⊆
(ω) ⊆
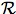 (ω),
as
(ω),
as
 is the finest common coarsening of the
is the finest common coarsening of the
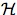 i's.
i's.
We need to show that
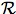 (ω)
⊆
(ω)
⊆
 (ω)
to complete the proof. To do this, it
suffices to show that for any sequence i1,
i2,
… , in ∈ N
(ω)
to complete the proof. To do this, it
suffices to show that for any sequence i1,
i2,
… , in ∈ N
(1) in (… (
i2 (
i1(ω)))
We will prove (1) by induction on n. By definition,
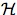 i(ω)
⊆
i(ω)
⊆
 (ω)
for each i ∈ N,
proving (1) for n = 1. Suppose now that (1) obtains for
n = k, and for
a given i ∈ N, let ω* ∈
(ω)
for each i ∈ N,
proving (1) for n = 1. Suppose now that (1) obtains for
n = k, and for
a given i ∈ N, let ω* ∈
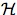 i(A) where A =
i(A) where A =
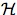 ik (…
(
ik (…
(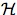 i2
(
i2
(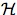 i1(ω))).
By induction hypothesis, A ⊆
i1(ω))).
By induction hypothesis, A ⊆
 (ω).
Since
(ω).
Since
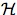 i(A)
states that i1 thinks
that i2 thinks that …
ik thinks that i
thinks that ω* is possible, A and
i(A)
states that i1 thinks
that i2 thinks that …
ik thinks that i
thinks that ω* is possible, A and
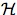 i(ω*)
must overlap, that is,
i(ω*)
must overlap, that is,
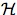 i(ω*)
∩ A ≠ Ø. If ω*
i(ω*)
∩ A ≠ Ø. If ω*
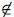
 (ω),
then
(ω),
then
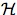 i(ω*)
i(ω*)
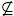
 (ω),
which implies that
(ω),
which implies that
 is not a common coarsening of
the
is not a common coarsening of
the
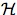 i's, a
contradiction. Hence ω* ∈
i's, a
contradiction. Hence ω* ∈
 (ω),
and since i was chosen arbitrarily
from N, this shows that (1) obtains for n = k + 1.
(ω),
and since i was chosen arbitrarily
from N, this shows that (1) obtains for n = k + 1.

Peter Vanderschraaf <peterv@cyrus.andrew.cmu.edu>
Giacomo Sillari <gsillari@andrew.cmu.edu>

