Proof of Proposition 3.1
Proposition 3.1.
Let Ω be a finite set of states of the world. Suppose that
- Agents i and j have a common prior probability distribution
μ(·) over the events of Ω such that μ(ω) >
0 for each ω ∈ Ω, and
- It is common knowledge at ω that i's posterior
probability of event E is qi(E) and that
j's posterior probability of E is qj(E).
Then
qi(E) =
qj(E).
Proof.
Let
 be the meet of all the
agents' partitions, and let
be the meet of all the
agents' partitions, and let
 (
ω) be the element of
(
ω) be the element of
 containing ω. Since
containing ω. Since
 (
ω) consists of cells common to every
agents information partition, we can write
(
ω) consists of cells common to every
agents information partition, we can write
 (ω) = (ω) = |
∪
k |
Hik, |
where each Hik ∈
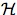 i. Since i's posterior probability of
event E is common knowledge, it is constant on
i. Since i's posterior probability of
event E is common knowledge, it is constant on
 (ω),
and so
(ω),
and so
| qi(E) = μ(E |
Hik) for all k |
Hence,
| μ( E ∩ Hik) = qi(E)
μ(Hik) |
and so
μ(E ∩
 (ω)) (ω)) |
|
= |
|
= |
|
|
= |
|
= |
|
|
= |
|
= |
|
|
= |
qi(E) μ( (ω)) (ω)) |
Applying the same argument to j, we have
μ(E ∩
 (ω))
= qj(E)
μ( (ω))
= qj(E)
μ( (ω)) (ω)) |
so we must have qi(E) = qj(E).

Return to Common Knowledge
 be the meet of all the
agents' partitions, and let
be the meet of all the
agents' partitions, and let
 (
ω) be the element of
(
ω) be the element of
 containing ω. Since
containing ω. Since
 (
ω) consists of cells common to every
agents information partition, we can write
(
ω) consists of cells common to every
agents information partition, we can write(ω) =
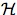 i. Since i's posterior probability of
event E is common knowledge, it is constant on
i. Since i's posterior probability of
event E is common knowledge, it is constant on
 (ω),
and so
(ω),
and so(ω))
(ω))
(ω)) = qj(E) μ(
(ω))


