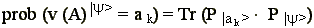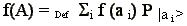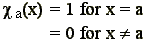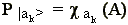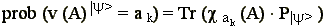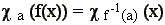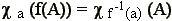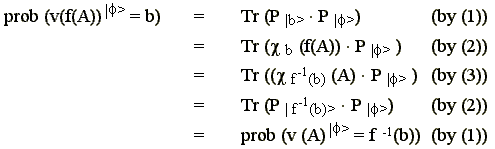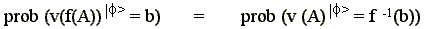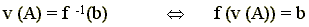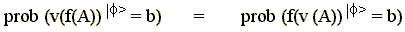Derivation of STAT FUNC
The result is proved for a pure state and a non-degenerate discrete
observable A with eigenvalues a
i.
We first rewrite the statistical algorithm for projection
operators:
| (1) |
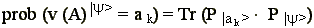 |
For an arbitrary function f:
R
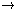 R
R (where
R is the set of real
numbers) we define the function of an observable A as:
Moreover, we introduce the characteristic function
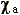
of a number a as:
As a result, we can rewrite a project operator
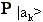
as:
| (2) |
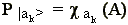 |
and thus the statistical algorithm as:
We also use a simple mathematical property of characteristic
functions:
whence we can also write:
| (3) |
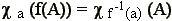 |
Then:
Hence:
Now since
which is STAT FUNC.
Return to The Kochen-Specker Theorem
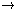 R (where R is the set of real
numbers) we define the function of an observable A as:
R (where R is the set of real
numbers) we define the function of an observable A as:
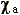 of a number a as:
of a number a as:
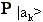 as:
as: