Supplement to Deontic Logic
The Logical Necessity of Obligations Problem[1]
Consider
(1) Nothing is obligatory.
A natural representation of this in the language of SDL would be:
(1′) ~OBq, for all q.
We noted above that OB-NEC entails
OB-N:
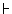 OB
OB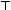 ;
but given (1′), we get
~OB
;
but given (1′), we get
~OB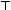 ,
and thus a contradiction. SDL seems to imply that it is a truth of
logic that something is always obligatory. But it seems that what (1)
expresses, an absence of obligations, is possible. For example,
consider a time when no rational agents existed in the universe. Why
should we think that any obligations existed then?
,
and thus a contradiction. SDL seems to imply that it is a truth of
logic that something is always obligatory. But it seems that what (1)
expresses, an absence of obligations, is possible. For example,
consider a time when no rational agents existed in the universe. Why
should we think that any obligations existed then?
von Wright 1951 notes that since the denial of
~OB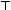 is provably
equivalent to PE⊥ (given the traditional definitional
scheme and OB-RE), and since both
OB
is provably
equivalent to PE⊥ (given the traditional definitional
scheme and OB-RE), and since both
OB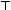 and PE⊥ are odd, we should opt
for a “principle of contingency,” which says that
OB
and PE⊥ are odd, we should opt
for a “principle of contingency,” which says that
OB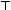 and ~PE⊥ are both logically contingent. von Wright
1963 argues that
OB
and ~PE⊥ are both logically contingent. von Wright
1963 argues that
OB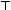 (and PE
(and PE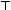 )
do not express real prescriptions (pp.152-4). Føllesdal and
Hilpinen 1971 suggests that excluding OB-N only
excludes “empty normative systems” (i.e.,
normative systems with no obligations), and perhaps not even that,
since no one can fail to fulfill
OB
)
do not express real prescriptions (pp.152-4). Føllesdal and
Hilpinen 1971 suggests that excluding OB-N only
excludes “empty normative systems” (i.e.,
normative systems with no obligations), and perhaps not even that,
since no one can fail to fulfill
OB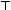 anyway, so why worry (p.13; cf. Prior 1958) However, since it is
dubious that anyone can bring it about that
anyway, so why worry (p.13; cf. Prior 1958) However, since it is
dubious that anyone can bring it about that
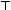 , it would seem to be equally
dubious that anyone can “fulfill”
OB
, it would seem to be equally
dubious that anyone can “fulfill”
OB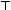 ,
and thus matters are not so simple. al-Hibri 1978 discusses various
early takes on this problem, rejects OB-N, and later
develops a deontic logic without it. Jones and Porn 1985 explicitly
rejects OB-N for “ought” in the system
developed there, where the concern is with what people ought to do. If
we are reading OB as simply “it ought to be the
case that”, it is not clear that there is anything
counterintuitive about
OB
,
and thus matters are not so simple. al-Hibri 1978 discusses various
early takes on this problem, rejects OB-N, and later
develops a deontic logic without it. Jones and Porn 1985 explicitly
rejects OB-N for “ought” in the system
developed there, where the concern is with what people ought to do. If
we are reading OB as simply “it ought to be the
case that”, it is not clear that there is anything
counterintuitive about
OB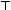 (now read as, essentially, “it ought to be that contradictions
are false”), but there is also no longer any obvious connection
to what is obligatory or permissible for that reading, or to what
people ought to do.
(now read as, essentially, “it ought to be that contradictions
are false”), but there is also no longer any obvious connection
to what is obligatory or permissible for that reading, or to what
people ought to do.
Return to Deontic Logic.

