Infinitary Logic
Traditionally, expressions in formal systems have been regarded as signifying finite inscriptions which are—at least in principle—capable of actually being written out in primitive notation. However, the fact that (first-order) formulas may be identified with natural numbers (via "Gödel numbering") and hence with finite sets makes it no longer necessary to regard formulas as inscriptions, and suggests the possibility of fashioning "languages" some of whose formulas would be naturally identified as infinite sets. A "language" of this kind is called an infinitary language: in this article I discuss those infinitary languages which can be obtained in a straightforward manner from first-order languages by allowing conjunctions, disjunctions and, possibly, quantifier sequences, to be of infinite length. In the course of the discussion it will be seen that, while the expressive power of such languages far exceeds that of their finitary (first-order) counterparts, very few of them possess the "attractive" features (e.g., compactness and completeness) of the latter. Accordingly, the infinitary languages that do in fact possess these features merit special attention.
In §1 the basic syntax and semantics of infinitary languages are laid down; their expressive power is then displayed by means of examples. §2 is devoted to those infinitary languages which permit only finite quantifier sequences: these languages turn out to be relatively well-behaved. §3 is devoted to a discussion of the compactness problem for infinitary languages and its connection with purely set-theoretical questions concerning "large" cardinal numbers. In §4 an argument is sketched which shows that most "infinite quantifier" languages have a second-order nature and are, ipso facto, highly incomplete. §5 provides a brief account of a certain special class of sublanguages of infinitary languages for which a satisfactory generalization of the compactness theorem can be proved. (This section links to a Supplement on the definition of admissible sets.) Historical and bibliographical remarks are provided in §6.
- 1. Definition and Basic Properties of Infinitary Languages
- 2. Finite-Quantifier Languages
- 3. The Compactness Property
- 4. Incompleteness of Infinite-Quantifier Languages
- 5. Sublanguages of
 (ω1,ω) and the Barwise Compactness Theorem
(ω1,ω) and the Barwise Compactness Theorem
- 6. Historical and Bibliographical Remarks
- Bibliography
- Other Internet Resources
- Related Entries
1. Definition and Basic Properties of Infinitary Languages
Given a pair κ, λ of infinite cardinals such that λ ≤ κ, we define a class of infinitary languages in each of which we may form conjunctions and disjunctions of sets of formulas of cardinality < κ, and quantifications over sequences of variables of length < λ.
Let
 — the (finitary)
base language — be an arbitrary but fixed first-order
language with any number of extralogical symbols. The infinitary
language
— the (finitary)
base language — be an arbitrary but fixed first-order
language with any number of extralogical symbols. The infinitary
language
 (κ,λ)
has
the following basic symbols:
(κ,λ)
has
the following basic symbols:
- All symbols of

- A set Var of individual variables, where the cardinality of Var (written: |Var|) is κ
- A logical operator
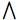 (infinitary conjunction)
(infinitary conjunction)
The class of preformulas of
 (κ,λ)
is defined recursively as
follows:
(κ,λ)
is defined recursively as
follows:
- Each formula of
 is a
preformula;
is a
preformula; - if φ and ψ are preformulas, so are
φ
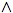 ψ and ¬φ;
ψ and ¬φ; - if Φ is a set of preformulas such that |Φ| < κ,
then
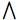 Φ
is a
preformula;
Φ
is a
preformula; - if φ is a preformula and X ⊆ Var is such that |X| < λ, then ∃Xφ is a preformula;
- all preformulas are defined by the above clauses.
If Φ is a set of preformulas indexed by a set I, say
Φ = {φi : i ∈ I},
then we agree to write
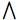 Φ
for:
Φ
for:
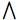
i∈Iφ
or, if I is the set of natural numbers, we write
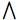 Φ
for:
Φ
for:
φ0φ1
…
If X is a set of individual variables indexed by an ordinal α, say X = {xξ : ξ < α}, we agree to write (∃xξ)ξ<αφ for ∃Xφ.
The logical operators
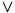 ,
→,
↔ are defined in the customary manner. We also introduce the
operators
,
→,
↔ are defined in the customary manner. We also introduce the
operators
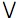 (infinitary
disjunction) and ∀ (universal quantification)
by
(infinitary
disjunction) and ∀ (universal quantification)
by
and employ similar conventions as forΦ =df ¬
{ ¬φ : φ ∈ Φ}
∀Xφ =df ¬∃X¬φ,
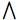 ,
∃ .
,
∃ .
Thus
 (κ,λ)
is
the infinitary language obtained from
(κ,λ)
is
the infinitary language obtained from
 by permitting conjunctions and disjunctions of length
< κ and quantifications[1]
of length <
λ. Languages
by permitting conjunctions and disjunctions of length
< κ and quantifications[1]
of length <
λ. Languages
 (κ,ω)
are called finite-quantifier
languages, the rest infinite-quantifier languages. Observe
that
(κ,ω)
are called finite-quantifier
languages, the rest infinite-quantifier languages. Observe
that
 (ω,ω)
is
just
(ω,ω)
is
just
 itself.
itself.
Notice the following anomaly which can arise in an
infinitary language but not in a finitary one. In the language
 (ω1,ω), which
allows countably infinite conjunctions but only finite quantifications,
there are preformulas with so many free variables that they cannot be
"closed" into sentences of
(ω1,ω), which
allows countably infinite conjunctions but only finite quantifications,
there are preformulas with so many free variables that they cannot be
"closed" into sentences of
 (ω1,ω) by prefixing quantifiers.
Such is the case, for example, for the
(ω1,ω) by prefixing quantifiers.
Such is the case, for example, for the
 (ω1,ω)-preformula
(ω1,ω)-preformula
x0 < x1wherex1 < x2
…
xn < xn+1 …,
 contains the binary
relation symbol <. For this reason we make the following
contains the binary
relation symbol <. For this reason we make the following
Definition. A formula ofIn this connection, observe that, in general, nothing would be gained by considering "languages"(κ,λ) is a preformula which contains < λ free variables. The set of all formulas of
(κ,λ) will be denoted by Form(
(κ,λ)) or simply Form(κ,λ) and the set of all sentences by Sent(
(κ,λ)) or simply Sent(κ,λ).
 (κ,λ)
with λ > κ. For
example, in the "language"
(κ,λ)
with λ > κ. For
example, in the "language"
 (ω,ω1), formulas will have only
finitely many free variables, while there will be a host of "useless"
quantifiers able to bind infinitely many free
variables.[2]
(ω,ω1), formulas will have only
finitely many free variables, while there will be a host of "useless"
quantifiers able to bind infinitely many free
variables.[2]
Having defined the syntax of
 (κ,λ),
we next sketch its
semantics. Since the extralogical symbols of
(κ,λ),
we next sketch its
semantics. Since the extralogical symbols of
 (κ,λ)
are just those
of
(κ,λ)
are just those
of
 , and it is these symbols which
determine the form of the structures in which a given first-order
language is to be interpreted, it is natural to define an
, and it is these symbols which
determine the form of the structures in which a given first-order
language is to be interpreted, it is natural to define an
 (κ,λ)-structure
to be
simply an
(κ,λ)-structure
to be
simply an
 -structure.
The notion
of a formula of
-structure.
The notion
of a formula of
 (κ,λ)
being satisfied in an
(κ,λ)
being satisfied in an
 -structure
A (by a sequence of elements from the domain
of A) is defined in the same inductive manner
as for formulas of
-structure
A (by a sequence of elements from the domain
of A) is defined in the same inductive manner
as for formulas of
 except that
we must add two extra clauses corresponding to the clauses for
except that
we must add two extra clauses corresponding to the clauses for
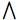 Φ
and ∃Xφ in the
definition of preformula. In these two cases we naturally define:
Φ
and ∃Xφ in the
definition of preformula. In these two cases we naturally define:
Φ is satisfied in A (by a given sequence) ⇔ for all φ ∈ Φ, φ is satisfied in A (by the sequence);
∃Xφ is satisfied in A ⇔ there is a sequence of elements from the domain of A in bijective correspondence with X which satisfies φ in A.
These informal definitions need to be tightened up in a rigorous
development, but their meaning should be clear to the reader. Now the
usual notions of truth, validity, satisfiability, and
model for formulas and sentences of
 (κ,λ)
become available. In particular, if
A is an
(κ,λ)
become available. In particular, if
A is an
 -structure
and σ ∈
Sent(κ,λ), we shall write
A
-structure
and σ ∈
Sent(κ,λ), we shall write
A
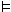 σ
for A is a model of σ, and
σ
for A is a model of σ, and
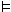 σ for σ is valid,
that is, for all A,
A
σ for σ is valid,
that is, for all A,
A
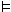 σ.
If Δ ⊆ Sent(κ,λ), we
shall write Δ
σ.
If Δ ⊆ Sent(κ,λ), we
shall write Δ
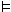 σ for
σ is a logical consequence of Δ, that is, each
model of Δ is a model of σ.
σ for
σ is a logical consequence of Δ, that is, each
model of Δ is a model of σ.
We now give some examples intended to display the expressive power
of the infinitary languages
 (κ,λ)
with κ ≥
ω1. In each case it is well-known that the notion in
question cannot be expressed in any first-order language.
(κ,λ)
with κ ≥
ω1. In each case it is well-known that the notion in
question cannot be expressed in any first-order language.
Characterization of the standard model of arithmetic
in
 (ω1,ω). Here the standard
model of arithmetic is the structure N =
(N, +, ·, s, 0), where N is the set
of natural numbers, +, ·, and 0 have their usual meanings, and
s is the successor operation. Let
(ω1,ω). Here the standard
model of arithmetic is the structure N =
(N, +, ·, s, 0), where N is the set
of natural numbers, +, ·, and 0 have their usual meanings, and
s is the successor operation. Let
 be the first-order language appropriate for
N. Then the class of
be the first-order language appropriate for
N. Then the class of
 -structures
isomorphic to N coincides
with the class of models of the conjunction of the following
-structures
isomorphic to N coincides
with the class of models of the conjunction of the following
 (ω1,ω)
sentences (where 0 is a name of 0):
(ω1,ω)
sentences (where 0 is a name of 0):
The terms snx are defined recursively by s0x = x; sn+1x = s(snx).
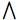
m∈ω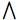
n∈ωsm0 + sn0 = sm+n0
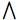
m∈ω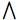
n∈ωsm0 · sn0 = sm·n0
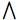
m∈ω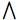
n∈ω−{m}sm0 ≠ sn0
∀x
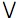
m∈ωx = sm0
Characterization of the class of all finite sets in
 (ω1,ω).
Here the base language has no extralogical symbols. The class of all
finite sets then coincides with the class of models of the
(ω1,ω).
Here the base language has no extralogical symbols. The class of all
finite sets then coincides with the class of models of the
 (ω1,ω)-sentence
(ω1,ω)-sentence
n∈ω ∃v0 … ∃vn∀x(x = v0
…
x = vn).
Truth definition in
 (ω1,ω) for a countable
base language
(ω1,ω) for a countable
base language
 .
Let
.
Let
 be a countable first-order
language (for example, the language of arithmetic or set theory) which
contains a name n for each natural number
n, and let σ0, σ1, …
be an enumeration of its sentences. Then the
be a countable first-order
language (for example, the language of arithmetic or set theory) which
contains a name n for each natural number
n, and let σ0, σ1, …
be an enumeration of its sentences. Then the
 (ω1,ω)-formula
(ω1,ω)-formula
Tr(x) =dfis a truth predicate forn∈ω (x = n
σn)
 inasmuch as the sentence
inasmuch as the sentence
Tr(n) ↔ σnis valid for each n.
Characterization of well-orderings in
 (ω1,ω1). The base
language
(ω1,ω1). The base
language
 here includes a binary
predicate symbol ≤. Let σ1 be the usual
here includes a binary
predicate symbol ≤. Let σ1 be the usual
 -sentence
characterizing linear
orderings. Then the class of
-sentence
characterizing linear
orderings. Then the class of
 -structures
in which the interpretation of ≤ is a
well-ordering coincides with the class of models of the
-structures
in which the interpretation of ≤ is a
well-ordering coincides with the class of models of the
 (ω1,ω1) sentence
σ = σ1
(ω1,ω1) sentence
σ = σ1
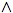 σ2, where
σ2, where
σ2 =df (∀vn)n∈ω ∃x [Notice that the sentence σ2 contains an infinite quantifier: it expresses the essentially second-order assertion that every countable subset has a least member. It can in fact be shown that the presence of this infinite quantifier is essential: the class of well-ordered structures cannot be characterized in any finite-quantifier language. This example indicates that infinite-quantifier languages such asn∈ω (x = vn)
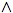
n∈ω (x≤ vn)].
 (ω1,ω1) behave rather
like second-order languages; we shall see that they share the latters'
defects (incompleteness) as well as some of their advantages (strong
expressive power).
(ω1,ω1) behave rather
like second-order languages; we shall see that they share the latters'
defects (incompleteness) as well as some of their advantages (strong
expressive power).
Many extensions of first-order languages can be translated
into infinitary languages. For example, consider the generalized
quantifier language
 (Q0) obtained from
(Q0) obtained from
 by adding a new quantifier symbol
Q0 and interpreting
Q0xφ(x) as there exist
infinitely many x such that φ(x). It is easily seen
that the sentence Q0xφ(x) has
the same models as the
by adding a new quantifier symbol
Q0 and interpreting
Q0xφ(x) as there exist
infinitely many x such that φ(x). It is easily seen
that the sentence Q0xφ(x) has
the same models as the
 (ω1,ω)-sentence
(ω1,ω)-sentence
¬n∈ω ∃v0…∃vn∀ x[φ(x) → (x = v0
…
x = vn)].
Thus
 (Q0)
is, in a natural sense, translatable into
(Q0)
is, in a natural sense, translatable into
 (ω1,ω). Another language
translatable into
(ω1,ω). Another language
translatable into
 (ω1,ω) in this sense is the
weak second-order language obtained by adding a countable set
of monadic predicate variables to
(ω1,ω) in this sense is the
weak second-order language obtained by adding a countable set
of monadic predicate variables to
 which are then interpreted as ranging over all
finite sets of individuals.
which are then interpreted as ranging over all
finite sets of individuals.
Languages with arbitrarily long conjunctions, disjunctions and
(possibly) quantifications may also be introduced. For a fixed infinite
cardinal λ, the language
 (∞,λ)
is defined by specifying its class
of formulas, Form(∞,λ), to be the union,
over all κ ≥ λ, of the sets
Form(κ,λ). Thus
(∞,λ)
is defined by specifying its class
of formulas, Form(∞,λ), to be the union,
over all κ ≥ λ, of the sets
Form(κ,λ). Thus
 (∞,λ)
allows arbitrarily long conjunctions
and disjunctions, in the sense that if Φ is an arbitrary subset of
Form(∞,λ), then both
(∞,λ)
allows arbitrarily long conjunctions
and disjunctions, in the sense that if Φ is an arbitrary subset of
Form(∞,λ), then both
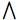 Φ
and
Φ
and
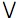 Φ
are members of
Form(∞,λ). But
Φ
are members of
Form(∞,λ). But
 (∞,λ)
admits only quantifications of
length < λ: all its formulas have < λ free
variables. The language
(∞,λ)
admits only quantifications of
length < λ: all its formulas have < λ free
variables. The language
 (∞,∞)
is defined in turn by specifying its
class of formulas, Form(∞,∞), to be the
union, over all infinite cardinals λ, of the classes
Form(∞,λ). So
(∞,∞)
is defined in turn by specifying its
class of formulas, Form(∞,∞), to be the
union, over all infinite cardinals λ, of the classes
Form(∞,λ). So
 (∞,∞)
allows arbitrarily long
quantifications in addition to arbitrarily long conjunctions and
disjunctions. Note that Form(∞,λ) and
Form(∞,∞) are proper classes in the sense
of Gödel-Bernays set theory. Satisfaction of formulas of
(∞,∞)
allows arbitrarily long
quantifications in addition to arbitrarily long conjunctions and
disjunctions. Note that Form(∞,λ) and
Form(∞,∞) are proper classes in the sense
of Gödel-Bernays set theory. Satisfaction of formulas of
 (∞,λ)
and
(∞,λ)
and
 (∞,∞)
in a structure may
be defined by an obvious extension of the corresponding notion for
(∞,∞)
in a structure may
be defined by an obvious extension of the corresponding notion for
 (κ,λ).
(κ,λ).
2. Finite-Quantifier Languages
We have remarked that infinite-quantifier languages such as (ω1,ω1) resemble
second-order languages inasmuch as they allow quantification over
infinite sets of individuals. The fact that this is not permitted in
finite-quantifier languages suggests that these may be in certain
respects closer to their first-order counterparts than might be evident
at first sight. We shall see that this is indeed the case, notably in
the case of
(ω1,ω1) resemble
second-order languages inasmuch as they allow quantification over
infinite sets of individuals. The fact that this is not permitted in
finite-quantifier languages suggests that these may be in certain
respects closer to their first-order counterparts than might be evident
at first sight. We shall see that this is indeed the case, notably in
the case of
 (ω1,ω).
(ω1,ω).
The language
 (ω1,ω) occupies a special place
among infinitary languages because—like first-order
languages—it admits an effective deductive apparatus. In
fact, let us add to the usual first-order axioms and rules of inference
the new axiom scheme
(ω1,ω) occupies a special place
among infinitary languages because—like first-order
languages—it admits an effective deductive apparatus. In
fact, let us add to the usual first-order axioms and rules of inference
the new axiom scheme
for any countable set Φ ⊆ Form(ω1,ω) and any φ ∈ Φ, together with the new rule of inferenceΦ → φ
and allow deductions to be of countable length. Writing
φ0, φ1, …, φn, …
n∈ω φn
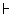 *
for deducibility in this sense, we
then have the
*
for deducibility in this sense, we
then have the
As an immediate corollary we infer that this deductive apparatus is adequate for deductions from countable sets of premises in(ω1,ω)-Completeness Theorem. For any σ ∈ Sent(ω1,ω),
σ ⇔
*σ
 (ω1,ω).
That is, with the obvious extension of notation, we have, for any
countable set Δ ⊆
Sent(ω1,ω)
(ω1,ω).
That is, with the obvious extension of notation, we have, for any
countable set Δ ⊆
Sent(ω1,ω)
(2.1) Δσ ⇔ Δ
*σ
This completeness theorem can be proved by modifying the usual Henkin completeness proof for first-order logic, or by employing Boolean-algebraic methods. Similar arguments, applied to suitable further augmentations of the axioms and rules of inference, yield analogous completeness theorems for many other finite-quantifier languages.
If just deductions of countable length are admitted, then no
deductive apparatus for
 (ω1,ω) can be set up which is
adequate for deductions from arbitrary sets of premises, that
is, for which (2.1) would hold for every set Δ ⊆
Sent(ω1,ω), regardless of
cardinality. This follows from the simple observation that there
is a first-order language
(ω1,ω) can be set up which is
adequate for deductions from arbitrary sets of premises, that
is, for which (2.1) would hold for every set Δ ⊆
Sent(ω1,ω), regardless of
cardinality. This follows from the simple observation that there
is a first-order language
 and
an uncountable set Γ of
and
an uncountable set Γ of
 (ω1,ω)-sentences such that
Γ has no model but every countable subset of Γ
does. To see this, let
(ω1,ω)-sentences such that
Γ has no model but every countable subset of Γ
does. To see this, let
 be
the language of arithmetic augmented by ω1 new
constant symbols {cξ : ξ
< ω1} and let Γ be the set of
be
the language of arithmetic augmented by ω1 new
constant symbols {cξ : ξ
< ω1} and let Γ be the set of
 (ω1,ω)-sentences {σ} ∪
{cξ ≠
cη : ξ ≠ η}, where
σ is the
(ω1,ω)-sentences {σ} ∪
{cξ ≠
cη : ξ ≠ η}, where
σ is the
 (ω1,ω)-sentence characterizing
the standard model of arithmetic. This example also shows that the
compactness theorem fails for
(ω1,ω)-sentence characterizing
the standard model of arithmetic. This example also shows that the
compactness theorem fails for
 (ω1,ω) and so also for any
(ω1,ω) and so also for any
 (κ,λ)
with κ ≥
ω1.
(κ,λ)
with κ ≥
ω1.
Another result which holds in the first-order case but fails
for
 (κ,ω) with κ
≥ ω1 (and also for
(κ,ω) with κ
≥ ω1 (and also for
 (ω1,ω1), although
this is more difficult to prove) is the prenex normal form
theorem. A sentence is prenex if all its quantifiers
appear at the front; we give an example of an
(ω1,ω1), although
this is more difficult to prove) is the prenex normal form
theorem. A sentence is prenex if all its quantifiers
appear at the front; we give an example of an
 (ω1,ω)-sentence which is not
equivalent to a conjunction of prenex sentences. Let
(ω1,ω)-sentence which is not
equivalent to a conjunction of prenex sentences. Let
 be the first-order language without
extralogical symbols and let σ be the
be the first-order language without
extralogical symbols and let σ be the
 (ω1,ω)-sentence which
characterizes the class of finite sets. Suppose that σ were
equivalent to a conjunction
(ω1,ω)-sentence which
characterizes the class of finite sets. Suppose that σ were
equivalent to a conjunction
of prenexi∈I σi
 (ω1,ω)-sentences
σi. Then each σi is
of the form
(ω1,ω)-sentences
σi. Then each σi is
of the form
Q1x1 … Qnxn φi(x1,…, xn),where each Qk is ∀ or ∃ and φi is a (possibly infinitary) conjunction or disjunction of formulas of the form xk = xl or xk ≠ xl. Since each σi is a sentence, there are only finitely many variables in each φi, and it is easy to see that each φi is then equivalent to a first-order formula. Accordingly each σi may be taken to be a first-order sentence. Since σ is assumed to be equivalent to the conjunction of the σi, it follows that σ and the set Δ = {σi : i ∈ I} have the same models. But obviously σ, and hence also Δ, have models of all finite cardinalities; the compactness theorem for sets of first-order sentences now implies that Δ, and hence also σ, has an infinite model, contradicting the definition of σ.
Turning to the Löwenheim-Skolem theorem, we find that
the downward version has adequate generalizations to
 (ω1,ω) (and,
indeed, to all infinitary languages). In fact, one can show in much the
same way as for sets of first-order sentences that if Δ ⊆
Sent(ω1,ω) has an infinite
model of cardinality ≥ |Δ|, it has a model of cardinality the
larger of
(ω1,ω) (and,
indeed, to all infinitary languages). In fact, one can show in much the
same way as for sets of first-order sentences that if Δ ⊆
Sent(ω1,ω) has an infinite
model of cardinality ≥ |Δ|, it has a model of cardinality the
larger of
 0, |Δ|.
In particular, any
0, |Δ|.
In particular, any
 (ω1,ω)-sentence with an infinite
model has a countable model.
(ω1,ω)-sentence with an infinite
model has a countable model.
On the other hand, the upward Löwenheim-Skolem theorem
in its usual form fails for all infinitary languages. For
example, the
 (ω1,ω)-sentence characterizing
the standard model of arithmetic has a model of cardinality
(ω1,ω)-sentence characterizing
the standard model of arithmetic has a model of cardinality
 0 but no models of any other
cardinality. However, all is not lost here, as we shall see.
0 but no models of any other
cardinality. However, all is not lost here, as we shall see.
We define the Hanf number h(L) of a language L to be the least cardinal κ such that, if an L-sentence has a model of cardinality κ, it has models of arbitrarily large cardinality. The existence of h(L) is readily established. For each L-sentence σ not possessing models of arbitrarily large cardinality let κ(σ) be the least cardinal κ such that σ does not have a model of cardinality κ. If λ is the supremum of all the κ(σ), then, if a sentence of L has a model of cardinality λ, it has models of arbitrarily large cardinality.
Define the cardinals μ(α) recursively by
μ(0) =Then it can be shown that0
μ(α+1) = 2μ(α)
μ(λ) = ∑α<λ μ(α), for limit λ.
h(similar results holding for other finite-quantifier languages. The values of the Hanf numbers of infinite-quantifier languages such as(ω1,ω)) = μ(ω1),
 (ω1,ω1) are sensitive
to the presence or otherwise of large cardinals, but must in any case
greatly exceed that of
(ω1,ω1) are sensitive
to the presence or otherwise of large cardinals, but must in any case
greatly exceed that of
 (ω1,ω).
(ω1,ω).
A result for
 which
generalizes to
which
generalizes to
 (ω1,ω) but to no other
infinitary language is the
(ω1,ω) but to no other
infinitary language is the
Craig Interpolation Theorem: If σ,τ ∈ Sent(ω1,ω) are such thatThe proof is a reasonably straightforward extension of the first-order case.σ → τ, then there is θ ∈ Sent(ω1,ω) such that
σ → θ and
θ → τ, and each extralogical symbol occurring in θ occurs in both σ and τ.
Finally, we mention one further result which generalizes nicely
to
 (ω1,ω)
but to no other infinitary language. It is well known that, if
A is any finite
(ω1,ω)
but to no other infinitary language. It is well known that, if
A is any finite
 -structure
with only finitely many relations, there is
an
-structure
with only finitely many relations, there is
an
 -sentence
σ
characterizing A up to isomorphism. For
-sentence
σ
characterizing A up to isomorphism. For
 (ω1,ω) we have
the following generalization known as
(ω1,ω) we have
the following generalization known as
Scott's Isomorphism Theorem. If A is a countableThe restriction to countable structures is essential because countability cannot in general be expressed by an-structure with only countably many relations, then there is an
(ω1,ω)-sentence whose class of countable models coincides with the class of
-structures isomorphic with A.
 (ω1,ω)-sentence.
(ω1,ω)-sentence.
The language
 (∞,ω)
may also be counted as a
finite-quantifier language. The concept of equivalence of structures
with respect to this language is of especial significance: we call two
(similar) structures A and
B (∞,ω)-equivalent,
written A ≡∞ω
B, if the same sentences of
(∞,ω)
may also be counted as a
finite-quantifier language. The concept of equivalence of structures
with respect to this language is of especial significance: we call two
(similar) structures A and
B (∞,ω)-equivalent,
written A ≡∞ω
B, if the same sentences of
 (∞,ω)
hold in both
A and B. This
relation can, first of all, be characterized in terms of the notion of
partial isomorphism. A partial isomorphism between
A and B is a
nonempty family P of maps such that:
(∞,ω)
hold in both
A and B. This
relation can, first of all, be characterized in terms of the notion of
partial isomorphism. A partial isomorphism between
A and B is a
nonempty family P of maps such that:
- For each p ∈ P, dom(p) is a substructure of A, ran(p) is a substructure of B, and p is an isomorphism of its domain onto its range; and
- If p ∈ P, a ∈ A, b ∈ B, then there exist r, s ∈ P both extending p such that a ∈ dom(r), b ∈ ran(s) ("back and forth" property).
If a partial isomorphism exists between A
and B, we say that
A and B are
partially isomorphic and write A
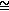 p B. We
then have
p B. We
then have
Karp's Partial Isomorphism Theorem.
For any similar structures A, B, A ≡∞ω B ⇔ Ap B.
There is also a version of Scott's isomorphism theorem for
 (∞,ω),
namely,
(∞,ω),
namely,
(2.2) Given any structure A, there is an(∞,ω)-sentence σ such that, for all structures B, A
p B ⇔ B
σ.
Partial isomorphism and (∞,ω)-equivalence are related to the notion of Boolean isomorphism. To define this we need to introduce the idea of a Boolean-valued model of set theory. Given a complete Boolean algebra B, the universe V(B) of B-valued sets, also known as the B-extension of the universe V of sets, is obtained by first defining, recursively on α,
Vα(B) = {x: x is a functionrange(x) ⊆ B
∃ξ<α[domain(x) ⊆ Vξ(B)]}
and then setting
V(B) = {x: ∃α(x ∈ Vα(B))}.
Members of V(B) are called B-valued
sets. It is now easily seen that a B-valued set is
precisely a B-valued function with domain a set of
B-valued sets. Now let L be the first-order
language of set theory and let
L(B) be the language obtained by
adding to L a name for each element of
V(B) (we shall use the same symbol for the
element and its name). One can now construct a mapping
[·](B) of the (sentences of the) language
L(B) into B: for each
sentence σ of L(B), the
element [σ](B) of B is the "Boolean
truth value" of σ in V(B). This
mapping [·](B) is defined so as to send all
the theorems of Zermelo-Fraenkel set theory to the top element 1 of
B, i.e., to "truth"; accordingly,
V(B) may be thought of as a
Boolean-valued model of set theory. In general, if
[σ](B) = 1, we say that σ is
valid in V(B), and write
V(B)
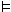 σ.
σ.
Now each x ∈ V has a canonical representative x in V(B), satisfying
x = y iff V(B)We say that two similar structures A, B are Boolean isomorphic, written Ax = y
x ∈ y iff V(B)x ∈ y
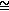 b B, if, for
some complete Boolean algebra B, we have
V(B)
b B, if, for
some complete Boolean algebra B, we have
V(B)
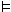 A
A
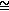 B, that is, if there is a Boolean
extension of the universe of sets in which the canonical
representatives of A and
B are isomorphic with Boolean value 1. It can
then be shown that:
B, that is, if there is a Boolean
extension of the universe of sets in which the canonical
representatives of A and
B are isomorphic with Boolean value 1. It can
then be shown that:
(2.3) A ≡∞ω B ⇔ AThis result can be strengthened through category-theoretic formulation. For this we require the concept of a(n) (elementary) topos. To introduce this concept, we start with the familiary category of Set of sets and mappings. Set has the following key properties:b B.
- There is a "terminal" object 1 such that, for any object X, there is a unique map X → 1 (for 1 we may take any one-element set, in particular, {0}).
- Any pair of objects X,Y has a Cartesian product X × Y.
- for any pair of objects one can form the "exponential" object YX of all maps from X → Y.
- There is a "truth-value" object Ω such that for each object X there is a natural correspondence between subobjects (subsets) of X and maps X → Ω. (For Ω we may take the set 2 = {0,1}; maps X → Ω are then characteristic functions on X.)
All four of these conditions can be formulated in category-theoretic language — a category satisfying them is called a topos. The category Set is a topos; so also are (i) the category Set(B) of Boolean-valued sets and mappings in any Boolean extension V(B) of the universe of sets; (ii) the category of sheaves of sets on a topological space; (iii) the category of all diagrams of maps of sets
X0 → X1 → X2 → …
The objects of each of these categories may be regarded as sets which are varying in some manner: in case (i) over a Boolean algebra; in case (ii) over a topological space; in case (iii) over (discrete) time. A topos may be conceived, then, as a universe of "variable" sets. The familiar category Set is the special limiting case of a topos in which the "variation" of the objects has been reduced to zero.
Just as in set theory, "logical operators" can be defined on the
truth-value object in any topos. These are maps ¬: Ω →
Ω;
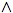 ,
,
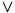 , ⇒: Ω × Ω → Ω
corresponding to the logical operations of negation, conjunction,
disjunction and implication. With these operations, Ω becomes a
Heyting algebra, thus embodying in general the laws not of classical
but of intutionistic logic. In this sense intuitionistic logic is
"internalized" in a topos: intuitionistic logic is the logic of
variable sets. (Of course, classical logic is internalized in certain
toposes, for instance Set and
Set(B) for any complete Boolean
algebra B.)
, ⇒: Ω × Ω → Ω
corresponding to the logical operations of negation, conjunction,
disjunction and implication. With these operations, Ω becomes a
Heyting algebra, thus embodying in general the laws not of classical
but of intutionistic logic. In this sense intuitionistic logic is
"internalized" in a topos: intuitionistic logic is the logic of
variable sets. (Of course, classical logic is internalized in certain
toposes, for instance Set and
Set(B) for any complete Boolean
algebra B.)
Any topos may be conceived as possible "universe of discourse" in
which mathematical assertions may be interpreted and mathematical
constructions may be performed. Mathematical assertions are rendered
interpretable in a topos
 by
expression within
by
expression within
 's
internal language — a type-theoretic version of the
usual language of set theory. In a manner analogous to Boolean-valued
validity, one can introduce an appropriate notion of validity in
's
internal language — a type-theoretic version of the
usual language of set theory. In a manner analogous to Boolean-valued
validity, one can introduce an appropriate notion of validity in
 of a sentence σ of its
internal language. Again, we write
of a sentence σ of its
internal language. Again, we write
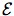
 σ for
"σ is valid in
σ for
"σ is valid in
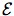 ".
".
A topos
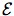 is said to be
full if, for any set I, the I-fold
copower[3]
is said to be
full if, for any set I, the I-fold
copower[3]
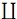 I1 of its terminal object exists
in
I1 of its terminal object exists
in
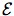 .
.
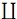 I1 may be thought of as the
canonical representative in
I1 may be thought of as the
canonical representative in
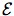 of
the set I; accordingly, we write it simply as
I. (In V(B) this coincides
with I as previously defined.) All the toposes
mentioned above are full.
of
the set I; accordingly, we write it simply as
I. (In V(B) this coincides
with I as previously defined.) All the toposes
mentioned above are full.
Now let
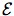 be a full topos. If
A = (A, R, …) is a
structure, write A for
(A, R, …). Two structures
A and B are said to
be topos isomorphic, written A
be a full topos. If
A = (A, R, …) is a
structure, write A for
(A, R, …). Two structures
A and B are said to
be topos isomorphic, written A
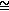 t
B, if, for some topos
t
B, if, for some topos
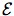 defined over the category of sets, we have
defined over the category of sets, we have
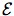
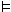 A
A
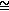 B. In other words two structures are topos isomorphic
if their canonical representatives are isomorphic in the internal
language of some topos. It can then be shown that
B. In other words two structures are topos isomorphic
if their canonical representatives are isomorphic in the internal
language of some topos. It can then be shown that
(2.4) A ≡∞ω B ⇔ At B.
Accordingly (∞,ω)-equivalence may be regarded as isomorphism in the extremely general context of universes of "variable" sets. In this respect (∞,ω)-equivalence is an "invariant" notion of isomorphism.
3. The Compactness Property
As we have seen, the compactness theorem in its usual form fails for all infinitary languages. Nevertheless, it is of some interest to determine whether infinitary languages satisfy some suitably modified version of the theorem. This so-called compactness problem turns out to have a natural connection with purely set-theoretic questions involving "large" cardinal numbers.
We construct the following definition. Let κ be an infinite
cardinal. A language L is said to be
κ-compact (resp. weakly
κ-compact) if whenever Δ is a set of
L-sentences (resp. a set of
L-sentences of cardinality ≤ κ) and each
subset of Δ of cardinality < κ has a model, so does
Δ. Notice that the usual compactness theorem for
 is precisely the assertion that
is precisely the assertion that
 is ω-compact. One reason for
according significance to the κ-compactness property is the
following. Call L κ-complete (resp. weakly
κ-complete) if there is a deductive system
P for L with deductions of
length < κ such that, if Δ is a
P-consistent[4]
set of
L-sentences (resp. such that |Δ| ≤ κ),
then Δ has a model. Observe that such a
P will be adequate for deductions from
arbitrary sets of premises (of cardinality ≤ κ) in the sense
of §2. It is easily seen that if L is
κ-complete or weakly κ-complete, then L is
κ-compact or weakly κ-compact. Thus, if we can show that a
given language is not (weakly) κ-compact, then there can
be no deductive system for it with deductions of length < κ
adequate for deductions from arbitrary sets of premises (of cardinality
≤ κ).
is ω-compact. One reason for
according significance to the κ-compactness property is the
following. Call L κ-complete (resp. weakly
κ-complete) if there is a deductive system
P for L with deductions of
length < κ such that, if Δ is a
P-consistent[4]
set of
L-sentences (resp. such that |Δ| ≤ κ),
then Δ has a model. Observe that such a
P will be adequate for deductions from
arbitrary sets of premises (of cardinality ≤ κ) in the sense
of §2. It is easily seen that if L is
κ-complete or weakly κ-complete, then L is
κ-compact or weakly κ-compact. Thus, if we can show that a
given language is not (weakly) κ-compact, then there can
be no deductive system for it with deductions of length < κ
adequate for deductions from arbitrary sets of premises (of cardinality
≤ κ).
It turns out, in fact, that most languages
 (κ,λ)
fail to be even weakly
κ-compact, and, for those that are, κ must be an
exceedingly large cardinal. We shall need some
definitions.
(κ,λ)
fail to be even weakly
κ-compact, and, for those that are, κ must be an
exceedingly large cardinal. We shall need some
definitions.
An infinite cardinal κ is said to be weakly inaccessible if
(a) λ < κ → λ+ < κ, (where λ+ denotes the cardinal successor of λ), andIf in addition(b) |I| < κ and λi < κ (for all i ∈ I) ⇒ ∑i∈I λi < κ.
(c) λ < κ ⇒ 2λ < κ ,then κ is said to be (strongly)inaccessible. Since
 0 is inaccessible,
it is normal practice to confine attention to those inaccessible, or
weakly inaccessible, cardinals that exceed
0 is inaccessible,
it is normal practice to confine attention to those inaccessible, or
weakly inaccessible, cardinals that exceed
 0. Accordingly, inaccessible or weakly
inaccessible cardinals will always be taken to be uncountable.
It is clear that such cardinals—if they exist—must be
extremely large; and indeed the Gödel incompleteness theorem
implies that the existence of even weakly inaccessible cardinals cannot
be proved from the usual axioms of set theory.
0. Accordingly, inaccessible or weakly
inaccessible cardinals will always be taken to be uncountable.
It is clear that such cardinals—if they exist—must be
extremely large; and indeed the Gödel incompleteness theorem
implies that the existence of even weakly inaccessible cardinals cannot
be proved from the usual axioms of set theory.
Let us call a cardinal κ compact (resp. weakly
compact) if the language
 (κ,κ)
is κ-compact (resp. weakly
κ-compact). Then we have the following results:
(κ,κ)
is κ-compact (resp. weakly
κ-compact). Then we have the following results:
(3.1)Let Constr stand for Gödel's axiom of constructibility; recall that Constr is consistent with the usual axioms of set theory.0 is compact. This is, of course, just a succinct way of expressing the compactness theorem for first-order languages.
(3.2) κ is weakly compact ⇒
(κ,ω) is weakly κ-compact ⇒ κ is weakly inaccessible. Accordingly, it is consistent (with the usual axioms of set theory) to assume that no language
(κ,ω) with κ ≥ ω1 is weakly κ-compact, or, a fortiori, weakly κ-complete.
(3.3) Suppose κ is inaccessible. Then κ is weakly compact ⇔
(κ,ω) is weakly κ-compact. Also, Also κ is weakly compact ⇒ there is a set of κ inaccessibles before κ. Thus a weakly compact inaccessible cardinal is exceedingly large; in particular it cannot be the first, second, …, nth, … inaccessible.
(3.4) κ is compact ⇒ κ is inaccessible. (But, by the result immediately above, the converse fails.)
(3.5) If Constr holds, then there are no compact cardinals.(3.6) Assume Constr and let κ be inaccessible. Then κ is weakly compact ⇔
(ω1,ω) is weakly κ-compact for all
.
(3.7) If Constr holds, then there are no cardinals κ for which
(ω1,ω) is compact. Accordingly, it is consistent with the usual axioms of set theory to suppose that there is no cardinal κ such that all languages
(ω1,ω) are κ-complete. This result is to be contrasted with the fact that all first-order languages are ω-complete.
The import of these results is that the compactness theorem fails
very badly for most languages
 (κ,λ)
with κ ≥
ω1.
(κ,λ)
with κ ≥
ω1.
Some historical remarks are in order here. In the 1930s mathematicians investigated various versions of the so-called measure problem for sets, a problem which arose in connection with the theory of Lebesgue measure on the continuum. In particular, the following very simple notion of measure was formulated. If X is a set, a (countably additive two-valued nontrivial) measure on X is a map μ on the power set PX to the set {0, 1} satisfying:
(a) μ(X) = 1,(b) μ({x}) = μ(Ø) = 0 for all x ∈X, and
(c) if A is any countable family of mutually disjoint subsets of X, then μ(
A) = ∑{μ(Y) : Y ∈ A}.
Obviously, whether a given set supports such a measure depends only on its cardinality, so it is natural to define a cardinal κ to be measurable if all sets of cardinality κ support a measure of this sort. It was quickly realized that a measurable cardinal must be inaccessible, but the falsity of the converse was not established until the 1960s when Tarski showed that measurable cardinals are weakly compact and his student Hanf showed that the first, second, etc. inaccessibles are not weakly compact (cf. (3.3)). Although the conclusion that measurable cardinals must be monstrously large is now normally proved without making the detour through weak compactness and infinitary languages, the fact remains that these ideas were used to establish the result in the first instance.
4. Incompleteness of Infinite-Quantifier Languages
Probably the most important result about first-order languages is the Gödel completeness theorem which of course says that the set of all valid formulas of any first-order language can be generated from a simple set
of axioms by means of a few straightforward rules of inference. A major
consequence of this theorem is that, if the formulas of
can be generated from a simple set
of axioms by means of a few straightforward rules of inference. A major
consequence of this theorem is that, if the formulas of
 are coded as natural numbers in some
constructive way, then the set of (codes of) valid sentences is
recursively enumerable. Thus, the completeness of a
first-order language implies that the set of its valid sentences is
definable in a particularly simple way. It would accordingly
seem reasonable, given an arbitrary language
L, to turn this implication around and suggest that,
if the set of valid L-sentences is not
definable in some simple fashion, then no meaningful
completeness result can be established for L, or, as
we shall say, that L is incomplete. In this
section we are going to employ this suggestion in sketching a proof
that "most" infinite quantifier languages are incomplete in
this sense.
are coded as natural numbers in some
constructive way, then the set of (codes of) valid sentences is
recursively enumerable. Thus, the completeness of a
first-order language implies that the set of its valid sentences is
definable in a particularly simple way. It would accordingly
seem reasonable, given an arbitrary language
L, to turn this implication around and suggest that,
if the set of valid L-sentences is not
definable in some simple fashion, then no meaningful
completeness result can be established for L, or, as
we shall say, that L is incomplete. In this
section we are going to employ this suggestion in sketching a proof
that "most" infinite quantifier languages are incomplete in
this sense.
Let us first introduce the formal notion of definability as follows. If L is a language, A an L-structure, and X a subset of the domain A of A, we say that X is definable in A by a formula φ(x, y1,…,yn) of L if there is a sequence a1,…,an of elements of A such that X is the subset of all elements x ∈ A for which φ(x, a1,…,an) holds in A.
Now write Val(L) for the set of all the valid L-sentences, i.e., those that hold in every L-structure. In order to assign a meaning to the statement "Val(L) is definable", we have to specify
(i) a structure C(L)—the coding structure for L;Then, if we identify Val(L) with its image in C(L) under the coding map, we shall interpret the statement "Val(L) is definable" as the statement "Val(L), regarded as a subset of the domain of C(L), is definable in C(L) by a formula of L."(ii) a particular one-one map—the coding map—of the set of formulas of L into the domain of C(L).
For example, when L is the first-order
language
 of arithmetic, Gödel
originally used as coding structure the standard model of
arithmetic
of arithmetic, Gödel
originally used as coding structure the standard model of
arithmetic
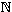 and as coding map the well-known
function obtained from the prime factorization theorem for natural
numbers. The recursive enumerability of Val(
and as coding map the well-known
function obtained from the prime factorization theorem for natural
numbers. The recursive enumerability of Val( ) then means simply that the set of
codes ("Gödel numbers") of members of Val(
) then means simply that the set of
codes ("Gödel numbers") of members of Val( ) is definable in
) is definable in
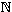 by an
by an
 -formula
of
the form ∃yφ(x, y), where φ(x,
y) is a recursive formula.
-formula
of
the form ∃yφ(x, y), where φ(x,
y) is a recursive formula.
Another, equivalent, coding structure for the first-order language of arithmetic is the structure[5] <H(ω), ∈| H(ω)> of hereditarily finite sets, where a set x is hereditarily finite if x, its members, its members of members, etc., are all finite. This coding structure takes account of the fact that first-order formulas are naturally regarded as finite sets.
Turning now to the case in which L is an infinitary
language
 (κ,λ),
what
would be a suitable coding structure in this case? We remarked at
the beginning that infinitary languages were suggested by the
possibility of thinking of formulas as set-theoretical objects, so let
us try to obtain our coding structure by thinking about what kind of
set-theoretical objects we should take infinitary formulas to be. Given
the fact that, for each
φ∈Form(κ,λ), φ and its
subformulas, subsubformulas, etc., are all of length <
κ,[6]
a moment's reflection reveals that
formulas of
(κ,λ),
what
would be a suitable coding structure in this case? We remarked at
the beginning that infinitary languages were suggested by the
possibility of thinking of formulas as set-theoretical objects, so let
us try to obtain our coding structure by thinking about what kind of
set-theoretical objects we should take infinitary formulas to be. Given
the fact that, for each
φ∈Form(κ,λ), φ and its
subformulas, subsubformulas, etc., are all of length <
κ,[6]
a moment's reflection reveals that
formulas of
 (κ,λ)
"correspond"
to sets x hereditarily of cardinality <
κ in the sense that x, its members, its members of
members, etc., are all of cardinality < κ. The collection of
all such sets is written H(κ). H(ω) is
the collection of hereditarily finite sets introduced above,
and H(ω1) that of all hereditarily
countable sets.
(κ,λ)
"correspond"
to sets x hereditarily of cardinality <
κ in the sense that x, its members, its members of
members, etc., are all of cardinality < κ. The collection of
all such sets is written H(κ). H(ω) is
the collection of hereditarily finite sets introduced above,
and H(ω1) that of all hereditarily
countable sets.
For simplicity let us suppose that the only extralogical symbol of
the base language
 is the binary
predicate symbol ∈ (the discussion is easily extended to
the case in which
is the binary
predicate symbol ∈ (the discussion is easily extended to
the case in which
 contains
additional extralogical symbols). Guided by the remarks above, as
coding structure for
contains
additional extralogical symbols). Guided by the remarks above, as
coding structure for
 (κ,λ)
we take the structure,
(κ,λ)
we take the structure,
(κ) =df <H(κ), ∈| H(κ)>.
Now we can define the coding map of
Form(κ,λ) into
 (κ).
First, to each basic symbol s
of
(κ).
First, to each basic symbol s
of
 (κ,λ) we assign a
code object
(κ,λ) we assign a
code object
 s
s ∈ H(κ) as
follows. Let {vξ: ξ < κ} be an
enumeration of the individual variables of
∈ H(κ) as
follows. Let {vξ: ξ < κ} be an
enumeration of the individual variables of
 (κ,λ).
(κ,λ).
Then, to each φ ∈ Form(κ,λ) we assign the code object
Symbol Code Object Notation ¬ 1 ¬
2 3 ∃ 4 ∃
∈ 5 ∈
= 6 =
vξ <0,ξ> vξ
 φ
φ
 recursively as follows:
recursively as follows:
for φ, ψ ∈ Form(κ,λ),vξ = vη
=df <
vξ
,
=
,
vη
>,
vξ ∈ vη
=df <
vξ
,
∈
,
vη
>;
and finally if Φ ⊆ Form(κ,λ) with | Φ | < κ,φ
ψ
=df <
φ
,
,
ψ
>
¬φ
=df <
¬
,
φ
>
∃Xφ
=df <
∃
, {
x
: x ∈ X},
φ
>;
Φ
=df <
, {
φ
: φ ∈ Φ}>.
The map φ
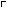 φ
φ from Form(κ,λ) into
H(κ) is easily seen to be one-one and is the required
coding map. Accordingly, we agree to identify Val(
from Form(κ,λ) into
H(κ) is easily seen to be one-one and is the required
coding map. Accordingly, we agree to identify Val( (κ,λ)) with its image in
H(κ) under this coding map.
(κ,λ)) with its image in
H(κ) under this coding map.
When is Val( (κ,λ)) a definable subset of
(κ,λ)) a definable subset of
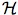 (κ)?
In order to answer this
question we require the following definitions.
(κ)?
In order to answer this
question we require the following definitions.
An
 -formula
is called a
Δ0-formula if it is equivalent to a formula
in which all quantifiers are of the form
∀x∈y or ∃x∈y
(i.e., ∀x(x∈y → …)
or ∃x(x∈y
-formula
is called a
Δ0-formula if it is equivalent to a formula
in which all quantifiers are of the form
∀x∈y or ∃x∈y
(i.e., ∀x(x∈y → …)
or ∃x(x∈y
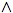 …)). An
…)). An
 -formula
is a Σ1-formula if
it is equivalent to one which can be built up from atomic formulas and
their negations using only the logical operators
-formula
is a Σ1-formula if
it is equivalent to one which can be built up from atomic formulas and
their negations using only the logical operators
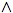 ,
,
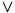 ,
∀x∈y, ∃x. A subset
X of a set A is said to be Δ0 (resp.
Σ1) on A if it is definable in the structure
<A, ∈| A> by a Δ0- (resp.
Σ1-) formula of
,
∀x∈y, ∃x. A subset
X of a set A is said to be Δ0 (resp.
Σ1) on A if it is definable in the structure
<A, ∈| A> by a Δ0- (resp.
Σ1-) formula of
 .
.
For example, if we identify the set of natural numbers with the set H(ω) of hereditarily finite sets in the usual way, then for each X ⊆ H(ω) we have:
X is Δ0 on H(ω) ⇔ X is recursiveThus the notions of Δ0- and Σ1-set may be regarded as generalizations of the notions of recursive and recursively enumerable set, respectively.X is Σ1 on H(ω) ⇔ X is recursively enumerable.
The completeness theorem for
 implies
that Val(
implies
that Val( )
— regarded as a subset of H(ω) — is
recursively enumerable, and hence Σ1 on
H(ω). Similarly, the completeness theorem for
)
— regarded as a subset of H(ω) — is
recursively enumerable, and hence Σ1 on
H(ω). Similarly, the completeness theorem for
 (ω1,ω) (see
§2) implies that Val(
(ω1,ω) (see
§2) implies that Val( (ω1,ω)) — regarded as a
subset of H(ω1) — is
Σ1 on H(ω1). However, this
pleasant state of affairs collapses completely as soon as
(ω1,ω)) — regarded as a
subset of H(ω1) — is
Σ1 on H(ω1). However, this
pleasant state of affairs collapses completely as soon as
 (ω1,ω1) is reached.
For one can prove
(ω1,ω1) is reached.
For one can prove
Scott's Undefinability Theorem forThis theorem is proved in much the same way as the well-known result that the set of (codes of) valid sentences of the second-order language of arithemetic(ω1,ω1). Val(
(ω1,ω1)) is not definable in
(ω1) even by an
(ω1,ω1)-formula; hence a fortiori Val(
(ω1,ω1)) is not Σ1 on H(ω1).
 2 is
not second-order definable in its coding structure
2 is
not second-order definable in its coding structure
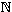 .
To get this latter result, one first observes that
.
To get this latter result, one first observes that
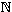 is characterized by a single
is characterized by a single
 2-sentence, and then shows
that, if the result were false, then "truth in
2-sentence, and then shows
that, if the result were false, then "truth in
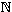 "
for
"
for
 2-sentences would be definable by an
2-sentences would be definable by an
 2-formula, thereby
violating Tarski's theorem on the undefinability of truth.
2-formula, thereby
violating Tarski's theorem on the undefinability of truth.
Accordingly, to prove Scott's undefinability theorem along the above lines, one needs to establish:
(4.1) Characterizability of the coding structure(4.1) is proved by analyzing the set-theoretic definition of(ω1) in
(ω1,ω1): there is an
(ω1,ω1)-sentence τ0 such that, for all
-structures A,
Aτ0 ⇔ A
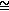
(ω1).
(4.2) Undefinability of truth for
(ω1,ω1)-sentences in the coding structure: there is no
(ω1,ω1)-formula φ(v0) such that, for all
(ω1, ω1)-sentences σ,
(ω1)
σ↔φ(
σ
).
(4.3) There is a term t(v0, v1) of
(ω1,ω1) such that, for each pair of sentences σ, τ of
(ω1,ω1),
(ω1)
[t(
σ
,
τ
) =
σ → τ
].
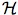 (ω1) and showing
that it can be "internally" formulated in
(ω1) and showing
that it can be "internally" formulated in
 (ω1,ω1). (4.2) is
established in much the same way as Tarski's theorem on the
undefinability of truth for first- or second-order languages. (4.3) is
obtained by formalizing the definition of the coding map σ
(ω1,ω1). (4.2) is
established in much the same way as Tarski's theorem on the
undefinability of truth for first- or second-order languages. (4.3) is
obtained by formalizing the definition of the coding map σ
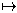
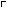 σ
σ in
in
 (ω1,ω1).
(ω1,ω1).
Armed with these facts, we can obtain Scott's undefinability theorem
in the following way. Suppose it were false; then there would be
an
 (ω1,ω1)-formula
θ(v0) such that, for all
(ω1,ω1)-formula
θ(v0) such that, for all
 (ω1,ω1)-sentences
σ,
(ω1,ω1)-sentences
σ,
(4.4)Let τ0 be the sentence given in (4.1). Then we have, for all(ω1)
θ(
σ
) iff σ ∈ Val(
(ω1,ω1)).
 (ω1,ω1)-sentences
σ,
(ω1,ω1)-sentences
σ,
so that, by (4.4),(ω1)
σ iff (τ0 → σ) ∈ Val(
(ω1,ω1)),
If t is the term given in (4.3), it would follow that(ω1)
σ iff
(ω1)
θ(
τ0 → σ
).
Now write φ(v0) for the(ω1)
σ↔θ(t(
τ0
,
σ
)).
 (ω1,ω1)-formula
θ(t(
(ω1,ω1)-formula
θ(t(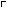 τ0
τ0 ,
,
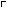 σ
σ )). Then
)). Then
contradicting (4.2), and completing the proof.(ω1)
σ↔φ(
σ
),
Thus Val( (ω1,ω1)) is not
definable even by an
(ω1,ω1)) is not
definable even by an
 (ω1,ω1)-formula,
so a fortiori
(ω1,ω1)-formula,
so a fortiori
 (ω1,ω1) is
incomplete. Similar arguments show that Scott's undefinability theorem
continues to hold when ω1 is replaced by any successor
cardinal κ+; accordingly the languages
(ω1,ω1) is
incomplete. Similar arguments show that Scott's undefinability theorem
continues to hold when ω1 is replaced by any successor
cardinal κ+; accordingly the languages
 (κ+,κ+) are all
incomplete.[7]
(κ+,κ+) are all
incomplete.[7]
5. Sublanguages of
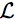 (ω1,ω) and the Barwise Compactness Theorem
(ω1,ω) and the Barwise Compactness Theorem
Given what we now know about infinitary languages, it would seem
that
 (ω1,ω) is
the only one to be reasonably well behaved. On the other hand, the
failure of the compactness theorem to generalize to
(ω1,ω) is
the only one to be reasonably well behaved. On the other hand, the
failure of the compactness theorem to generalize to
 (ω1,ω) in any
useful fashion is a severe drawback as far as applications are
concerned. Let us attempt to analyze this failure in more detail.
(ω1,ω) in any
useful fashion is a severe drawback as far as applications are
concerned. Let us attempt to analyze this failure in more detail.
Recall from §4 that we may code the formulas of a first-order
language
 as hereditarily finite
sets, i.e., as members of H(ω). In that case each finite
set of (codes of)
as hereditarily finite
sets, i.e., as members of H(ω). In that case each finite
set of (codes of)
 -sentences
is
also a member of H(ω), and it follows that the
compactness theorem for
-sentences
is
also a member of H(ω), and it follows that the
compactness theorem for
 can be
stated in the form:
can be
stated in the form:
(5.1) If Δ ⊆ Sent(Now it is well-known that (5.1) is an immediate consequence of the generalized completeness theorem for) is such that each subset Δ0 ⊆ Δ, Δ0 ∈ H(ω) has a model, so does Δ.
 ,
which, stated in a form similar to that of (5.1),
becomes the assertion:
,
which, stated in a form similar to that of (5.1),
becomes the assertion:
(5.2) If Δ ⊆ Sent(In §2 we remarked that the compactness theorem for) and σ ∈ Sent(
) satisfy Δ
σ, then there is a deduction D of σ from Δ such that D ∈ H(ω).[8]
 (ω1,ω) fails
very strongly; in fact, we constructed a set Γ ⊆
Sent(ω1,ω) such that
(ω1,ω) fails
very strongly; in fact, we constructed a set Γ ⊆
Sent(ω1,ω) such that
(5.3) Each countable subset of Γ has a model but Γ does not.Recall also that we introduced the notion of deduction in
 (ω1,ω); since
such deductions are of countable length it quickly follows from (5.3)
that
(ω1,ω); since
such deductions are of countable length it quickly follows from (5.3)
that
(5.4) There is a sentence[9]σ ∈ Sent(ω1,ω) such that ΓNow the formulas ofσ, but there is no deduction of σ in
(ω1,ω) from Γ.
 (ω1, ω) can be coded as members
of
(ω1, ω) can be coded as members
of
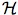 (ω1), and it
is clear that
(ω1), and it
is clear that
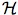 (ω1) is closed under the formation of
countable subsets and sequences. Accordingly (5.3) and (5.4) may be
written:
(ω1) is closed under the formation of
countable subsets and sequences. Accordingly (5.3) and (5.4) may be
written:
(5.3 bis) Each Γ0 ⊆ Γ such that Γ0 ∈It follows that (5.1) and (5.2) fail when "(ω1) has a model, but Γ does not;
(5.4 bis) There is a sentence σ ∈ Sent(ω1,ω) such that Γ
σ, but there is no deduction D ∈ H(ω1) of σ from Γ.
 " is replaced by
"
" is replaced by
" (ω1,ω)" and
"
(ω1,ω)" and
"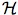 (ω)" by
"
(ω)" by
"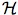 (ω1)". Moreover, it can be shown that
the set Γ ⊆
Sent(ω1,ω) in (5.3
bis) and (5.4 bis) may be taken to be
Σ1 on H(ω1). Thus the
compactness and generalized completeness theorems fail even for
Σ1-sets of
(ω1)". Moreover, it can be shown that
the set Γ ⊆
Sent(ω1,ω) in (5.3
bis) and (5.4 bis) may be taken to be
Σ1 on H(ω1). Thus the
compactness and generalized completeness theorems fail even for
Σ1-sets of
 (ω1, ω)-sentences.
(ω1, ω)-sentences.
We see from (5.4 bis) that the reason why the generalized
completeness theorem fails for Σ1-sets in
 (ω1,ω) is
that, roughly speaking, H(ω1) is not "closed"
under the formation of deductions from Σ1-sets of
sentences in H(ω1). So in order to remedy
this it would seem natural to replace H(ω1)
by sets A which are, in some sense, closed under the formation
of such deductions, and then to consider just those formulas whose
codes are in A.
(ω1,ω) is
that, roughly speaking, H(ω1) is not "closed"
under the formation of deductions from Σ1-sets of
sentences in H(ω1). So in order to remedy
this it would seem natural to replace H(ω1)
by sets A which are, in some sense, closed under the formation
of such deductions, and then to consider just those formulas whose
codes are in A.
We now give a sketch of how this can be done.
First, we identify the symbols and formulas of
 (ω1,ω) with
their codes in H(ω1), as in §4. For each
countable
transitive[10]
set A, let
(ω1,ω) with
their codes in H(ω1), as in §4. For each
countable
transitive[10]
set A, let
We say thatA = Form(
(ω1,ω)) ∩ A.
 A is a sublanguage of
A is a sublanguage of
 (ω1,ω) if the
following conditions are satisfied:
(ω1,ω) if the
following conditions are satisfied:
(i)The notion of deduction in⊆
A
(ii) if φ, ψ ∈
A, then φ
ψ ∈
A and ¬φ ∈
A
(iii) if φ ∈
A and x ∈ A, then ∃xφ ∈
A
(iv) if φ(x) ∈
A and y ∈ A, then φ(y) ∈
A
(v) if φ ∈
A, every subformula of φ is in
A
(vi) if Φ ⊆
A and Φ ∈ A, then
Φ ∈
A.
 A is defined in the customary way;
if Δ is a set of sentences of
A is defined in the customary way;
if Δ is a set of sentences of
 A and φ ∈
A and φ ∈
 A, then a
deduction of φ from Δ in
A, then a
deduction of φ from Δ in
 A is a deduction of φ from
Δ in
A is a deduction of φ from
Δ in
 (ω1,
ω) every formula of which is in
(ω1,
ω) every formula of which is in
 A. We say that φ is
deducible from Δ in
A. We say that φ is
deducible from Δ in
 A if there is a deduction
D of φ from Δ in
A if there is a deduction
D of φ from Δ in
 A; under these
conditions we write Δ
A; under these
conditions we write Δ
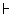 A φ. In general,
D will not be a member of A; in
order to ensure that such a deduction can be found in A it
will be necessary to impose further conditions on A.
A φ. In general,
D will not be a member of A; in
order to ensure that such a deduction can be found in A it
will be necessary to impose further conditions on A.
Let A be a countable transitive set such that
 A is a
sublanguage of
A is a
sublanguage of
 (ω1, ω) and let Δ be a set
of sentences of
(ω1, ω) and let Δ be a set
of sentences of
 A. We say that A (or, by
abuse of terminology,
A. We say that A (or, by
abuse of terminology,
 A) is Δ-closed if,
for any formula φ of
A) is Δ-closed if,
for any formula φ of
 A such that Δ
A such that Δ
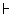 A φ, there is a
deduction D of φ from Δ such that
D ∈ A. It can be shown that the
only countable language which is Δ-closed for arbitrary
Δ is the first-order language
A φ, there is a
deduction D of φ from Δ such that
D ∈ A. It can be shown that the
only countable language which is Δ-closed for arbitrary
Δ is the first-order language
 ,
i.e., when A = H(ω). However
J. Barwise discovered that there are countable sets A ⊆
H(ω1) whose corresponding languages
,
i.e., when A = H(ω). However
J. Barwise discovered that there are countable sets A ⊆
H(ω1) whose corresponding languages
 A differ
from
A differ
from
 and yet are Δ-closed
for all Σ1-sets of sentences
Δ. Such sets A are called admissible sets;
roughly speaking, they are extensions of the hereditarily finite sets
in which recursion theory—and hence proof theory—are still
possible.[11]
and yet are Δ-closed
for all Σ1-sets of sentences
Δ. Such sets A are called admissible sets;
roughly speaking, they are extensions of the hereditarily finite sets
in which recursion theory—and hence proof theory—are still
possible.[11]
From Barwise's result one obtains immediately the
Barwise Compactness Theorem. Let A be a countable admissible set and let Δ be a set of sentences ofThe presence of "Σ1" here indicates that this theorem is a generalization of the compactness theorem for recursively enumerable sets of sentences.A which is Σ1 on A. If each Δ′ ⊆ Δ such that Δ′ ∈ A has a model, then so does Δ.
Another version of the Barwise compactness theorem, useful for constructing models of set theory, is the following. Let ZFC be the usual set of axioms for Zermelo-Fraenkel set theory, including the axiom of choice. Then we have:
5.5. Theorem. Let A be a countable transitive set such that A = <A, ∈| A> is a model of ZFC. If Δ is a set of sentences ofTo conclude, we give a simple application of this theorem. Let A = <A, ∈| A> be a model of ZFC. A model B = <B, E> of ZFC is said to be a proper end-extension of A if (i) A ⊆ B, (ii) A ≠ B, (iii) a ∈ A, b ∈ B, bEa ⇒ b∈A. Thus a proper end-extension of a model of ZFC is a proper extension in which no "new" element comes "before" any "old" element. As our application of 5.5 we proveA which is definable in A by a formula of the language of set theory and if each Δ′ ⊆ Δ such that Δ′ ∈ A has a model, so does Δ.
5.6. Theorem. Each countable transitive model of ZFC has a proper end-extension.The reader will quickly see that the first-order compactness theorem will not yield this result.Proof. Let A = <A, ∈| A> be a transitive model of ZFC and let
be the first-order language of set theory augmented by a name a for each a ∈ A, and an additional constant c. Let Δ be the set of
A-sentences comprising:
It is easily shown that Δ is a subset of A which is definable in A by a formula of the language of set theory. Also, each subset Δ′ ⊆ Δ such that Δ′ ∈ A has a model. For the set C of all a ∈ A for which a occurs in Δ′ belongs to A — since Δ′ does — and so, if we interpret c as any member of the (necessarily nonempty) set A − C, then A is a model of Δ′. Accordingly, (5.5) implies that Δ has a model <B, E>. If we interpret each constant a as the element a ∈ A, then <B, E> is a proper end-extension of A. The proof is complete.
- all axioms of ZFC;
- c ≠ a, for each a ∈ A;
- ∀x(x ∈ a →
b∈a x = b), for each a ∈ A;
- a ∈ b, for each a ∈ b ∈ A.
[Supplement: Definition of the Concept of Admissible Set
6. Historical and Bibliographical Remarks
§§1 and 2. Infinitary propositional and predicate languages seem to have made their first explicit appearance in print with the papers of Scott and Tarski [1958] and Tarski [1958]. The completeness theorem for (ω1,ω), as well as for other
infinitary languages, was proved by Karp [1964]. The Hanf number
calculations for
(ω1,ω), as well as for other
infinitary languages, was proved by Karp [1964]. The Hanf number
calculations for
 (ω1,ω) were first performed by
Morley [1965]. The nondefinability of well-orderings in
finite-quantifier languages was proved by Karp [1965] and Lopez-Escobar
[1966]. The interpolation theorem for
(ω1,ω) were first performed by
Morley [1965]. The nondefinability of well-orderings in
finite-quantifier languages was proved by Karp [1965] and Lopez-Escobar
[1966]. The interpolation theorem for
 (ω1,ω) was proved by
Lopez-Escobar [1965] and Scott's isomorphism theorem for
(ω1,ω) was proved by
Lopez-Escobar [1965] and Scott's isomorphism theorem for
 (ω1,ω) by
Scott [1965].
(ω1,ω) by
Scott [1965].
Karp's partial isomorphism theorem was first proved in Karp [1965]; see also Barwise [1973]. Result (2.2) appears in Chang [1968], result (2.3) in Ellentuck [1976] and result (2.4) in Bell [1981].
§3. Results (3.2) and (3.3) are due to Hanf [1964], with some refinements by Lopez-Escobar [1966] and Dickmann [1975], while (3.4) was proved by Tarski. Result (3.5) is due to Scott [1961], (3.6) to Bell [1970] and [1972]; and (3.7) to Bell [1974]. Measurable cardinals were first considered by Ulam [1930] and Tarski [1939]. The fact that measurable cardinals are weakly compact was noted in Tarski [1962].
§4. The undecidability theorem for
 (ω1,ω1) was proved by
Scott in 1960; a fully detailed proof first appeared in Karp [1964].
The approach to the theorem adopted here is based on the account given
in Dickmann [1975].
(ω1,ω1) was proved by
Scott in 1960; a fully detailed proof first appeared in Karp [1964].
The approach to the theorem adopted here is based on the account given
in Dickmann [1975].
§5. The original motivation for the results presented in this section came from Kreisel; in his [1965] he pointed out that there were no compelling grounds for choosing infinitary formulas solely on the grounds of "length", and proposed instead that definability or "closure" criteria be employed. Kreisel's suggestion was taken up with great success by Barwise [1967], where his compactness theorem was proved. The notion of admissible set is due to Platek [1966]. Theorem (5.6) is taken from Keisler [1974].
For further reading on the subject of infinitary languages, see Aczel [1973], Dickmann [1975], Karp [1964], Keisler [1974], and Makkai [1977].
Bibliography
- Aczel, P., 1973, "Infinitary Logic and the Barwise Compactness Theorem", Proceedings of the 1971 Bertrand Russell Memorial Logic Conference (Uldum, Denmark), J. Bell, J. Cole, G. Priest, and A. Slomson (eds.), Leeds: published by the Bertrand Russell Memorial Logic Conference, 234-277.
- Barwise, J., 1967, Infinitary Logic and Admissible Sets. Ph.D. Thesis, Stanford University.
- Barwise, J., 1973, "Back and Forth through Infinitary Logic. Studies in Model Theory", MAA Studies in Math., Vol. 8, Mat. Assoc. Amer., Buffalo, N.Y., 5-34.
- Bell, J. L., 1970, "Weak Compactness in Restricted Second-Order Languages", Bull. Pol. Acad. Sci. 18: 111-114.
- -----, 1972, "On the Relationship between Weak Compactness in
 (ω1, ω),
(ω1, ω),
 (ω1,
ω1), and Restricted Second-Order Languages",
Arch. Math. Logik 15: 74-78.
(ω1,
ω1), and Restricted Second-Order Languages",
Arch. Math. Logik 15: 74-78. - -----, 1974, "On Compact Cardinals", Z. f. Math. Logik u. Grund. D. Math 20: 389-393.
- -----, 1981, "Isomorphism of Structures in S-toposes", J. Symbolic Logic 43, no. 3, 449-459.
- Chang, C.C., 1968, "Some Remarks on the Model Theory of Infinitary Languages". in The Syntax and Semantics of Infinitary Languages, J. Barwise, ed., Lecture Notes in Mathematics 72, Springer-Verlag, Berlin, 36-63.
- Dickmann, M. A., 1975, Large Infinitary Languages, Amsterdam: North-Holland.
- Ellentuck, E., 1976, "Categoricity Regained", J. Symbolic Logic 41, no. 3, 639-643.
- Hanf, W. P., 1964, Incompactness in Languages with Infinitely Long Expressions, Amsterdam: North-Holland.
- Karp, C., 1964, Languages with Expressions of Infinite Length, Amsterdam: North-Holland.
- -----, 1965, "Finite-Quantifier Equivalence" in The Theory of Models, J. Addison, L. Henkin, and A. Tarski (eds.), Amsterdam: North-Holland, 407-412.
- Keisler, H. J., 1974, Model Theory for Infinitary Logic, Amsterdam: North-Holland.
- Kreisel, G., 1965, "Model-Theoretic Invariants, Applications to Recursive and Hyperarithmetic Operations", in The Theory of Models, J. Addison, L. Henkin, and A. Tarski (eds.), Amsterdam: North-Holland, 190-205.
- Lopez-Escobar, E. G. K., 1965, "An Interpolation Theorem for Infinitely Long Sentences", Fund. Math. 57: 253-272.
- -----, 1966, "On Defining Well-Orderings", Fund. Math. 59: 13-21.
- Makkai, M., 1977, "Admissible Sets and Infinitary Logic", Handbook of Mathematical Logic, J. Barwise (ed.), Amsterdam: North-Holland, 233-282.
- Morley, M., 1965, "Omitting Classes of Elements", The Theory of Models, J. Addison, L. Henkin, and A. Tarski (eds.), Amsterdam: North-Holland, 265-273.
- Platek, R., 1966, Foundations of Recursion Theory, Ph.D. Thesis, Stanford University.
- Scott, D., 1961, "Measurable Cardinals and Constructible Sets", Bull. Acad. Pol. Sci. 9: 521-524.
- -----, 1965, "Logic with Denumerably Long Formulas and Finite Strings of Quantifiers", The Theory of Models, J. Addison, L. Henkin, and A. Tarski (eds.), Amsterdam: North-Holland, 329-341.

