Supplement to Set Theory
Zermelo-Fraenkel Set Theory
Axioms of ZF
Extensionality:This axiom asserts that when sets x and y have the same members, they are the same set.
∀x∀y[∀z(z∈x ≡ z∈y) → x=y]
The next axiom asserts the existence of the empty set:
Null Set:
∃x¬∃y(y ∈ x)
Since it is provable from this axiom and the previous axiom that there is a unique such set, we may introduce the notation ‘Ø’ to denote it.
The next axiom asserts that if given any set x and y, there exists a pair set of x and y, i.e., a set which has only x and y as members:
Pairs:
∀x∀y∃z∀w(w∈z ≡ w=xw=y)
Since it is provable that there is a unique pair set for each given x and y, we introduce the notation ‘{x,y}’ to denote it.
The next axiom asserts that for any given set x, there is a set y which has as members all of the members of all of the members of x:
Unions:
∀x∃y∀z[z∈y ≡ ∃w(w∈x & z∈w)]
Since it is provable that there is a unique ‘union’ of any set x, we introduce the notation ‘∪x’ to denote it.
The next axiom asserts that for any set x, there is a set y which contains as members all those sets whose members are also elements of x, i.e., y contains all of the subsets of x:
Power Set:
∀x∃y∀z[z∈y ≡ ∀w(w∈z → w∈x)]
Since every set provably has a unique ‘power set’, we
introduce the notation
‘
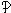(x)’
to denote it. Note also that we may define the notion x is a
subset of y (‘x ⊆ y’) as:
∀
z(z∈x →
z∈y).
Then we may simplify the statement of the Power Set Axiom as
follows:
∀x∃y∀z[z∈y ≡ z⊆x)
The next axiom asserts the existence of an infinite set, i.e., a set with an infinite number of members:
Infinity:
∃x[Ø∈x & ∀y(y∈x → ∪{y,{y}}∈x)]
We may think of this as follows. Let us define the union of x and y (‘x∪y’) as the union of the pair set of x and y, i.e., as ∪{x,y}. Then the Axiom of Infinity asserts that there is a set x which contains Ø as a member and which is such that, anytime y is a member of x, then y∪{y} is a member of x. Consequently, this axiom guarantees the existence of a set of the following form:
{Ø, {Ø}, {Ø, {Ø}}, {Ø, {Ø}, {Ø, {Ø}}}, … }
Notice that the second element, {Ø}, is in this set because (1) the fact that Ø is in the set implies that Ø ∪ {Ø} is in the set and (2) Ø ∪ {Ø} just is {Ø}. Similarly, the third element, {Ø, {Ø}}, is in this set because (1) the fact that {Ø} is in the set implies that {Ø} ∪ {{Ø}} is in the set and (2) {Ø} ∪ {{Ø}} just is {Ø, {Ø}}. And so forth.
The next axiom asserts that every set is ‘well-founded’:
Regularity:
∀x[x≠Ø → ∃y(y∈x & ∀z(z∈x → ¬(z∈y)))]
A member y of a set x with this property is called a ‘minimal’ element. This axiom rules out the existence of circular chains of sets (e.g., such as x∈y & y∈z & and z∈x) as well as infinitely descending chains of sets (such as … x3 ∈ x2 ∈ x1 ∈ x0).
The final axiom of ZF is the Replacement Schema. Suppose that
φ(x,y,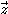
) is a
formula with x and y free, and which may or may not
have free variables
z1,…,zk. Furthermore,
let φx,y,
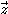[s,r,]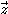
be the result of substituting s and r for
x and y, respectively, in
φ(x,y,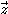). Then
every instance of the following schema is an axiom:
Replacement Schema:
∀z1…∀zk[∀x∃!yφ(x,y,
In other words, if we know that φ is a functional formula (which relates each set x to a unique set y), then if we are given a set u, we can form a new set v as follows: collect all of the sets to which the members of u are uniquely related by φ.
Note that the Replacement Schema can take you ‘out of’ the set
u when forming the set v. The elements of
v need not be elements of u. By contrast,
the well-known Separation Schema of Zermelo yields
new sets consisting only of those elements of a given set u
which satisfy a certain condition
ψ. That is, suppose that
ψ(x,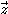) has
x free and may or may not have
z1,…,zk free.
Then the Separation Schema asserts:
Separation Schema ∀z1…∀zk[∀u∃v∀r(r∈v ≡ r∈u & ψx,
In other words, if given a formula ψ and a set u, there exists a set v which has as members precisely the members of u which satisfy the formula ψ.