Stanford Encyclopedia of Philosophy

Supplement to Common Knowledge

Proof of Proposition 2.17

Proposition 2.17 (Aumann 1976)
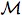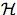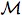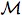Let calligraphic-M be the meet of the agents' partitions calligraphic-Hi for each i ∈ N. A proposition E ⊆ Ω is common knowledge for the agents of N at ω iff calligraphic-M(ω) ⊆ E. In Aumann (1976), E is defined to be common knowledge at ω iff calligraphic-M(ω) ⊆ E.

Proof.
(⇐) By Lemma 2.16, 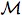calligraphic-M( ω ) is common knowledge at ω, so E is common knowledge at ω by Proposition 2.4.

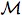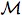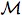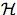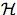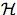(⇒) We must show that K*N(E) implies that calligraphic-M(ω) ⊆ E. Suppose that there exists ω′ ∈ calligraphic-M(ω) such that ω′ ∉ E. Since ω′ ∈ calligraphic-M(ω), ω′ is reachable from ω, so there exists a sequence 0, 1, … , m−1 with associated states ω1, ω2, … , ωm and information sets calligraphic-Hik(ωk) such that ω0 = ω, ωm = ω′, and ωk ∈ calligraphic-Hik(ωk+1). But at information set calligraphic-Hik(ωm), agent ik does not know event E. Working backwards on k, we see that event E cannot be common knowledge, that is, agent i1 cannot rule out the possibility that agent i2 thinks that … that agent im−1 thinks that agent im does not know E. □

Return to Common Knowledge