Notes to Many-Worlds Interpretation of Quantum Mechanics
1. The mathematical part of the MWI, (i), yields less than mathematical parts of some other theories such as, e.g., Bohmian mechanics. Indeed, our experience is consistent with the MWI, but it does not follow from its mathematical part. The Schrödinger equation itself does not explain why we experience definite results in quantum measurements. In contrast, in the Bohmian mechanics the mathematical part yields almost everything, and the analog of (ii) is very simple: it is the postulate according to which only the "Bohmian positions" (and not the quantum wave) correspond to our experience. The Bohmian positions of all particles yield the familiar picture of the (single) world we are aware of. Thus, philosophically, a theory like the Bohmian mechanics achieves more than the MWI, but at the price of a significant impairment of the physical aspects of the theory, e.g., addition of the non-local dynamics of Bohmian particle positions. However, Wallace (2001a) argues that stripping the experiential content from empty waves in the Bohmian approach has significant philosophical difficulties too.
2. Wallace 2001a points out that the term “superposition of a cat” is a misnomer. I use it as a shortcut for “a superposition of states of elementary particles corresponding to different (classical) states of the cat”.
3. It corresponds to the fact that we are aware of objects like cats, tables, etc. that are well localized and are in a definite state. The position need not and must not be exact: its uncertainty should be small only relative to the precision with which we can measure it and the uncertainty must remain such for a period of time. Therefore, due to the uncertainty principle, it cannot be too small.
4. The quantum state of the
world is the normalized projection of the quantum state of the
Universe onto the space corresponding to the classical description of
the world. It is a product state only for variables which are
relevant for the macroscopic description of the objects. There might
be some entanglement between weakly coupled variables like nuclear
spins belonging to different objects. In order to keep the form of
the quantum state of the world (1), the quantum state of such
variables should belong to
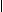 Φ
Φ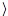 .
.
5. Since there is a strong philosophical denial of a possibility to have a nondichotomic degree of existence, the name is clearly problematic, however, it seems that no other word fits better.
6. An even more severe difficulty of this kind appears in the consistent-histories approach considered by Gell-Mann and Hartle as an advanced MWI. Its basic concept, the probability of a history, seems to be meaningless since all histories exist. However, Saunders finds this approach useful for the analysis of probability.
7. This postulate is a counterpart of the collapse postulate of standard quantum mechanics according to which, after measurement, the quantum state collapses to a particular branch with probability proportional to its squared amplitude. (See the entry on quantum mechanics.) However, it differs in two aspects. First, it is the parallel of only the second part of the collapse postulate, the Born Rule, and second, it is related only to part (ii) of the MWI, the connection to our experience, and not to the mathematical part of the theory (i).
8. Proponents of the MWI might argue that, in fact, the burden of an experimental proof lies on the opponents of the MWI, because it is they who claim that there is new physics beyond the well tested Schrödinger equation.
9. Steane challenges the claim that a quantum computer performs parallel computations, but this is certainly the most natural interpretation of the operation of the first quantum algorithm which works faster than any classical one, see Experiment 2 in Deutsch (1986).

