Two Counter-Models Regarding Additions to SDL

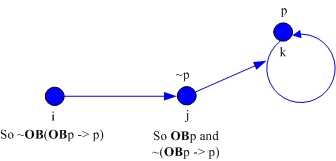
We now provide a counter-model to show that A4, OB(OBp → p), is indeed a genuine (non-derivable) addition to SDL:

Here, seriality holds, since each of the three worlds has at least one world acceptable to it (in fact, exactly one), but secondary seriality fails, since although j is acceptable to i, j is not acceptable to itself. Now look at the top annotations regarding the assignment of truth or falsity to p at j and k. The lower deontic formuli derive from this assignment and the accessibility relations. (The value of p at i won't matter.) Since p holds at k, which exhausts the worlds acceptable to j, OBp must hold at j, but then, since p itself is false at j, (OBp → p) must be false at j. But j is acceptable to i, so not all i-acceptable worlds are ones where (OBp → p) holds, so OB(OBp → p) must be false at i.^[1] We have already proven that seriality, which holds in this model, automatically validates OB-D. It is easy to show that the remaining ingredients of SDL hold here as well.^[2]

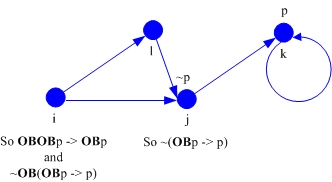
We proved above that (OBOBp → OBp) is derivable from A4. Here is a model that shows that the converse fails. It is left to the reader to verify that given the accessibility relations and indicated assignments to p at j and k, OBOBp → OBp must be (vacuously) true at i, while OB(OBp → p) must be false at i.

Return to Deontic Logic.