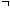
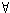 x
x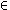
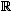 (P(x)
(P(x) 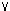
 P(x))
P(x))| This is a file in the archives of the Stanford Encyclopedia of Philosophy. |
Here is the argument for Brouwer's strong counterexample to one form of PEM that he mentions in his paper from 1928, ‘Betrachtungen über den Formalismus’ (‘Reflections on Formalism’). We will show that
where P(x) = ‘x is rational’ andx
(P(x)
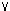
P(x))
 is the intuitionistic
continuum. Accordingly, in this context
real numbers are to be understood
intuitionistically (namely, as convergent choice sequences).
is the intuitionistic
continuum. Accordingly, in this context
real numbers are to be understood
intuitionistically (namely, as convergent choice sequences).
We first show that the continuum cannot be split, that is, there are
no non-empty spreads A and B such that A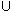 B =
B =
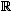 and A
and A B =
B =
 .
For assume there are;
then the function f:
.
For assume there are;
then the function f: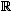
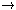
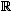 defined by
defined by
is total and therefore, by Brouwer's continuity theorem (generalized from [0,1] to
f(x) = {
0 if x A
1 if x B
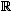 ),
continuous.
But then f must be constant, so either A or B is equal
to
),
continuous.
But then f must be constant, so either A or B is equal
to
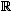 , and the other
spread must be empty. This however contradicts the assumption that both
A and B are non-empty.
, and the other
spread must be empty. This however contradicts the assumption that both
A and B are non-empty.
From the non-splittability of the continuum it follows that
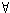 x
x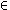
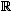 (P(x)
(P(x) 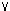
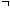 P(x))
is false.
For if it were true, we could obtain a splitting of the continuum by
letting f assign 0 to the rational real numbers (A), and 1 to the
irrational ones (B); but this is impossible, as just shown. Hence,
P(x))
is false.
For if it were true, we could obtain a splitting of the continuum by
letting f assign 0 to the rational real numbers (A), and 1 to the
irrational ones (B); but this is impossible, as just shown. Hence,
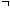
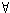 x
x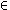
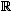 (P(x)
(P(x) 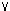
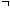 P(x)).
P(x)).
Brouwer established non-splittability of
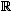 in 1927, in footnote 10
of ‘Definitionsbereiche von Funktionen’
(‘On the Domains
of Definition of Functions’).
in 1927, in footnote 10
of ‘Definitionsbereiche von Funktionen’
(‘On the Domains
of Definition of Functions’).
Other strong counterexamples that Brouwer devised are
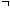
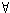 x
x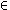
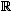 (
(
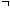 x < 0
x < 0
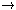 x < 0)
(Brouwer, 1949a)
x < 0)
(Brouwer, 1949a)
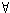 x
x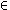
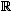 (x
(x 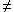 0
0 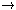 x < 0
x < 0 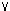 x > 0)
(Brouwer, 1949b)
x > 0)
(Brouwer, 1949b)| Mark van Atten Mark.vanAtten@univ-paris1.fr |