Optimality-Theoretic and Game-Theoretic Approaches to Implicature
Linguistic pragmatics studies the interpretation of expressions in the particular contexts in which they are used. Perhaps the most important notion in pragmatics is Grice's (1967) notion of conversational implicature. It is based on the insight that by means of general principles of rational cooperative behavior we can communicate more with the use of a sentence than the conventional semantic meaning associated with it. Grice has argued, for instance, that the exclusive interpretation of ‘or’ — according to which we infer from ‘John or Mary came’ that John and Mary didn't come both — is not due to the semantic meaning of ‘or’ but should be accounted for by a theory of conversational implicatures. In this particular example, — a typical example of a so-called Quantity implicature — the hearer's implication is taken to follow from the fact that the speaker could have used a contrasting, and informatively stronger expression, but chose not to. Grice suggested that other implicatures follow from what the hearer thinks that the speaker takes to be the normal state of affairs. For both types of implicatures, the hearer's (pragmatic) interpretation of an expression involves what he takes to be the speaker's reason for using this expression. But obviously, this speaker's reason must involve assumptions about the hearer's reasoning as well.
In this entry we will discuss two ‘theories’ of conversational implicatures that explicitly take the interactive reasoning of speaker and hearer into account: (Bidirectional) Optimality Theory and Game Theory.
- 1. Bidirectional Optimality Theory
- 2. Implicatures and Game Theory
- 3. Conclusion
- Bibliography
- Other Internet Resources
- Related Entries
1. Bidirectional Optimality Theory
1.1 Bidirectional OT and Quantity implicatures
Optimality Theory (OT) is a linguistic theory which assumes that linguistic choices are governed by competition between a set of candidates, or alternatives. In standard OT (Prince & Smolensky, 1993) the optimal candidate is the one that satisfies best a set of violable constraints. After its success in phonology, OT has been used also in the theory of meaning. The original idea here was to take the candidates to be the alternative interpretations that the hearer could assign to the given expression. Blutner (1998, 2000) extended this original version by taking also alternative expressions, or forms, into account that the speaker could have used, but did not. The reference to alternative expressions/forms is standard in pragmatics to account for Quantity implicatures. Optimization should thus be thought of from two directions: that of the hearer, and that of the speaker. What is optimal, according to Blutner's Bidirectional-OT (Bi-OT), is not just interpretations with respect to forms, but rather form-interpretation pairs. In terms of a ‘better than’ relation ‘>’ between form-interpretation pairs, the pair ⟨f,i⟩ is said to be (strongly) optimal iff it satisfies the following two conditions:
- ¬∃i′ : ⟨f,i′⟩ > ⟨f,i⟩
- ¬∃f′ : ⟨f′,i⟩ > ⟨f,i⟩
The first condition requires that i is an optimal interpretation of
form f. In Bi-OT this condition is thought of as optimization from
the hearer's point of view. Blutner proposes that
⟨f,i′⟩ >
⟨f,i⟩
iff i′ is a more likely, or stereotypical, interpretation of
f than i is:
P(i′ | 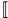 f
f ![]]](rsem.jpg) )
>
P(i |
)
>
P(i | 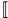 f
f ![]]](rsem.jpg) )
(where
)
(where
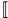 f
f ![]]](rsem.jpg) denotes the semantic meaning of f, and
P(B | A) the conditional
probability of B given A, defined as
P(A∩B)/P(A)). The
second condition is taken to involve speaker's optimization:
for
⟨f,i⟩
to be optimal for the speaker, it has to be the case that she cannot
use a more optimal form f ′ to express
i.
⟨f ′,i⟩
>
⟨f,i⟩
iff either (i)
P(i |
denotes the semantic meaning of f, and
P(B | A) the conditional
probability of B given A, defined as
P(A∩B)/P(A)). The
second condition is taken to involve speaker's optimization:
for
⟨f,i⟩
to be optimal for the speaker, it has to be the case that she cannot
use a more optimal form f ′ to express
i.
⟨f ′,i⟩
>
⟨f,i⟩
iff either (i)
P(i | 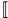 f ′
f ′![]]](rsem.jpg) )
>
P(i |
)
>
P(i | 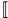 f
f ![]]](rsem.jpg) ),
or (ii)
P(i |
),
or (ii)
P(i | 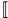 f ′
f ′![]]](rsem.jpg) )
=
P(i |
)
=
P(i | 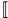 f
f ![]]](rsem.jpg) )
and f ′ is a less complex form to express
i than f is.
)
and f ′ is a less complex form to express
i than f is.
Blutner's bidirectional OT accounts for classical Quantity implicatures. An example of such an (assumed) Quantity implicatures is the ‘exactly’-interpretation of number terms. Let us assume, with other Griceans, that number-terms semantically have an ‘at least’ meaning.[1] Still, we want to account for the intuition that the sentence “Three children came to the party” is normally interpreted as saying that Exactly three children came to the party. One way to do this is to assume that the alternative expressions that the speaker could use are of the form “(At least) n children came to the party”, while the alternative interpretations for the hearer are of type in meaning that “Exactly n children came to the party”.[2] If we then assume that the probabilities are equally distributed over the interpretations and that it is already commonly assumed that some children came, but not more than four, a bidirectional formalization gives rise to the following table, with the desired outcome.
P(i | f
)
i1 i2 i3 i4 ‘one’ ⇒¼ ¼ ¼ ¼ ‘two’ 0 ⇒1⁄3 1⁄3 1⁄3 ‘three’ 0 0 ⇒½ ½ ‘four’ 0 0 0 ⇒1
In this table the entry
P(i3 | 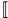 ‘two’
‘two’![]]](rsem.jpg) ) =
1⁄3 because
P(i3 | {i2,i3,i4})
= 1⁄3. Notice that according to this
reasoning ‘two’ is interpreted as ‘exactly 2’
(as indicated by an arrow) because (i)
P(i2 |
) =
1⁄3 because
P(i3 | {i2,i3,i4})
= 1⁄3. Notice that according to this
reasoning ‘two’ is interpreted as ‘exactly 2’
(as indicated by an arrow) because (i)
P(i2 | 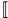 ‘two’
‘two’![]]](rsem.jpg) )
= 1⁄3 is higher than
P(i2 |
)
= 1⁄3 is higher than
P(i2 | 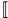 ‘n’
‘n’![]]](rsem.jpg) )
for any alternative expression ‘n’, and (ii) all
other interpretations compatible with the semantic meaning of the
numeral expression are blocked: there is, for instance,
another expression for which i4 is a better
interpretation, i.e., an interpretation with a higher conditional
probability.
)
for any alternative expression ‘n’, and (ii) all
other interpretations compatible with the semantic meaning of the
numeral expression are blocked: there is, for instance,
another expression for which i4 is a better
interpretation, i.e., an interpretation with a higher conditional
probability.
With numeral terms, the semantic meanings of the alternative expressions give rise to a linear order. This turns out to be crucial for the Bi-OT analysis, if we continue to take the interpretations as specific as we have done so far. Consider the following alternative answers to the question “Who came to the party?”:
- John came to the party.
- John or Bill came to the party.
Suppose that John and Bill are the only relevant persons and that it is presupposed that somebody came to the party. In that case the bidirectional table looks as follows (where ix is the interpretation that only x came):
P(i | f
)
ij ib ijb ‘John’ ⇒½ 0 ½ ‘Bill’ 0 ⇒½ ½ ‘John and Bill’ 0 0 ⇒ 1 ‘John or Bill’ 1⁄3 1⁄3 1⁄3
This table correctly predicts that (1) is interpreted as saying that only John came. But now consider the disjunction (2). Intuitively, this answer should be interpreted as saying that either only John, or only Bill came: the scalar implicature. It is easy to see, however, that this is predicted only if ‘John came’ and ‘Bill came’ are not taken to be alternative forms. Bi-OT predicts that in case also ‘John came’ and ‘Bill came’ are taken to be alternatives, the disjunction is uninterpretable, because the specific interpretations ij, ib, and ijb all can be expressed better by other forms. In general, one can see that in case the semantic meanings of the alternative expressions are not linearly, but only partially ordered, the derivation of Quantity implicatures sketched above gives rise to partially wrong predictions.
As it turns out, this problem for Bi-OT seems larger than it really is. Intuitively, an answer like (2) expresses incomplete information, and to take this into account in Bi-OT (or in any other analysis of Quantity implicatures) we should allow for alternative interpretations in the table that have partial information. It can be shown that if we take the alternative interpretations to be such partial information states, what Bi-OT ends up with is the pragmatic interpretation function called ‘Grice’ in various (joint) papers of Schulz and Van Rooij (e.g. Schulz & Van Rooij, 2006). In these papers it is claimed that Grice implements the Gricean maxim of Quality and the first maxim of Quantity, and it is shown that in terms of it (together with an additional assumption of competence) we can account for many conversational implicatures, including the ones of (1) and (2).
1.2 A Bi-OT analysis of Horn's division
Bi-OT can also account for Horn's division of pragmatic labor — according to which an (un)marked expression (morphologically complex and less lexicalized) typically gets an (un)marked interpretation — which Horn (1984) claimed to follow from the interaction between both Gricean submaxims of Quantity, and the maxims of Relation and Manner. To illustrate, consider the following well-known example:
- John killed the sheriff.
- John caused the sheriff to die.
We typically interpret the unmarked (3) as meaning stereotypical killing (on purpose), while the marked (4) suggests that John killed the sheriff in a more indirect way, and unintentionally. Blutner (1998, 2000) shows that this can be accounted for in his Bidirectional OT. Take ist to be the more plausible interpretation where John killed the sheriff in the stereotypical way, while i¬st is the interpretation where John caused the sheriff's death in an unusual way. Because (3) is less complex than (4), and ist is the more stereotypical interpretation compatible with the semantic meaning of (3), it is predicted that (3) is interpreted as ist. Thus, in terms of his notion of strong optimality, meaning that ⟨f,i⟩ is optimal both for the speaker and the hearer, Blutner can account for the intuition that sentences typically get the most plausible, or stereotypical, interpretation. In terms of this notion of optimality, however, Blutner is not able yet to explain how the more complex form (4) can have an interpretation at all, in particular, why it will be interpreted as non-stereotypical killing. The reason is that on the assumption that (4) has the same semantic meaning as (3), the stereotypical interpretation would be hearer-optimal not only for (3), but also for (4). This interpretation of (4) is blocked, however, by the cheaper alternative expression (3). To account for the intuition that (4) is interpreted in a non-stereotypical way, Blutner (2000) introduces a weaker notion of optimality. In our setup we can say that a form-interpretation pair ⟨f,i⟩ is weakly optimal[3] iff there is neither a strongly optimal ⟨f,i′⟩ such that ⟨f,i′⟩ > ⟨f,i⟩ nor a strongly optimal ⟨f ′,i⟩ such that ⟨f ′,i⟩ > ⟨f,i⟩. All form-interpretation pairs that are strongly optimal are also weakly optimal. However, a pair that is not strongly optimal like ⟨(4),ist⟩ can still be weakly optimal: because neither ⟨(4),ist⟩ nor ⟨(3),i¬st⟩ is strongly optimal, there is no objection for ⟨(4),i¬st⟩ to be a (weakly) optimal pair. As a result, the marked (4) will get the non-stereotypical interpretation.
2. Implicatures and Game Theory
2.1 Signaling games
David Lewis (1969) introduced signaling games to explain how messages can be used to communicate something, although these messages do not have a pre-existing meaning. In pragmatics we want to do something similar: explain what is actually communicated by an expression which actual interpretation is underspecified by its conventional semantic meaning. It is therefore a natural idea to base pragmatics on Lewisian signaling games.
A signaling game is a game of asymmetric information between a sender
s and a receiver r. The sender observes the state
t that s and r are in, while the receiver
has to perform an action. Sender s can try to influence the
action taken by r by sending a message. T is the
set of states, F the set of forms, or messages. We assume
that the messages already have a semantic meaning, given by the
semantic interpretation function
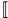 ·
·![]]](rsem.jpg) which assigns to each form a subset of T. The sender will
send a message/form in each state, a sender strategy S is
thus a function from T to F. We assume that the
speaker has to say something that (semantically) is true. The receiver
will perform an action after hearing a message with a particular
semantic meaning, but for present purposes we can think of actions
simply as interpretations. Thus, a receiver strategy R is a
function taking a message into an interpretation, i.e., a subset of
T. We assume that the utility functions of s and
r (Us and Ur) are the
same (implementing Grice's cooperation principle), and that they
depend on (i) the state, t that s and r are
in, (ii) the receiver's interpretation, i, of the message
f sent by s in t according to their
respective strategies R and S, i.e., i =
R(S(t)), and (iii) (in section 3.3) the
message being sent in t by the sender, f =
S(t). We assume that Nature picks the state
according to some (commonly known) probability distribution P
over T. With respect to this probability function, we can
determine the expected, or average, utility of each sender-receiver
strategy combination
⟨S,R⟩
for player e ∈ {s,r} as follows:
which assigns to each form a subset of T. The sender will
send a message/form in each state, a sender strategy S is
thus a function from T to F. We assume that the
speaker has to say something that (semantically) is true. The receiver
will perform an action after hearing a message with a particular
semantic meaning, but for present purposes we can think of actions
simply as interpretations. Thus, a receiver strategy R is a
function taking a message into an interpretation, i.e., a subset of
T. We assume that the utility functions of s and
r (Us and Ur) are the
same (implementing Grice's cooperation principle), and that they
depend on (i) the state, t that s and r are
in, (ii) the receiver's interpretation, i, of the message
f sent by s in t according to their
respective strategies R and S, i.e., i =
R(S(t)), and (iii) (in section 3.3) the
message being sent in t by the sender, f =
S(t). We assume that Nature picks the state
according to some (commonly known) probability distribution P
over T. With respect to this probability function, we can
determine the expected, or average, utility of each sender-receiver
strategy combination
⟨S,R⟩
for player e ∈ {s,r} as follows:
EUe(S,R) = ∑t∈T P(t) × Ue(t,S(t),R(S(t))).
A solution of the game is called a Nash Equilibrium. A Nash Equilibrium of a signaling game is a pair of strategies ⟨S*,R*⟩ which has the property that neither the sender nor the receiver could increase his or her expected utility by unilateral deviation. Thus, S* is a best response to R* and R* is a best response to S*.
2.2 Games and Quantity implicatures
To illustrate the game theoretical treatment of Quantity implicatures, we
willl look for simplicity at numerical expressions
again.[4] Take
a signaling game with 3 states, T =
{t1,t2,t3},
and three messages F =
{‘one’,‘two’,‘three’}. On a
neo-Gricean ‘at least’-interpretation of numerals, the
meanings of the numeral expressions form an implication chain:
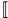 ‘three’
‘three’![]]](rsem.jpg) ⊂
⊂
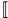 ‘two’
‘two’![]]](rsem.jpg) ⊂
⊂
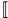 ‘one’
‘one’![]]](rsem.jpg) .
The speaker has to say something that is true. Thus, if the speaker
is in t3 — the situation that three men came
to the party — she could send all three messages, but if she is
in a situation where only one man came, t1, she
could say only that. This means that the speaker can choose between 6
different strategies:
.
The speaker has to say something that is true. Thus, if the speaker
is in t3 — the situation that three men came
to the party — she could send all three messages, but if she is
in a situation where only one man came, t1, she
could say only that. This means that the speaker can choose between 6
different strategies:
S1 = {⟨t1,‘one’⟩, ⟨t2,‘one’⟩, ⟨t3,‘one’⟩} S2 = {⟨t1,‘one’⟩, ⟨t2,‘one’⟩, ⟨t3,‘two’⟩} S3 = {⟨t1,‘one’⟩, ⟨t2,‘one’⟩, ⟨t3,‘three’⟩} S4 = {⟨t1,‘one’⟩, ⟨t2,‘two’⟩, ⟨t3,‘one’⟩} S5 = {⟨t1,‘one’⟩, ⟨t2,‘two’⟩, ⟨t3,‘two’⟩} S6 = {⟨t1,‘one’⟩, ⟨t2,‘two’⟩, ⟨t3,‘three’⟩}
The receiver's action is one of interpretation: he will assign an
interpretation to each message. We assume that for each message
f and receiver strategy R, R(f)
⊆
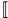 f
f ![]]](rsem.jpg) .
This means that the receiver can choose between 6 strategies:
.
This means that the receiver can choose between 6 strategies:
R1 = {⟨‘one’,{t1}⟩, ⟨‘two’,{t2}⟩, ⟨‘three’,{t3}⟩} R2 = {⟨‘one’,{t1}⟩, ⟨‘two’,{t2,t3}⟩, ⟨‘three’,{t3}⟩} R3 = {⟨‘one’,{t1,t2}⟩, ⟨‘two’,{t2}⟩, ⟨‘three’,{t3}⟩} R4 = {⟨‘one’,{t1,t2}⟩, ⟨‘two’,{t2,t3}⟩, ⟨‘three’,{t3}⟩} R5 = {⟨‘one’,{t1,t2,t3}⟩, ⟨‘two’,{t2}⟩, ⟨‘three’,{t3}⟩} R6 = ·
=
{⟨‘one’,{t1,t2,t3}⟩, ⟨‘two’,{t2,t3}⟩, ⟨‘three’,{t3}⟩}
We assume that the message being sent is costless, and that the utility function is similar to the conditional probability function that ordered the interpretations in our description of Bi-OT: Us(t,R(f)) = Ur(t,R(f)) = P(t | R(f)) = 1/|R(f)| if t ∈ R(f), 0 otherwise (where |X| denotes the cardinality of set X). Now we can determine for each sender-receiver strategy combination its expected utility:
EU(S,R) R1 R2 R3 R4 R5 R6 S1 1⁄3 1⁄3 1⁄3 1⁄3 1⁄3 1⁄3 S2 1⁄3 ½ 1⁄3 ½ 2⁄9 7⁄18 S3 2⁄3 2⁄3 7⁄12 7⁄12 5⁄9 5⁄9 S4 2⁄3 4⁄9 ½ 1⁄3 5⁄9 5⁄18 S5 2⁄3 ½ ½ 1⁄3 4⁄9 5⁄18 S6 ⇒1 5⁄6 5⁄6 4⁄6 7⁄9 11⁄18
From this table we can easily see that the pair ⟨S6,R1⟩ is the only Nash equilibrium of this game. This is so because for all other combinations ⟨S,R⟩, both players could always benefit if one of them would choose another strategy. Notice that our unique Nash equilbrium gives rise to a set of form-interpretation pairs that is exactly the set of bidirectionally optimal form-interpretation pairs as described in the previous section according to which the number terms are given an ‘exactly’-interpretation, which is the standard Quantity implicature.
Just as for the case of Bi-OT, our game-theoretical account of Quantity implicatures is both not general enough and too specific. It is not general enough, because we don't want to limit ourselves to classical scalar implicatures, where the semantic meanings of the alternative expressions form an implicational chain. It is too specific, because we don't want to assume that the speaker has complete information and knows in which state she is. Moreover, we haven't met Grice's explicit demand to take the purpose of the conversation into account. Fortunately, just as Bi-OT can do better, the game-theoretical analysis can be extended to overcome these limitations as well. It would be beyond the scope of this entry to describe these extensions, though.
2.3 A game theoretical explanation of Horn's division
So far we have assumed that messages are costless: the utility function does not depend on the message being sent, but only on the state s and r are in, and the action/interpretation chosen by r. Parikh (1991, 2001) shows that if we also make use of costly messages, we can account for Horn's division of pragmatic labor.
Suppose we have 2 states, tst and t¬st, and 2 messages, fu and fm. Assume that the semantic meaning of both messages is {tst,t¬st}, but that tst is more stereotypical, or probable, than t¬st: P(tst) > P(t¬st). The sender's utility function will be decomposable into a benefit and a cost function, Us(t,f,i) = Bs(t,i) − C(f), where i is an interpretation. We adopt the following benefit function: Bs(t,i) = 1 if i = t, and Bs(t,i) = 0 otherwise. The cost of the unmarked message fu is lower than the cost of the marked message fm. We can assume without loss of generality that C(fu) = 0 < C(fm). We also assume that it is always better to have successful communication with a costly message than unsuccessful communication with a cheap message, which means that C(fm), though greater than C(fu), must remain reasonable small. The sender and receiver strategies are as before. The combination of sender and receiver strategies that gives rise to the bijective mapping {⟨tst,fu⟩, ⟨t¬st,fm⟩} is a Nash equilibrium of this game. And this equililbrium encodes Horn's division of pragmatic labor: the unmarked (and lighter) message fu expresses the stereotypical interpretation tst, while the non-stereotypical state t¬st is expressed by the marked and costlier message fm. Unfortunately, also the mapping {⟨tst,fm⟩, ⟨t¬st,fu⟩} — where the lighter message denotes the non-stereotypical situation — is a Nash equilibrium of the game, which means that on the present implementation the standard solution concept of game theory cannot yet single out the desired outcome.
Parikh (1991, 2001) argues that to account for this problem we should adopt another, and more fine-grained, solution concept. He observes that of the two equilibria mentioned above, the first one Pareto-dominates the second, and that for this reason the former should be preferred. Van Rooij (2004) suggests that because Horn's division of pragmatic labor involves not only language use but also language organization, one should look at signaling games from an evolutionary point of view, and make use of those variants of evolutionary game theory that explain the emergence of Pareto-optimal solutions.
Conclusion
Bidirectional Optimality Theory and Game Theory are quite natural, and similar, frameworks to account for some basic conversational implicatures. It was noted that straightforward applications of these frameworks are sometimes not general enough and may depend on unnatural assumptions, but that these limitations can be overcome by making appropriate generalizations.
The examples discussed above were limited, but central. Other implicatures not discussed at all here involve truthfulness, politeness, and manner of speech. Game Theoretical accounts of such implicatures have been proposed as well, but it would be beyond the scope of this entry to go into any of these proposals.
Bibliography
- Blutner, R. (1998), ‘Lexical Pragmatics’, Journal of Semantics, 15: 115-162.
- Blutner, R. (2000), ‘Some aspects of optimality in natural language interpretation’, Journal of Semantics, 17: 189-216.
- Gazdar, G. (1979), Pragmatics, Academic Press, London.
- Grice, H.P. (1967), ‘Logic and conversation’, William James Lectures, Harvard University, reprinted in Studies in the Way of Words, 1989, Harvard University Press, Cambridge, Massachusetts.
- Horn, L. (1984), ‘Towards a new taxonomy of pragmatic inference: Q-based and R-based implicature’. In: D. Schiffrin (ed.), Meaning, Form, and Use in Context: Linguistic Applications, GURT84, 11-42, Washington; Georgetown University Press.
- Jäger, G. (2006), Game dynamics connects semantics and pragmatics, ms. University of Bielefeld.
- Lewis, D. (1969), Convention, Cambridge: Harvard University Press.
- Parikh, P. (1991), ‘Communication and strategic inference’, Linguistics and Philosophy, 14: 473-513.
- Parikh, P. (2001), The use of Language, CSLI Publications, Stanford, California.
- Prince, A. and P. Smolensky, (1993), Optimality Theory. Constraint interaction in generative grammar, MIT Press, Cambridge, Mass.
- Rooij, R. van (2004), ‘Relevance and Bidirectional OT’, In: R. Blutner and H. Zeevat (eds.), Optimality Theory and Pragmatics, Palgrave Macmillan, 2004, pp. 173-210.
- Rooij, R. van (2004), ‘Signalling games select Horn strategies’, Linguistics and Philosophy, 27: 493-527.
- Schulz, K., and R. van Rooij (2006), ‘Pragmatic meaning and non-monotonic reasoning: the case of exhaustive interpretation’, Linguistics and Philosophy, 29: 205-250.
Other Internet Resources
[Please contact the author with suggestions.]
Related Entries
defaults in semantics and pragmatics | game theory | Grice, Paul | implicature

