Supertasks
Supertasks have posed problems for philosophy since the time of Zeno of Elea. The term ‘supertask’ is new but it designates an idea already present in the formulation of the old motion paradoxes of Zeno, namely the idea of an infinite number of actions performed in a finite amount of time. The main problem lies in deciding what follows from the performance of a supertask. Some philosophers have claimed that what follows is a contradiction and that supertasks are, therefore, logically impossible. Others have denied this conclusion, and hold that the study of supertasks can help us improve our understanding of the physical world, or even our theories about it.
- 1. What is a Supertask
- 2. On The Conceptual Possibility Of Supertasks
- 3. On The Physical Possibility Of Supertasks
- 4. The Physics of Supertasks
- 4.1 A New Form of Indeterminism: Spontaneous Self-Excitation
- 4.2 A New Form of Indeterminism: Global Interaction
- 4.3 Energy and Momentum Conservation in Supertasks
- 4.4 Actions without Interaction
- 4.5 The Spaceship Paradox
- 4.6 Bifurcated Supertasks
- 4.7 Bifurcated Supertasks and the Solution to the Philosophical Problem of Supertasks
- 5. What Supertasks Entail for the Philosophy of Mathematics
- Bibliography
- Other Internet Resources
- Related Entries
1. What is a Supertask
1.1 Definitions
A supertask may be defined as an infinite sequence of actions or operations carried out in a finite interval of time. The terms ‘action’ and ‘operation’ must not be understood in their usual sense, which involves a human agent. Human agency may be involved but it is not necessary. To show this, let us see how actions can be characterised precisely without any references to man. We will assume that at each instant of time the state of the world relevant to a specific action can be described by a set S of sentences. Now an action or operation applied to a state of the world results in a change in that state, that is, in the set S corresponding to it. Consequently, an arbitrary action a will be defined (Allis and Koetsier 1995) as a change in the state of the world by which the latter changes from state S before the change to state a(S) after it. This means that an action has a beginning and an end, but does not entail that there is a finite lapse of time between them. For instance, take the case of a lamp that is on at t = 0 and remains so until t = 1, an instant at which it suddenly goes off. Before t =1 the state of the lamp (which is the only relevant portion of the world here) can be described by the sentence ‘lamp on’, and after t =1 by the sentence ‘lamp off’, without there being a finite lapse of time between the beginning and the end of the action. Some authors have objected to this consequence of the definition of action, and they might be right if we were dealing with the general philosophical problem of change. But we need not be concerned with those objections at this stage, since in the greatest majority of the relevant supertasks instantaneous actions (i.e., actions without any duration) can be replaced by actions lasting a finite amount of time without affecting the analysis at any fundamental point.
There is a particular type of supertask called hypertasks. A hypertask is a non-numerable infinite sequence of actions or operations carried out in a finite interval of time. Therefore, a supertask which is not a hypertask will be a numerable infinite sequence of actions or operations carried out in a finite interval of time. Finally, a task can be defined as a finite sequence of actions or operations carried out in a finite interval of time.
1.2 The Philosophical Problem of Supertasks
To gain a better insight into the fundamental nature of the philosophical problem posed by supertasks, consider the distinction between tasks in general (finite sequences of actions of the type (a1, a2, a3, … , an)) and one particular type of supertasks, namely those consisting of an infinite sequence of actions of the type (a1, a2, a3, … , an, … ) and thus having the same type of order as the natural order of positive integers: 1, 2, 3, … , n, … (it is customary to denote this type of order with letter ‘w’ and so the related supertasks can be called supertasks of type w).
In the case of a task T = (a1, a2, a3, … , an) it is natural to say that T is applicable in state S if:
a1 is applicable to S,
a2 is applicable to a1(S),
a3 is applicable to a2(a1(S)),
… , and,
an is applicable to an−1(an−2(… (a2(a1(S)))… )).
The successive states of the world relevant to task T can be defined by means of the finite sequence of sets of sentences:
S, a1(S), a2(a1(S)), a3(a2(a1(S))), …, an(an−1(an−2 (… (a2(a1(S)))…))),
whose last term will therefore describe the relevant state of the world after the performance of T. Or, equivalently, the state resulting from applying T to S will be T(S) =
an(an−1(an−2 (… (a2(a1(S)))… ))).
Now take the case of a supertask T = (a1, a2, a3, …, an, …). Let us give the name Tn to the task which consists in performing the first n actions of T. That is, Tn = (a1, a2, a3, …, an). Now it is natural to say that T is applicable in state S if Tn is applicable in S for each natural number n, and, obviously,
Tn(S) = an(an−1(an−2 (…(a2(a1(S)))…))).
The successive states of the world relevant to supertask T can be described by means of the infinite sequence of sets of sentences:
S, T1(S), T2(S), …, Tn(S), …
A difficulty arises, however, when we want to specify the set of sentences which describe the relevant state of the world after the performance of supertask T, because the infinite sequence above lacks a final term. Put equivalently, it is difficult to specify the relevant state of the world resulting from the application of supertask T to S because there seems to be no final state resulting from such an application. This inherent difficulty is increased by the fact that, by definition, supertask T is performed in a finite time, and so there must exist one first instant of time t* at which it can be said that the performance happened. Now notice that the world must naturally be in a certain specific state at t*, which is the state resulting from the application of T, but that, nevertheless, we have serious trouble to specify this state, as we have just seen.
1.3 Supertask: A Fuzzy Concept
Since we have defined supertasks in terms of actions and actions in terms of changes in the state of the world, there is a basic indeterminacy regarding what type of processes taking place in time should be considered supertasks, which is linked to the basic indeterminacy that there is regarding which type of sets of sentences are to be allowed in descriptions of the state of the world and which are not. For this reason, there are some processes that would be regarded as supertasks by virtually every philosopher and some about which opinions differ. For an instance of the first sort of process, take the one known as ‘Thomson's lamp’. Thomson's lamp is basically a device consisting of a lamp and a switch set on an electrical circuit. The switch can be in one of just two positions and the lamp has got to be lit — when the switch is in position ‘on’ — or else dim — when the switch is in position ‘off’. Assume that initially (at t = 12 A.M., say) the lamp is dim and that it is thenceforth subject to the following infinite sequence of actions: when half of the time remaining until t* = 1 P.M. has gone by, we carry out the action a1 of turning the switch into position ‘on’ and, as a result, the lamp is lit (a1 is thus performed at t = 1/2 P.M.); when half the time between the performance of a1 and t* = 1 P.M. has gone by, we carry out action a2 of turning to the switch into position ‘off’ and, as a result, the lamp is dim (a2 is thus performed at t = 1/2 + 1/4 P.M.); when half the time between the performance of a2 and t* = 1 P.M. has gone by, we carry out the action of turning the switch into position ‘on’ and, as a result, the lamp is lit (a3 is thus performed at t = 1/2 + 1/4 + 1/8), and so on. When we get to instant t* = 1 P.M. we will have carried out an infinite sequence of actions, that is, a supertask T = (a1, a2, a3, … , an, … ). If, for the sake of simplicity, we are only concerned about the evolution of the lamp (not the switch) the state of the world relevant to the description of our supertask admits of only two descriptions, one through the unitary set of sentences {lamp lit} and the other through the set {lamp dim}.
As an instance of the second sort of processes we referred to above, those about which no consensus has been reached as to whether they are supertasks, we can take the process which is described in one of the forms of Zeno's dichotomy paradox. Suppose that initially (at t = 12 A.M., say) Achilles is at point A (x = 0) and moving in a straight line, with a constant velocity v = 1 km/h, towards point B (x = 1), which is 1 km. away from A. Assume, in addition, that Achilles does not modify his velocity at any point. In that case, we can view Achilles's run as the performance of a supertask, in the following way: when half the time until t* = 1 P.M. has gone by, Achilles will have carried out the action a1 of going from point x = 0 to point x = 1/2 (a1 is thus performed in the interval of time between t =12 A.M. and t = 1/2 P.M.), when half the time from the end of the performance of a1 until t* = 1 P.M. will have elapsed, Achilles will have carried out the action a2 of going from point x = 1/2 to point x = 1/2 + 1/4 (a2 is thus performed in the interval of time between t = 1/2 P.M. and t = 1/2 + 1/4 P.M.), when half the time from the end of the performance of a2 until t* = 1 P.M. will have elapsed, Achilles will have carried out the action a3 of going from point x = 1/2 + 1/4 to point x = 1/2 + 1/4 + 1/8 (a3 is thus performed in the interval of time between t = 1/2 + 1/4 P.M. and t = 1/2 + 1/4 + 1/8 P.M.), and so on. When we get to instant t* = 1 P.M., Achilles will have carried out an infinite sequence of actions, that is, a supertask T = (a1, a2, a3, … , an, … ), provided we allow the state of the world relevant for the description of T to be specified, at any arbitrary instant, by a single sentence: the one which specifies Achilles's position at that instant. Several philosophers have objected to this conclusion, arguing that, in contrast to Thomson's lamp, Achilles's run does not involve an infinity of actions (acts) but of pseudo-acts. In their view, the analysis presented above for Achilles's run is nothing but the breakdown of one process into a numerable infinity of subprocesses, which does not make it into a supertask. In Allis and Koetsier's words, such philosophers believe that a set of position sentences is not always to be admitted as a description of the state of the world relevant to a certain action. In their opinion, a relevant description of a state of the world should normally include a different type of sentences (as is the case with Thomson's lamp) or, in any case, more than simply position sentences.
2. On The Conceptual Possibility Of Supertasks
In section 1.2 I have pointed out and illustrated the fundamental philosophical problem posed by supertasks. Obviously, one will only consider it a problem if one deems the concepts employed in its formulation acceptable. In fact, some philosophers reject them, because they regard the very notion of supertask as problematic, as leading to contradictions or at least to insurmountable conceptual difficulties. Among these philosophers the first well-known one is Zeno of Elea.
2.1 Zeno's Dichotomy Paradox
Consider the dichotomy paradox in the formulation of it given in section 1.3. According to Zeno, Achilles would never get to point B (x = 1) because he would first have to reach the mid point of his run (x = 1/2), after that he would have to get to the mid point of the span which he has left (x = 1/2 + 1/4), and then to the mid point of the span which is left (x = 1/2 + 1/4 + 1/8), and so on. Whatever the mid point Achilles may reach in his journey, there will always exist another one (the mid point of the stretch that is left for him to cover) that he has not reached yet. In other words, Achilles will never be able to reach point B and finish his run. According to Owen (Owen 1957–58), in this as well as in his other paradoxes, Zeno was concerned to show that the Universe is a simple, global entity which is not comprised of different parts. He tried to demonstrate that if we take to making divisions and subdivisions we will obtain absurd results (as in the dichotomy case) and that we must not yield to the temptation of breaking up the world. Now the notion of supertask entails precisely that, division into parts, as it involves breaking up a time interval into successive intervals. Therefore, supertasks are not feasible in the Zenonian world and, since they lead to absurd results, the notion of supertask itself is conceptually objectionable.
In stark contrast to Zeno, the dichotomy paradox is standardly solved by saying that the successive distances covered by Achilles as he progressively reaches the mid points of the spans he has left to go through — 1/2, 1/4, 1/8, 1/16, … — form an infinite series 1/2 + 1/4 + 1/8 + 1/16 + … whose sum is 1. Consequently, Achilles will indeed reach point B (x = 1) at t* = 1 P.M. (which is to be expected if he travels with velocity v = 1 km/h, as has been assumed). Then there is no problem whatsoever in splitting up his run into smaller sub-runs and, so, no inherent problem about the notion of supertask. An objection can be made, however, to this standard solution to the paradox: it tells us where Achilles is at each instant but it does not explain where Zeno's argument breaks down. Importantly, there is another objection to the standard solution, which hinges on the fact that, when it is claimed that the infinite series 1/2 + 1/4 + 1/8 + 1/16 + … adds up to 1, this is substantiated by the assertion that the sequence of partial sums 1/2, 1/2 + 1/4, 1/2 + 1/4 + 1/8, … has limit 1, that is, that the difference between the successive terms of the sequence and number 1 becomes progressively smaller than any positive integer, no matter how small. But it might be countered that this is just a patch up: the infinite series 1/2 + 1/4 + 1/8 + … seems to involve infinite sums and thus the performance of a supertask, and the proponent of the standard solution is in fact presupposing that supertasks are feasible just in order to justifiy that they are. To this the latter might reply that the assertion that the sum of the series is 1 presupposes no infinite sum, since, by definition, the sum of a series is the limit to which its partial (and so finite) sums approach. His opponent can now express his disagreement with the response that the one who supports the standard solution is deducing a matter of fact (that Achilles is at x = 1 at t* = 1 P.M.) from a definition pertaining to the arithmetic of infinite series, and that it is blatantly unacceptable to deduce empirical propositions from mere definitions.
2.2 The Inverse Form Of The Dichotomy Argument
Before concluding our discussion of the arguments connected with Zeno's dichotomy paradox which have been put forward against the conceptual feasibility of supertasks, we should deal with the so-called inverse dichotomy of Zeno, which can also be formulated as a supertask, but whose status as a logical possibility seems to some philosophers to be even more doubtful than that of the direct version expounded in section 2.1. The process involved in the paradox of inverse dichotomy admits of a supertask kind of description, as follows. Suppose that at t = 12 A.M. Achilles is at point A (x = 0) and wishes to do the action of reaching point B (x = 1). In order to do this action he must first of all go from point A to the mid point b1 (x = 1/2) of the span AB that he wishes to cover. In order to do this, he must in turn first do the action of going from point A to the mid point b2 (x = 1/4) of the span Ab1 that he wishes to cover, and so on . In order to reach B, Achilles will have to accomplish an infinite sequence of actions, that is, a supertask T* = (… , an, … , a3, a2, a1), provided we allow the state of the world relevant to the description of T* to be specified, at a given arbitrary instant, by a single sentence, the one specifying Achilles's position at that instant. Notice in the first place that T* has the same type of order as the natural order of negative integers: … , −n, … , −3, −2, −1 (such order type is usually denoted with the expression ‘w*’ and the related supertasks can therefore be called supertasks of type w*). The philosophical problem connected with supertasks of type w, already discussed in section 1.2 above, does not arise now because the set of sentences which describes the relevant state of the world after the performance of supertask T* is obviously a1(S), with S the set of sentences describing the initial relevant state of the world. But as the successive states of the world after S in relation to T* can be described by means of the infinite sequence of sets of sentences … , an(S), … , a3(S), a2(S), a1(S), some philosophers think it puzzling and unacceptable that the initial set of sentences in that sequence cannot be specified. This really means that we cannot specify which is the action in supertask T* that should be carried out first and that we consequently ignore how to begin. Isn't that proof enough that supertasks of type w* are impossible? Chihara (1965), for example, says that Zeno's inverse dichotomy is even more problematic than the direct one, since Achilles is supposed to be capable of doing something akin to counting the natural numbers in reverse order. In his opinion, it is just as impossible for Achilles to start his run — if viewed as a supertask of type w* — as it is to start this reverse counting process.
2.3 On Thomson's Impossibility Arguments
Thomson (1954–55) was convinced that he could show supertasks to be logically impossible. To this end, he made up the lamp example analysed in section 1.3, since known as ‘Thomson's lamp’. Thomson argued that the analysis of the workings of his lamp leads to contradiction, and therefore the supertask involved is logically impossible. But then, to the extent that this supertask is representative of ‘genuine’ supertasks, all genuine supertasks are impossible. Thomson's argument is simple. Let us ask ourselves what the state of the lamp is at t* = 1 P.M. At that instant the lamp cannot be lit, the reason being the way we manipulate it: we never light the lamp without dimming it some time later. Nor can the lamp be dim, because even if it is dim initially, we light it and subsequently never dim it without lighting it back again some time later. Therefore, at t* = 1 P.M. the lamp can be neither dim nor lit. However, one of its functioning conditions is that it must be either dim or lit. Thus, a contradiction arises. Conclusion: Thomson's lamp or, better, the supertask consisting in its functioning is logically impossible. Now is Thomson's argument correct? Benacerraf (1962) detected a serious flaw in it. Let us in principle distinguish between the series of instants of time in which the actions ai of the supertask are performed (which will be called the t-series) and the instant t* = 1 P.M., the first instant after the supertask has been accomplished. Thomson's argument hinges on the way we act on the lamp, but we only act on it at instants in the t-series, and so what can be deduced logically from this way of acting will apply only to instants in the t-series. As t* = 1 P.M. does not belong to the t-series, it follows that Thomson's supposed conclusion that the lamp cannot be lit at t* is fallacious, and so is his conclusion that it cannot be dim at t*. The conditions obtaining in the lamp problem only enable us to conclude that the lamp will be either dim or else lit but not both at t* = 1 P.M., and this follows from the fact that this exclusive disjunction was presupposed from the start to be true at each and every instant of time, independently of the way in which we could act on the lamp in the t-series of instants of time. What cannot be safely inferred is which one of these two states—dim or lit—the lamp will be in at t* = 1 P.M. or, alternatively, the state of the lamp at t* = 1 P.M. is not logically determined by what has happened before that instant. This consequence tallies with what was observed in section 2.1 about the fallacy committed by adherents to the standard solution against Zeno: they seek to deduce that at instant t* = 1 P.M. Achilles will be at point B from an analysis of the sub-runs performed by him before that instant, that is, they assume that Achilles's state at t* follows logically from his states at instants previous to t*, and in so assuming they make the same mistake as Thomson.
Thomson (1954–55) put forward one more argument against the logical possibility of his lamp. Let us assign to the lamp the value 0 when it is dim and the value 1 when it is lit. Then lighting the lamp means adding one unity (going from 0 to 1) and dimming it means subtracting one unity (going from 1 to 0). It thus seems that the final state of the lamp at t* = 1 P.M., after an infinite, and alternating, sequence of lightings (additions of one unity) and dimmings (subtractions of one unity), should be described by the infinite series 1−1+1−1+1… If we accept the conventional mathematical definition of the sum of a series, this series has no sum, because the partial sums 1, 1−1, 1−1+1, 1−1+1−1, … , etc. take on the values 1 and 0 alternatively, without ever approaching a definite limit that could be taken to be the proper sum of the series. But in that case it seems that the final state of the lamp can neither be dim (0) nor lit (1), which contradicts our assumption that the lamp is at all times either dim or lit. Benacerraf's (1962) reply was that even though the first, second, third, … , n-th partial sum of the series 1−1+1−1+1… does yield the state of the lamp after one, two, three, … , n actions ai (of lighting or dimming), it does not follow from this that the final state of the lamp after the infinite sequence of actions ai must of necessity be given by the sum of the series, that is, by the limit to which its partial sums progressively approach. The reason is that a property shared by the partial sums of a series does not have to be shared by the limit to which those partial sums tend. For instance, the partial sums of the series 0.3 + 0.03 + 0.003 + 0.0003 + … are 0.3, 0.3 + 0.03 = 0.33, 0.3 + 0.03 + 0.003 = 0.333,… , all of them, clearly, numbers less than 1/3; however, the limit to which those partial sums tend (that is, the sum of the original series) is 0.3333… , which is precisely the number 1/3.
2.4 On Black's Impossibility Argument
Another one of the classical arguments against the logical possibility of supertasks comes from Black (1950–51) and is constructed around the functioning of an infinity machine of his own invention. An infinity machine is a machine that can carry out an infinite number of actions in a finite time. Black's aim is to show that an infinity machine is a logical impossibility. Consider the case of one such machine whose sole task is to carry a ball from point A (x = 0) to point B (x = 1) and viceversa. Assume, in addition, that initially (at t = 12 A.M., say) the ball is at A and that the machine carries out the following infinite sequence of operations: when half the time until t* = 1 P.M. has gone by, it does the action a1 of taking the ball from position A to position B (a1 is thus carried out at t = 1/2 P.M.); when half the time between the performance of a1 and t* = 1 P.M. has gone by, it does the action a2 of taking the ball from position B to position A (a2 is thus carried out at t = 1/2 + 1/4 P.M.); when half the time between the performance of a2 and t* = 1 P.M. has gone by, the machine does the action a3 of taking the ball from position A to position B (a3 is thus performed in t = 1/2 + 1/4 + 1/8 P.M.), and so on. When we get to instant t* = 1 P.M. the machine will have carried out an infinite sequence of actions, that is, a supertask T = (a1, a2, a3, … , an, … ). The parallelism with Thomson's lamp is clear when it is realised that the ball in position A corresponds to the dim lamp and the ball in position B corresponds to the lit lamp. Nevertheless, Black believes that by assuming that at each instant the ball is either in A or else in B (and note that assuming this means that the machine transports the ball from A to B and viceversa instantaneously, but we need not be worried by this, since all that we are concerned with now is logical or conceptual possibility, not physical possibility), he can deduce, by a totally different route from Thomson's based on the symmetrical functioning of his machine, a contradiction regarding its state at t* = 1 P.M.. However, Benacerraf's criticisms also applies to Black's argument. In effect, the latter hinges on how the machine works, and as this has only been specified for instants of time previous to t* = 1 P.M., it follows that what can be logically inferred from the functioning of the machine is only applicable to those instants previous to t* = 1 P.M.. Black seeks to deduce a contradiction at t* = 1 P.M. but he fails at the same point as Thomson: whatever happens to the ball at t* = 1 P.M. cannot be a logical consequence of what has happened to it before. Of course, one can always specify the functioning of the machine for instants t greater than or equal to 1 P.M. by saying that at all those instants the machine will not perform any actions at all, but that is not going to help Black. His argument is fallacious because he seeks to reach a logical conclusion regarding instant t* = 1 P.M. from information relative to times previous to that instant.. In the standard argument against Zeno's dichotomy one could similarly specify Achilles's position at t* = 1 P.M. saying, for instance, that he is at B (x = 1), but there is no way that this is going to get us a valid argument out of a fallacious one, which seeks to deduce logically where Achilles will be at t* = 1 P.M. from information previous to that instant of time.
2.5 Benacerraf's Critique and the Dichotomy Arguments
The cases dealt with above are examples of how Benacerraf's strategy can be used against supposed demonstrations of the logical impossibility of supertasks. We have seen that the strategy is based on the idea that
(I) the state of a system at an instant t* is not a logical consequence of which states he has been in before t* (where by ‘state’ I mean ‘relevant state of the world’, see section 1.1)
and occasionally on the idea that
(II) the properties shared by the partial sums of a series do not have to be shared by the limit to which those partial sums tend.
Since the partial sums of a series make up a succession (of partial sums), (II) may be rewritten as follows:
(III) the properties shared by the terms of a succession do not have to be shared by the limit to which that succession tends.
If we keep (I), (II) and (III) well in mind, it is easy not to yield to the perplexing implications of certain supertasks dealt with in the literature. And if we do not yield to the perplexing results, we will also not fall into the trap of considering supertasks conceptually impossible. (III), for instance, may be used to show that it is not impossible for Achilles to perform the supertasks of the inverse and the direct dichotomy of Zeno. Take the case of the direct dichotomy: the limit of the corresponding succession of instants of time t1, t2, t3, … at which each one of Achilles's successive sub-runs is finished can be the instant at which Achilles's supertask has been accomplished, even if such a supertask is not achieved at any one of the instants in the infinite succession t1, t2, t3, … (all of this in perfect agreement with (III)).
2.6 Conclusion
As a corollary it may be said that supertasks do not seem to be intrinsically impossible. The contradictions that they supposedly give rise to may be avoided if one rejects certain unwarranted assumptions that are usually made. The main such assumption, responsible for the apparent conceptual impossibility of supertasks, is that properties which are preserved after a finite number of actions or operations will likewise be preserved after an infinite number of them. But that is not true in general. For example, we saw in section 1.2 above that the relevant state of the world after the performance of a task T = (a1, a2, … , an) on the relevant state S was logically determined by T and by S (and was an(an−1(an−2(… (a2(a1(S)))…)))), but we have now learned that after the performance of a supertask T = (a1, a2, a3, …, an, …) it is not (that is the core of Benacerraf's critique). The same sort of uncritical assumptions seem to be in the origin of infinity paradoxes in general, in which certain properties are extrapolated from the finite to the infinite that are only valid for the finite, as when it is assumed that there must be more numbers greater than zero than numbers greater than 1000 because all numbers greater than 1000 are also greater than zero but not viceversa (Galileo's paradox). In conclusion, if some supertasks are paradoxical, it is not because of any inherent inconsistency of the notion of supertask. This opinion is adhered to by authors such as Earman and Norton (1996).
3. On The Physical Possibility Of Supertasks
We have gone through several arguments for the conceptual impossibility of supertasks and counterarguments to these. Those who hold that supertasks are conceptually possible may however not agree as to whether they are also physically possible. In general, when this issue is discussed in the literature, by physical possibility is meant possibility in relation with certain broad physical principles, laws or ‘circumstances’ which seems to operate in the real world, at least as far as we know. But it is a well-known fact that authors do not always agree about which those principles, laws or circumstances are.
3.1 Kinematical Impossibility
In our model of Thomson's lamp we are assuming that at each moment the switch can be in just one of two set positions (‘off’, ‘on’). If there is a fixed distance d between them, then clearly, since the switch swings an infinite number of times from the one to the other from t = 12 A.M. until t* = 1 P.M., it will have covered an infinite distance in one hour. For this to happen it is thus necessary for the speed with which the switch moves to increase unboundedly during this time span. Grünbaum has taken this requirement to be physically impossible to fulfil. Grünbaum (1970) believes that there is a sort of physical impossibility of a purely kinematical nature (kinematical impossibility) and describes it in more precise terms by saying that a supertask is kinematically impossible if:
a) At least one of the moving bodies travels at an unboundedly increasing speed,b) For some instant of time t*, the position of at least one of the moving bodies does not approach any defined limit as we get arbitrarily closer in time to t*.
It is clear then that the Thomson's lamp supertask, in the version presented so far, is kinematically (and eo ipso physically) impossible, since not only does the moving switch have to travel at a speed that increases unboundedly but also—because it oscillates between two set positions which are a constant distance d apart—its position does not approach any definite limit as we get closer to instant t* = 1 P.M., at which the supertask is accomplished. Nevertheless, Grünbaum has also shown models of Thomson's lamp which are kinematically possible. Take a look at Figure 1, in which the switch (in position ‘on’ there) is simply a segment AB of the circuit connecting generator G with lamp L. The circuit segment AB can shift any distance upwards so as to open the circuit in order for L to be dimmed. Imagine we push the switch successively upwards and downwards in the way illustrated in Figure 2, so that it always has the same velocity v = 1.
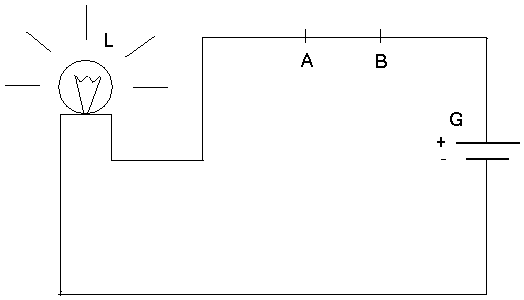
Figure 1
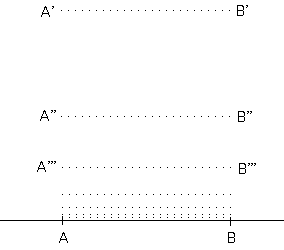
Figure 2
The procedure is the following. Initially (t = 0) the switch is in position A′B′ (lamp dim) a height of 0.2 above the circuit and moving downwards (at v = 1). At t = 0.2 it will be in position AB (lamp lit) and will begin moving upwards (v = 1). At t = 0.2 + 0.01 it will be in position A″B″ (lamp dim) and will begin moving downwards (v = 1). At t = 0.2 + 0.01 + 0.01 = 0.2 + 0.02 it will be in position AB (lamp lit) and will begin moving upwards (v = 1). At t = 0.2 + 0.02 + 0.001 it will be in position A′′′B′′′ (lamp dim), and so on. Obviously, between t = 0 and t* = 0.2 + 0.02 + 0.002 + … = 0.2222… = 2/9, the lamp is in the states ‘dim’ and ‘lit’ an infinite number of times, and so a supertask is accomplished. But this supertask is not kinematically impossible, because it has been so designed that the switch always moves with velocity v = 1 — and, therefore, condition (a) for kinematical impossibility is not fulfilled — and that, additionally, as we get closer to the limit time t* = 2/9 (the only one which could cause us any trouble) the switch approaches more and more a well-defined limit position, position AB (lamp lit)—and, therefore, condition (b) for kinematical impossibility is not fulfilled either. Once the kinematical possibility has been established, what is the state of the lamp at t* = 2/9? What has been said so far does not enable us to give a determinate answer to this question (just as the obvious kinematical possibility of Achilles's supertask in the dichotomy paradox does not suffice to determine where Achilles will be at t* = 1 P.M.), but there exists a ‘natural’ result. It seems intuitively acceptable that the position the switch will occupy at t* = 2/9 will be position AB, and so the lamp will be lit at that instant. There is no mysterious asymmetry about this result. Figure 3 shows a model of Thomson's lamp with a switch that works according to exactly the same principles as before, but which will yield the ‘natural’ result that the lamp will in the end be dim at t* = 2/9. In effect, the switch will now finally end up in the ‘natural’ position AB at t* = 2/9 and will thereby bring about an electrical short-circuit that will make all the current in the generator pass through the cable on which the switch is set, leaving nothing for the more resistant path where the lamp is.
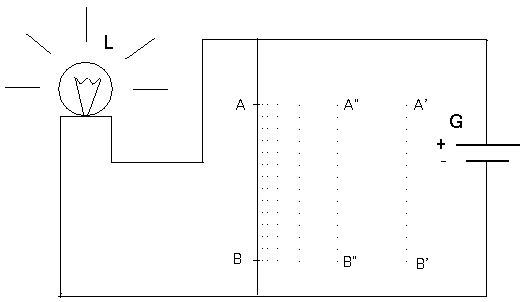
Figure 3
There are some who believe that the very fact that there exist Thomson's lamps yielding an intuitive result of ‘lamp lit’ when the supertask is accomplished but also other lamps whose intuitive result is ‘lamp dim’ brings up back to the contradiction which Thomson thought to have found originally. But we have nothing of that sort. What we do have is different physical models with different end-results. This does not contradict but rather corroborates the results obtained by Benacerraf: the final state is not logically determined by the previous sequence of states and operations. This logical indeterminacy can indeed become physical determinacy, at least sometimes, depending on what model of Thomson's lamp is employed.
A conspicuous instance of a supertask which is kinematically impossible is the one performed by Black's infinity machine, whose task it is to transport a ball from position A (x = 0) to position B (x = 1) and from B to A an infinite number of times in one hour. As with the switch in our first model of Thomson's lamp, it is obvious that the speed of the ball increases unboundedly (and so condition a) for impossibility is met), while at the same time, as we approach t* = 1 P.M., its position does not tend to any defined limit, due to the fact that it must oscillate continuously between two set positions A and B one unity distance apart from each other (and so also condition b) for impossibility is met).
3.2 The Principle Of Continuity and the Solution to the Philosophical Problem of Supertasks
Up to this point we have seen examples of supertasks which are conceptually possible and, among these, we have discovered some which are also physically possible. For the latter to happen we had to make sure that at least some requirements were complied with which, plausibly, characterise the processes that can actually take place in our world. But some definitive statement remains to be made about the philosophical problem posed by supertasks: what the state of the world is after they have been accomplished. The principles of physical nature which have so far been appealed to do not enable us to pronounce on this matter. The question thus arises whether some new principle of a physical nature can be discovered which holds in the real world and is instrumental in answering the question what the state of the world will be after a supertask. That discovery would allow us to resolve a radical indeterminacy which still persists—the reader will remember that even in the case of Achilles's dichotomy supertask we were quite unable to prove that it would conclude with Achilles in point B (x = 1). In Section 2.1 we saw that such proof cannot be obtained by recourse to the mathematical theory of infinite series exclusively; why should it be assumed that this abstract theory is literally applicable to the physical universe? After all, amounts of money are added up applying ordinary arithmetic but, as Black reminded us, velocities cannot be added up according to ordinary arithmetic.
Since Benacerraf's critique, we know that there is no logical connection between the position of Achilles at t* = 1 P.M. and his positions at instants previous to t* = 1 P.M. Sainsbury (1988) has tried to bridge the gap opened by Benacerraf. He claims that this can be achieved by drawing a distinction between abstract space of a mathematical kind and physical space. No distinction between mathematical and physical space has to be made, however, to attain that goal; one need only appeal to a single principle of physical nature, which is, moreover, simple and general, namely, that the trajectories of material bodies are continuous lines. To put it more graphically, what this means is that we can draw those trajectories without lifting our pen off the paper. More precisely, that the trajectory of a material body is a continuous line means that, whatever the instant t, the limit to which the position occupied by the body tends as time approaches t coincides precisely with the position of the body at t. Moreover, the principle of continuity is highly plausible as a physical hypothesis: the trajectories of all physical bodies in the real world are in fact continuous. What matters is that we realise that, aided by this principle, we can now finally demonstrate that after the accomplishment of the dichotomy supertask, that is, at t* = 1 P.M., Achilles will be in point B (x = 1). We know, in fact, that as the time Achilles has spent running gets closer and closer to t* = 1 P.M., his position will approach point x = 1 more and more, or, equivalently, we know that the limit to which the position occupied by Achilles tends as time get progressively closer to t* = 1 P.M. is point B (x = 1). As Achilles's trajectory must be continuous, by the definition of continuity (applied to instant t = t* = 1 P.M.) we obtain that the limit to which the position occupied by Achilles tends as time approaches t* = 1 P.M. coincides with Achilles's position at t* = 1 P.M. Since we also know that this limit is point B (x = 1), it finally follows that Achilles's position at t* = 1 P.M. is point B (x = 1). Now is when we can spot the flaw in the standard argument against Zeno mentioned in section 2.1, which was grounded on the observation that the sequence of distances covered by Achilles (1/2, 1/2 + 1/4, 1/2 + 1/4 + 1/8, … ) has 1 as its limit. This alone does not suffice to conclude that Achilles will reach point x = 1, unless it is assumed that if the distances run by Achilles have 1 as their limit, then Achilles will as a matter of fact reach x = 1, but assuming this entails using the principle of continuity. This principle affords us a rigorous demonstration of what, in any event, was already plausible and intuitively ‘natural’: that after having performed the infinite sequence of actions (a1, a2, a3, … , an, … ) Achilles will have reached point B (x = 1). In addition, now it is easy to show how, with a switch like the one in Figure 2, Thomson's lamp in Figure 1 will reach t* = 2/9 with its switch in position AB and will therefore be lit. We have in fact already pointed out (3.1) that in this case, as we get closer to the limit time t* = 2/9, the switch indefinitely approaches a well-defined limit position—position AB. Due to the fact that the principle of continuity applies to the switch, because it is a physical body, this well-defined limit position must coincide precisely with the position of the switch at t* = 2/9. Therefore, at t* = 2/9 the latter will be in positon AB and, consequently, the lamp will be lit. By the same token, it can also be shown that the lamp in Figure 3 will be dim at time t* = 2/9.
3.3 The Postulate of Permanence
In Section 3.2, the principle of continuity helped us find the final state resulting from the accomplishment of a supertask in cases in which there exists a ‘natural’ limit for the state of the physical system involved as time progressively approaches the instant at which the supertask is achieved. Now it is considerably more problematic to apply this principle to supertasks for which there is no ‘natural’ limit. For an example, let us consider Black's infinity machine, introduced in Section 2.4, and let us ask ourselves where the ball will be at instant t* = 1 P.M. at which the supertask is achieved. We can set up a reductio ad absurdum type of argument, as follows. Assume that at t* = 1 P.M. the ball were to occupy position P, that it was in point P. According to the principle of continuity, it follows that the limit to which the position occupied by the ball tends as time approaches t* = 1 P.M. is precisely position P. We know, though, that Black's infinity machine makes the ball oscillate more and more quickly between the fixed points A (x = 0) and B (x = 1) as we get closer to t* = 1 P.M., so the position of the ball does not approach any definite limit as we get closer to t* = 1 P.M. This conclusion patently contradicts what follows from the principle of continuity. Therefore, the assumption that, after Black's supertask is achieved (t* = 1 P.M.), the ball is at point P leads to contradiction with the principle of continuity. Thus, the ball cannot be at point P at t* = 1 P.M., and as the point can be any, given that it has been chosen arbitrarily, the ball cannot be at any single one of the points, which means that at t* = 1 P.M. the ball has ceased to exist. This funny conclusion is consistent with the principle of continuity, as we have just seen, but it enters into contradiction with what could be termed the ‘postulate of permanence’: no material body (and by that we mean a given quantity of matter) can go out of existence all of a sudden, without leaving any traces. The postulate of permanence seems to characterise our world at least as evidently as the principle of continuity. Notice in particular that certain physical bodies (particles) may dematerialise, but that is not inconsistent with the postulate of permanence since such a dematerialisation leaves an energy trace (which is not true of Black's ball). Consequently, we can see that the case Black's infinity machine is one in which the principles of continuity and permanence turn out to be mutually inconsistent. As long as we do not give up any of them, we are forced to accept that such an infinity machine is physically impossible.
3.4 On Burke's Impossibility Argument
Burke (2000b) proposed a new argument for the physical impossibility of supertasks based on the idea that their execution would entail the possibility of violating Newton's first law: a body cannot alter its state of motion without some external force acting on it. He imagines a passive Achilles being moved successively by an infinite numerable set of machines Mn. My presentation differs in secondary details from Burke's to concentrate on the essential issues. For each positive integer n, Mn will only act on Achilles in an interval of time of the magnitude 1/n − 1/(n+1), and will proceed as follows: if at some moment Achilles is at point xn = 1/n2 then it will take him to the point xn+1 = 1/(n+1)2 in a time 1/n − 1/(n+1) and (vice versa) if at any time Achilles is at xn+1 = 1/(n+1)2 it will take him and transfer him to xn = 1/n2 in a time 1/n − 1/(n+1). Now suppose that Achilles places himself at x1 = 1 in t = 1. Presumably the machines Mn will act successively on him, collectively performing a supertask that will bring the warrior in t = 2 to rest at x = 0 (as, under the principle of continuity, Achilles' path must be continuous). Is this true? Burke appeals to the temporal symmetry of the physical laws involved to argue that, if this is the case, then the machines Mn must also be capable of taking Achilles to x1 = 1 in t = 1 if he is initially at rest at x = 0 in t = 0 (executing the reverse process to the previous one). But, says Burke, if Achilles is at rest at x = 0 in t = 0, the machines Mn will be incapable of taking him to x1 = 1 in t = 1 for the simple reason that each machine operates at a finite distance to the right of x = 0. So, none of them is capable of setting him in motion, which means that Achilles remains at x = 0 even after t = 0 (Newton's first law). This means that the reverse process is not physically possible and, for reasons of temporal symmetry, the direct one is not possible either. And as the direct process is a standard supertask, its physical impossibility justifies the physical impossibility of supertasks in general.
The argument is original and refuting it involves an idea important in the context of other problems associated with supertasks, as we shall see later on. The key lies in recognizing that the fact that no Mn can take Achilles away from x = 0 is not enough to conclude that, in the absence of any other possible influence, Achilles cannot leave x = 0. We might consider the set of Mn as a new machine, ‘super M’, which obviously can exert a non-null force on Achilles at points arbitrarily close to x = 0 (unlike any individual machine). The Mn are individually incapable of setting somebody (Achilles) to their left in motion, but it does not follow that they are also incapable of doing so collectively. Burke's argument fails here. Furthermore (as Pérez Laraudogoitia argues in (2006a) and is immediately verifiable) we can design machines M*n capable of guaranteeing that, by handling Achilles exactly as the Mn would, an Achilles at rest at x = 0 in t = 0 would be taken by them to x1 = 1 in t = 1. It is enough to program each M*n thus: whatever the point at which Achilles is at in the instant tn+1 = 1/(n+1), it shall take him to xn = 1/n2 in the instant tn = 1/n.
4. The Physics of Supertasks
As we do not know exactly what laws of nature there are, it goes without saying that the question whether a particular supertask is physically possible (that is, compatible with those laws) cannot be given a definitive answer in general. What we have done in 3 above is rather to set out necessary conditions for physical possibility which are plausible (such as the principle of continuity) and sufficient conditions for physical impossibility which are likewise plausible (such as Grünbaum's criterion of kinematical impossibility). In this section we shall look into a problem related to the one just dealt with, but one to which a definitive answer can be given: the problem of deciding whether a certain supertask is possible within the framework of a given physical theory, that is, whether it is compatible with the principles of that theory. These are two distinct problems. At this stage our object are theories whereas in 3 above we were concerned with the real world. What we are after is supertasks formulated within the defined framework of a given physical theory which can tell us something exciting and/or new about that theory. We will discover that this search will lead us right into the heart of basic theoretical problems.
4.1 A New Form of Indeterminism: Spontaneous Self-Excitation
Classical dynamics is a theory that studies the motion of physical bodies which interact among themselves in various ways. The vast majority of interesting examples of supertasks within this theory have been elaborated under the assumption that the particles involved only interact with one another by means of elastic collisions, that is, collisions in which no energy is dissipated. We shall see here that supertasks of type w* give rise to a new form of indeterministic behaviour of dynamical systems. The most simple type of case (Pérez Laraudogoitia 1996) is illustrated by the particle system represented in Figure 4 at three distinct moments. It consists of an infinite set of identical point particles P1, P2, P3, … , Pn, … arranged in a straight line. Take the situation depicted in Figure 4A first. In it P1 is at one unity distance from the coordinate origin O, P2 at a distance 1/2 of O, P3 at a distance 1/3 of O and so on. In addition, let it be that all the particles are at rest, except for P1, which is approaching O with velocity v = 1. Suppose that all this takes place at t = 0. Now we will employ
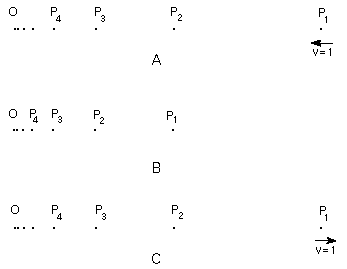
Figure 4
the well-known dynamic theorem by which if two identical particles undergo an elastic collision then they will exchange their velocities after colliding. If our particles P1, P2, P3, … collide elastically, it is easy to predict what will happen after t = 0 with the help of this theorem. In the event that P1 were on its own, it would reach O at t = 1, but in fact it will collide with P2 and lie at rest there, while P2 will acquire velocity v = 1. If P1 and P2 were on their own, then it would be P2 that would reach O at t = 1, but P2 will in fact collide with P3, and lie at rest there, while P3 will acquire velocity v = 1. Again, it can be said that if P1, P2 and P3 were on their own, then it is P3 that would reach O at t = 1, but in actual fact it will collide with P4 and lie at rest there, while P4 will acquire velocity v = 1, and so on. From the foregoing it follows that no particle will get to O at t = 1, because it will be impeded by a collision with another particle. Therefore, at t = 1 all the particles will already lie at rest, which yields the configuration in Figure 4B. Since P1 stopped when it collided with P2, it will occupy the position P2 had initially (at t = 0). Similarly, P2 stopped after colliding with P3 and so it will occupy the position P3 had initially (at t = 0), … , etc. If we view each collision as an action (which is plausible, since it involves a sudden change of velocities), it turns out that between t = 0 and t = 1 our evolving particle system has performed a supertask of type w. The second dynamic theorem we will make use of says that if a dynamic process is possible, then the process resulting from inverting the direction in which all the bodies involved in it move is also possible. Applying this to our case, if the process leading from the system in the situation depicted in Figure 4A to the situation depicted in Figure 4B is possible (and we have just seen it is), then the process obtained by simply inverting the direction in which the particles involved move will also be possible. This new possible process does not bring the system from configuration 4B back to configuration 4A but rather changes it into configuration 4C (as the direction in which P1 moves must be inverted). As the direct process lasts one time unity (from t = 0 to t = 1), so will the inverse process, and as in the direct process the system performs a supertask of type w, in the inverse process it will perform one of type w*. What is interesting about this new supertask of type w*? What's interesting is that it takes the system from a situation (4B) in which all its component particles are at rest to another situation (4C) in which not all of them are. This means that the system has self-excited, because no external influence has been exerted on it, and, what is more, it has done so spontaneously and unpredictably, because the supertask can set off at any instant and there is no way of predicting when it will happen. We have found a supertask of type w* to be the source of a new form of dynamical indeterminism. The reason we speak of indeterminism is because there is no initial movement to the performance of the supertask. The system self-excites in such a way that each particle is set off by a collision with another one, and it is the ordinal type w* of the sequence of collisions accomplished in a finite time that guarantees movement, without the need for a ‘prime mover’. Now movement without a ‘prime mover’ is precisely what characterises the dynamical indeterminism linked to supertasks of type w*.
The previous model of supertask in the form of spontaneous self-excitation is valid in relativistic classical dynamics as well as non-relativistic classical dynamics and can also be extended—though not in a completely obvious way, see Pérez Laraudogoitia (2001)—to the Newtonian theory of universal gravitation. The core idea behind indeterministic behaviour in all these cases is that the configuration of a physical system consisting of a denumerable infinite number of parts can be such that the solutions to the dynamic equations—in principle, one for each one of the parts—turn out to be coupled. A particular case of this situation (but probably the most important case, as it is the one that can be generalised more straightforwardly) is that in which the connection between solutions stems from the fact that the dynamic equations themselves are coupled as a result of the configuration of the system. Norton (1999) has availed himself of precisely this possibility, thus introducing a model of spontaneous self-excitation in quantum mechanics. Even though the indeterminism vanishes in this case when the normalizability of the state vector is imposed, this does not make his proposal any less interesting: after all, the free particle solutions to Schrodinger's equation are not normalizable either.
For reference purposes, we shall call the type of spontaneous self-excitation we have considered until now a type I self-excitation, which is characterized by the fact that the internal energy of an isolated system of particles changes (increases) suddenly and unpredictably. But the physics of supertasks allows, in the specific case of non-relativistic classical dynamics, a qualitatively different variety of self-excitation that we shall call a type II self-excitation: this is the self-excitation of a void (Pérez Laraudogoitia, 1998). To see how it works, we should remember once again the configuration of Figure 4B, which we modify trivially in two steps: a) by ensuring all the particles Pi are at rest in xi = (1/(i+1)) − 1 = − i/(i+1), which means taking them en bloc one unit to the left and b) by simultaneously placing a numerable infinity of particles P*i (identical to Pi) at rest at x*i = i/(i+1). The resulting configuration is symmetrical with respect to the origin of coordinates O, with the asterisk particles to the right and the non-asterisk ones to the left. We already know that both the set of particles to the left of the origin and the set of particles to the right may spontaneously and unpredictably self-excite provoking the successive movement of the particles at any velocity (for the sake of brevity we shall then say they self-excite at the particular velocity in question). Suppose now that: 1) in t = 1 the particles on the left self-excite at velocity v = 2 (the excitation will extinguish in t = 1+1), 2) in t = 1+1 the particles to the right self-excite at velocity v = 4 (the excitation will extinguish in t = 1+1+(1/2)), 3) in t = 1+1+(1/2)) the particles on the left self-excite at velocity v = 8 (the excitation will extinguish in t = 1+1+(1/2)+(1/4)), 4) in t = 1+1+(1/2)+(1/4) the particles on the right self-excite at at velocity v = 16 (the excitation will extinguish in t = 1+1+(1/2)+(1/4)+(1/8)), and so on successively. In t = 1+1+1 = 3 a numerable infinity of self-excitations of type I will have occurred. During this (finite) time, any one particle will have oscillated an infinite number of times between its initial position and the position of the particle to its right that was initially closest to it. As there is a finite distance between these two positions that will have been covered an infinite number of times in a finite time, the particle in question essentially evolves like Black's particle analyzed in section 2.4. It will therefore disappear in t = 3. In other words, in t = 3 the infinity of particles Pi, P*i will have disappeared leaving a void. By now performing the temporal reversion of this whole process of disappearance, what occurs is in fact a complex process of self-excitation of the void by means of which, spontaneously and unpredictably, there emerges a numerable infinity of identical particles. This is an example of type II self-excitation. The disappearance in t = 3 of the infinity of particles Pi, P*i certainly violates the Postulate of Permanence introduced in section 3.3 (and also the necessary conditions for kinematic possibility of Grünbaum, as seen in section 3.1) but what is important here is that it does not violate any of the postulates of classical mechanics. In particular, the standard formulation of the principle of conservation of mass: ‘Particle World lines do not have beginning or end points and mass is constant along a World line’ (Earman 1986) is not contradicted, because none of the World lines of particles Pi, P*i genuinely has an end point.
Until now we have only seen examples of self-excitations in systems of infinite mass, but this is not an essential condition. Taking advantage of the structural similarity between the equations of the dynamics of translation and the dynamics of rotation, Pérez Laraudogoitia (2007a) proposed an analogous model to the one in Figure 4, but in the dynamics of rotation, in which, instead of infinite particles of equal mass placed in a line, infinite rectangular-shaped thin rigid rods of equal momentum of inertia are included in one another. Despite having a finite mass, this system may self-excite as simply as the one in Figure 4B, although its spatial extension must be infinite to maintain the condition of equal momentums of inertia. Atkinson (2007) proved that the spatially limited system of particles in Figure 4B can also spontaneously self-excite in classical mechanics when the mass of Pn is mn = (2/(n+1)) − (2/(n+2)), which obviously corresponds to a total mass of unit value. Finally, Pérez Laraudogoitia (2007b) showed that, for this same system but in the relativistic case, the spontaneous self-excitation is possible providing qn+1 = (kqn+k)/(1+k+k2−kqn) (where qn = mn+1/mn, with 0 < k < 1), and which also corresponds to a case of total finite mass if q1 < k.
4.2 A New Form of Indeterminism: Global Interaction
A simple modification of the initial conditions illustrated in Figure 4A leads to a qualitatively different type of supertask that is interesting in itself. Now suppose that all the particles P1, P2, P3, … are at rest at the beginning, while a new particle P0 (identical to them) approaches the origin O at unit velocity but from the left of O. Alper & Bridger (1998) were the first to consider this situation, arguing that it is incompatible with Newtonian mechanics. Their argument went like this: P0 cannot hit Pi because in order to do so P0 must have passed through Pi+1, the particle lying immediately to the left of Pi. Therefore P0 cannot hit any particle. On the other hand, if P0 does not hit any particle, then its motion is undisturbed, and it arrives at, for example, position x = 1/2 at a certain instant of time. But there is a particle, namely P2, at x = 1/2. P0 must hit P2, contradicting the conclusion that P0 hits none of the particles. As Pérez Laraudogoitia (2005) underscored, this argument is fallacious. To see why, consider the innocent example of the collision between two identical solid spheres (of, let us say, unit ratio), X and Y. Let us suppose that Y is mentally divided into an infinite number of concentric spheres Yi in the following way: Y1 is a solid sphere of radius 1/2 and Yi (i > 1) is a hollow sphere of interal radius (i−1)/i and external radius i/(i+1). Clearly, although X collides with Y it does not collide with any of the Yi (Yi is pushed at most by Yi+1 and Yi−1) and this despite the fact that Y is the set of Yis. This may seem enigmatic at first sight, largely because we tend to pass inadvertently from
(A) If X collides with Y then at least one division into parts of Y exists such that X collides with one of the parts
which is true, to
(B) If X collides with Y then for all divisions into parts of Y, X collides with one of the parts
which is false. In the process, one goes fallaciously from an existential to a universal statement, and after wrongly settling on (B), one finds it impossible for X to collide with Y given the division of Y into Yi parts, none of which collides with X. One then commits a fallacy of composition by assuming here that the whole must have the properties of its parts: if none of the Yi parts collides with X then Y cannot collide with X. Of course Y collides with X, and as Y is the set of Yis it turns out that X collides with the set of Yis, but does not collide with any Yi separately. One can say that X collides collectively, but not distributively, with the set of Yis and, in more physical terms, that X interacts (collides) globally with the Yis. We thus recover the idea of collective action seen in the analysis of Burke's argument concerning impossibility in 3.4. The fact that the Yis were obtained by a process of mental division of Y is irrelevant. One may convert them, if one so desires, into ‘physical’ parts by supposing that Yi is made from matter with density i/(i+1). The conclusion, then, is that a physical system S1 can collide (globally) with another system S2 without colliding with any of the physical parts of which S2 is made. Now the error in Alper and Bridger's argument becomes clear: the particle P0 collides (globally) with the set of the Pi (i > 0) without doing so with any separately, which means that their statement ‘if P0 does not hit any particle, then its motion is undisturbed’ is not justified. This of course means that the conclusion (based on the foregoing statement) that their system is incompatible with Newtonian mechanics is not justified either.
Indeed, the global collision of P0 with the set of the Pi leads to a new form of indeterminism. If, as in a typical elastic collision, we impose the classical laws of the conservation of energy and linear momentum, then one possible evolution from the instant of the global collision is one in which P0 excites the infinite system of the Pi (i > 0) at unit velocity (remember the terminology of section 4.1) before coming to rest and P1 finally moving away from origin O at that unit velocity. But there is also the possibility of P0 rebounding backwards after its global collision to provoke the excitation of the system of the Pi at not one but two different velocities. For instance, readers may verify that the laws of conservation referred to are observed in Newtonian mechanics if, in the final state, P0 moves away from the origin O to the left at velocity 1/4 whereas finally P1 moves away to the right at velocity (5+51/2)/8 and P2 at velocity (5−51/2)/8 while the other Pi come to rest. It is not difficult to verify that the global collision of P0 could also excite the system of the Pi with any number greater than 2 of different velocities. Having seen in section 4.1 that the self-excitation of a dynamical system entailed a new source of indeterminism, we now verify that global interaction provides another, different source, although linked to the previous one by the fact that it causes excitations that, in absence of external influences, could be spontaneous.
Peijnenburg & Atkinson (2008 and forthcoming) also analyzed the problem proposed by Alper & Bridger (1998), proposing a different solution, although still closely linked to the previous one. They reject the latter's path to contradiction at the same point at which Pérez Laraudogoitia (2005) does, namely: ‘if P0 does not hit any particle, then its motion is undisturbed’ is not justified. But their rejection has another formulation. They propose distinguishing between ‘collision’ as ‘ making contact’ (when two bodies X and Y collide, then X and Y come in contact with one another, in the sense that at least one point of X occupies the same location in space as does one point of Y) and ‘collision’ as ‘zero distance’. Although both notions coincide in topologically closed bodies, this is not the case when topologically open bodies are involved, like the set of particles Pi (i > 0). In the instant P0 arrives at the origin O it does not collide with the other particles in the first sense of ‘making contact’. But under the definition of ‘ collision’ as ‘zero distance ’, P0 does indeed collide with the set of stationary balls at the origin O. Although Peijnenburg & Atkinson's treatment might seem equivalent to Pérez Laraudogoitia's, it is in fact less general, as there are cases of global interaction that it can't account for. Simplifying the model proposed in Pérez Laraudogoitia (2006b), let us assume that for t < 0 we have, in the plane z = 0, a rigid disc D of radius r = 2 at rest and centred on the origin, and above it, in the plane z = 1, we have in t = 0 a denumerable infinite set of rigid rings Ri of equal mass, null thickness, radii ri = i/(i+1) and velocities vi = i moving towards D. In no instant subsequent to t = 0 may D still be in the plane z = 0, because in that case it would have been ‘pierced through’ by an infinite number of rigid rings. This means that, in t = 0, D interacts globally with the infinite set of Ri in Pérez Laraudogoitia's sense, despite the fact that, the distance between D and the Ri being equal in this instant to the unit, D cannot collide with the Ri in any of the senses considered by Peijnenburg & Atkinson. Peijnenburg & Atkinson's analysis fails when faced with situations like this, demonstrating that it is not sufficiently general.
4.3 Energy and Momentum Conservation in Supertasks
In sections 4.1 and 4.2 we considered the problem of indeterminism in supertasks formulated principally in the sphere of classical mechanics or relativistic mechanics. This section provides a brief review of the closely related issue of energy and momentum conservation in supertasks generated from initial states topologically similar to the ones in Figure 4A in the following precise sense: P1 may have any velocity (towards the left) while the rest of the particles will be at rest to the left of P1 in arbitrary positions on P1's line of advance (but with Pj to the left of Pi if j > i) and such that these positions have a point of accumulation O.
From 4.1 it obviously follows that when the total mass is infinite both energy conservation and momentum conservation may be violated (in classical and relativistic mechanics alike). They are violated, for instance, when all the particles are identical. Atkinson (2007) proposed the first model with total finite mass in Newtonian mechanics in which the energy was not conserved, although momentum was, and showed that in this mechanics momentum will be conserved provided that: C1) total mass is finite, C2) if j > i the mass of Pj is less than those of the Pi, and C3) each particle Pn+1 undergoes in the process exactly two collisions (one with each of its immediate neighbours) while P1 undergoes just one. He also demonstrated that, in relativistic mechanics and under these same three conditions, energy conservation will be violated if and only if momentum conservation is violated (in marked contrast to the classical case), and that such violations will in fact take place unless the masses of the particles Pn decrease very rapidly with n (Atkinson 2008 shows that violation will occur, for example, if mn = 2−n·m0). Finally, Atkinson & Johnson (forthcoming) have shown that the temporal reversal of the state resulting from a process performed under conditions C1), C2) and C3) lead in turn to an indeterministic process: there is an arbitrary parameter in the general solution to the equations of the particles' movement that corresponds to the injection of an arbitrary amount of energy (classically), or energy-momentum (relativistically), into the system at the point of accumulation of the locations of these particles. This last, highly general result poses the question of whether in the classical (or relativistic) dynamics of supertasks there is an intrinsic connection between indeterminism and the non-conservation of energy. Pérez Laraudogoitia (2009a) proves there isn't by showing a specific example of supertask (although qualitatively different from the ones considered by Atkinson & Johnson) in which the energy is conserved despite the evolution of the physical system analized being indeterministic. This latter model is also of interest because it remains valid when the rigid bodies assumed in its description are replaced, whether classically or relativistically, by deformable solids. Furthermore, as the total mass may be as small as one wishes without affecting the description of the evolution, it might be argued that even the inclusion of gravitation will not affect the results. This is probably the clearest example of how supertasks are possible in the context of specific physical theories that also make realistic assumptions.
4.4 Actions without Interaction
The configuration of identical particles introduced in section 4.1, and the resulting possibility of spontaneous self-excitation, has inspired a new type of problem that can be formulated in terms of supertasks (although not only in terms of supertasks), that is qualitatively different to the ones considered until now. It is a commonplace that, when we act physcally on a system (which entails exerting influence in some way on its evolution), we do so by interacting with it. However, Pérez Laraudogoitia (2009b) has shown that a numerable infinity of actors (Gods, or machines suitably programmed) may act physically on an infinite set of particles provoking its self-excitation without interacting with the set in question. Let us consider the system of identical particles in Figure 4A, with the sole difference that P1 is also at rest (in general, Pi is at rest at xi = 1/i). We know that it may spontaneously self-excite at any moment at any velocity, although we shall assume that in t = 0 all the Pi are at rest. Let God1, God2, God3, … be a numerable totality of Gods (machines) such that Godn has the capacity to control particle Pn and only particle Pn. Taking t* > 0, let us suppose that the Gods now decide to pursue the following course of action: Godn shall prevent, at any 0 < t < t* + (1/n), Pn from abandoning point xn = 1/n, but if, from t* + (1/n), Pn does not acquire a unit velocity towards the right by other means (although even for a limited time) then it (Godn) shall provide it (n = 1, 2, 3, …). The interesting, and surprising, thing in this case is that the Gods will manage to make the system of particles self-excite at t* at unit velocity and they will do so without interacting with it, meaning we will indeed have a case of action without interaction that does, however, alter the dynamic state of the particles (all at rest in t = 0). This is easy to see in two steps:
(I) For every n, Pn will acquire from t* + (1/n) unit velocity to the right (although, for n > 1, for a limited time). This is so because, should there be no other process providing it with unit velocity from t* + (1/n), we know that Godn will provide it.
(II) For every n, Pn will acquire from t* + (1/n) unit velocity to the right as a result of receiving the impact of Pn+1. This is so because, according to (I), Pn+1 acquired from t* + (1/(n+1)) unit velocity to the right which led it to collide with Pn at t* + (1/(n+1)) + ((1/n) − (1/(n+1))) = t* + (1/n), transmitting that velocity to it from t* + (1/n), which implies that Godn does not in fact interact with Pn.
From (II) it follows that the set of particles will self-excite precisely at t*, that no Godn interacts with any particle, but that the set of Gods caused this self-excitation by acting physically without interaction on the set in question on the basis of the policy referred to earlier. Indeed, if only the particles existed (without Gods), then from the configuration in t = 0 an infinity of different possibilities of evolution would be open to them, an infinity that the Gods have reduced significantly by preventing any self-excitation before t* and provoking one in t*: this is precisely how they acted on them. From this Pérez Laraudogoitia (2009b) concludes that indeterminism is a necessary condition for actions without interaction.
4.5 The Spaceship Paradox
Benardete (1964) formulates what has since then come to be known as the spaceship paradox in the following terms: ‘Indeed one minute will suffice to enable us to exhaust an infinite world. We have only to launch a rocket and travel one thousand miles into outer space during the first 1/2 minute, another one thousand miles after that during the next 1/4 minute, still another one thousand miles during the next 1/8 minute, &c. ad infinitum . At the end of the minute we shall have succeeded in travelling an infinite distance’ (p. 149). The situation described here has all the characteristic ingredients of a classical supertask and the whiff of paradox arises when we wonder, like Benardete: ‘At the end of the minute we find ourselves an infinite distance from Earth … Where in the World are we?’ The question only makes sense in a Newtonian universe, where there is no limit to the velocity that a material body can achieve. Indeed, Pérez Laraudogoitia (1997) constructed a model of the spaceship paradox in classical particle mechanics in which a numerable infinity of identical particles, distributed along the positive X axis with unbounded velocities, collide with each other in an orderly fashion in a finite time, each transmitting to the following one progressively increasing velocities in accordance with a process essentially identical to the one imagined by Benardete. Oppy (2006) rejected the possibility of this kind of process, reasoning that there is no possible World in which the speed of the spaceship is infinite. However, his criticism is not convincing to the extent that in Benardete's scenario only the average velocity (and average acceleration) needs to be infinite, not the instantaneous velocity (or acceleration). In any case the air of paradox disappears if we apply coherently the principle of continuity seen in section 3.2. From that, it follows that at the end of the minute Benardete's spaceship will not be anywhere, as we saw occurring in section 4.1 with Black's particle introduced previously in section 2.4.
The temporal reversion of this curious evolution of a flight to infinity is an unpredictable process of arrival from infinity, which would appear to sanction an odd asymmetry between the two situations: the escape is deterministic while the arrival from infinity is not. However, Pérez Laraudogoitia (forthcoming) has shown that this asymmetry is much less profound than it appears. By elaborating an infinite sequence of suitably programmed finite tasks (which recall, although with far greater complexity, the ones taken on by the Gods in section 4.4 to achieve actions without interaction), it is possible to design supertasks capable of ‘bringing’ a spaceship from infinity in a perfectly planned and deterministic way. The intriguing possibility of manipulating the conditions at infinity to predict what we are going to ‘take’ from there (consistently, certainly, with the principle of mass conservation announced in section 4.1) is a further example of the new conceptual possibilities opened up by the supertask concept.
However, to date we have only discussed models of supertasks in classical mechanics, relativistic mechanics and quantum mechanics. The physics of supertasks in the context of the other major closed physical theory, general relativity, will be the topic of the following two subsections.
4.6 Bifurcated Supertasks
Within relativity theory, supertasks have been approached from a radically different perspective from the one adopted here so far. This new perspective is inherently interesting, since it links the problem of supertasks up with the relativistic analysis of the structure of space-time. To get an insight into the nature of that connection, let us first notice that, according to the theory of relativity, the duration of a process will not be the same in different reference systems but will rather vary according to the reference system within which it is measured. This leaves open the possibility that a process which lasts an infinite amount of time when measured within reference system O may last a finite time when measured within a different reference system O′.
The supertask literature has needed to exploit space-times with sufficiently complicated structure that global reference systems cannot be defined in them. In these and other cases, the time of a process can be represented by its ‘proper time’. If we represent a process by its world-line in space-time, the proper time of the process is the time read by a good clock that moves with the process along its world-line. A familiar example of its use is the problem of the twins in special relativity. One twin stays home on earth and grows old. Forty years of proper time, for example, elapses along his world-line. The travelling twin accelerates off into space and returns to find his sibling forty years older. But much less time — say only a year of proper time — will have elapsed along the travelling twin world-line if he has accelerated to sufficiently great speeds.
If we take this into account it is easily seen that the definition of supertask that we have been using is ambiguous. In section 1 above we defined a supertask as an infinite sequence of actions or operations carried out in a finite interval of time. But we have not specified in whose proper time we measure the finite interval of time. Do we take the proper time of the process under consideration? Or do we take the proper time of some observer who watches the process? It turns out that relativity theory allows the former to be infinite while the latter is finite. This fact opens new possibilities for supertasks. Relativity theory thus forces us to disambiguate our definition of supertask, and there is actually one natural way to do it. We can use Black's idea — presented in 2.4 — of an infinity machine, a device capable of performing a supertask, to redefine a supertask as an infinite sequence of actions or operations carried out by an infinity machine in a finite interval of the machine's own proper time measured within the reference system associated to the machine. This redefinition of the notion of supertask does not change anything that has been said until now; our whole discussion remains unaffected so long as ‘finite interval of time’ is read as ‘finite interval of the machine's proper time’. This notion of supertask, disambiguated so as to accord with relativity theory, will be denoted by the expression ‘supertask-1’. Thus:
Supertask-1: an infinite sequence of actions or operations carried out by an infinity machine in a finite interval of the machine's proper time.
However we might also imagine a machine that carries out an infinite sequence of actions or operations in an infinite machine proper time, but that the entire process can be seen by an observer in a finite amount of the observer's proper time.
It is convenient at this stage to introduce a contrasting notion:
Supertask-2: an infinite sequence of actions or operations carried out by a machine in a finite interval of an observer's proper time.
While we did not take relativity theory into account, the notions of supertask-1 and supertask-2 coincided. The duration of an interval of time between two given events is the same for all observers. However in relativistic spacetimes this is no longer so and the two notions of supertasks become distinct. Even though all supertasks-1 are also supertasks-2, there may in principle be supertasks-2 which are not supertasks-1. For instance, it could just so happen that there is a machine (not necessarily an infinity machine) which carries out an infinite number of actions in an interval of its own proper time of infinite duration, but in an interval of some observer's proper time of finite duration. Such a machine would have performed a supertask-2 but not a supertask-1.
The distinction between supertasks-1 and supertasks-2 is certainly no relativistic hair-splitting. Why? Because those who hold that, while conceptually possible, supertasks are physically impossible (this seems to be the position adopted by Benacerraf and Putnam (1964), for instance) usually mean that supertasks-1 are physically impossible. But from this, it does not follow that supertasks-2 must also be physically impossible. Relativity theory thus adds a brand-new, exciting extra dimension to the challenge presented by supertasks. Earman and Norton (1996), who have studied this issue carefully, use the name ‘bifurcated supertasks’ to refer specifically to supertasks-2 which are not supertasks-1, and I will adopt this term.
4.7 Bifurcated Supertasks and the Solution to the Philosophical Problem of Supertasks
What shape does the philosophical problem posed by supertasks — introduced in Section 1.2 — take on now? Remember that the problem lay in specifying the set of sentences which describe the state of the world after the supertask has been performed. The problem will now be to specify the set of sentences which describe the relevant state of the world after the bifurcated supertask has been performed. Before this can done, of course, the question needs to be answered whether a bifurcated supertask is physically possible. Given that we agree that compatibility with relativity theory is a necessary and sufficient condition of physical possibility, we can reply in the affirmative.
Pitowsky (1990) first showed how this compatibility might arise. He considered a Minkowski spacetime, the spacetime of special relativity. He showed that an observer O* who can maintain a sufficient increase in his acceleration will find that only a finite amount of proper time elapses along his world-line in the course of the complete history of the universe, while other unaccelerated observers would find an infinite proper time elapsing on theirs.
Let us suppose that some machine M accomplishes a bifurcated supertask in such a way that the infinite sequence of actions involved happens in a finite interval of an observer O's proper time. If we imagine such an observer at some event on his world-line, all those events from which he can retrieve information are in the ‘past light cone’ of the observer. That is, the observer can receive signals travelling at or less than the speed of light from any event in his past light cone. The philosophical problem posed by the bifurcated supertask accomplished by M has a particularly simple solution when the infinite sequence of actions carried out by M is fully contained within the past light cone of an event on observer O's world-line. In such a case the relevant state of the world after the bifurcated supertask has been performed is M's state, and this, in principle, can be specified, since O has causal access to it. Unfortunately, a situation of this type does not arise in the simple bifurcated supertask devised by Pitowsky (1990). In his supertask, while the accelerated observer O* will have a finite upper bound on the proper time elapsed on his world-line, there will be no event on his world-line from which he can look back and see an infinity of time elapsed along the world-line of some unaccelerated observer.
To find a spacetime in which the philosophical problem posed by bifurcated supertasks admits of the simple solution that has just been mentioned, we will move from the flat spacetime of special relativity to the curved spacetimes of general relativity. One type of spacetime in the latter class that admits of this simple solution has been dubbed Malament-Hogarth spacetime, from the names of the first scholars to use them (Hogarth 1992). An example of such a spacetime is an electrically charged black hole (the Reissner-Nordstroem spacetime). A well known property of black holes is that, in the view of those who remain outside, unfortunates who fall in appear to freeze in time as they approach the event horizon of the black hole. Indeed those who remain outside could spend an infinite lifetime with the unfortunate who fell in frozen near the event horizon. If we just redescribe this process from the point of view of the observer who does fall in to the black hole, we discover that we have a bifurcated supertask. The observer falling in perceives no slowing down of time in his own processes. He sees himself reaching the event horizon quite quickly. But if he looks back at those who remain behind, he sees their processes sped up indefinitely. By the time he reaches the event horizon, those who remain outside will have completed infinite proper time on their world-lines. Of course, the cost is high. The observer who flings himself into a black hole will be torn apart by tidal forces and whatever remains after this would be unable to return to the world in which he started.
5. What Supertasks Entail for the Philosophy of Mathematics
5.1 A Critique of Intuitionism
The possibility of supertasks has interesting consequences for the philosophy of mathematics. To start with, take a well-known unsolved mathematical problem, for example that of knowing whether Goldbach's conjecture is or is not correct. Goldbach's conjecture asserts that any even number greater than 2 is the sum of two prime numbers. Nobody has been capable of showing whether this is true yet, but if supertasks are possible, that question can be resolved. Let us, to that effect, perform the supertask of type w consisting in the following sequence of actions: action a1 involves checking whether the first pair greater than 2 (number 4) is the sum of two prime numbers or not; let this action be accomplished at t = 0.3 P.M.; action a2 involves checking whether the second pair greater than 2 (number 6) is the sum of two prime numbers or not; let this action be accomplished at t = 0.33 P.M.; action a3 involves checking whether the third pair greater than 2 (number 8) is the sum of two prime numbers or not; let this action be accomplished at t = 0.333 P.M., and so on. It is clear that at t = 0.33333… = 1/3 P.M., the instant at which the supertask has already been performed, we will have checked all the pairs greater than 2, and, therefore, will have found some which is not the sum of two prime numbers or else will have found all of them to be the sum of two prime numbers. In the first case, we will know at t = 1/3 P.M. that Goldbach's conjecture is false; in the second case we will know at t = 1/3 P.M. that it is true. Weyl (1949) seems to have been the first to point to this intriguing method —the use of supertaks—for settling mathematical questions about natural numbers. He, however, rejected it on the basis of his finitist conception of mathematics; since the performance of a supertask involves the successive carrying out of an actual infinity of actions or operations, and the infinity is impossible to accomplish, in his view. For Weyl, taking the infinite as an actual entity makes no sense. Nevertheless, there are more problems here than Weyl imagines, at least for those who ground their finitist philosophy of mathematics on intuitionism à la Brouwer. That is because Brouwer's rejection of actual infinity stems from the fact that we, as beings, are immersed in time. But this in itself does not mean that all infinities are impossible to accomplish, since an infinity machine is also ‘a being immersed in time’ and that in itself does not prevent the carrying out of the infinity of successive actions a supertask is comprised of. It goes without saying that one can adhere to a constructivist philosophy of mathematics (and the consequent rejection of actual infinity) for diferent reasons from Brouwer's; supertasks will still not be the right kind of objet to study either.
As Benacerraf and Putnam (1964) have observed, the acknowledgement that supertasks are possible has a profound influence on the philosophy of mathematics: the notion of truth (in arithmetic, say) would no longer be doubtful, in the sense of dependent on the particular axiomatisation used. The example mentioned earlier in connection with Goldbach's conjecture can indeed be reproduced and generalised to all other mathematical statements involving numbers (although, depending on the complexity of the statement, we might need to use several infinity machines instead of just one), and so, consequently, supertasks will enable us to decide on the truth or falsity of any arithmetical statement; our conclusion will no longer depend on provability in some formal system or constructibility in a more or less strict intuitionistic sense. This conclusion seems to lead to a Platonist philosophy of mathematics.
However, the situation here is more subtle than the previous comments suggest. Above I introduced a supertask of type w that can settle the truth or falsity of Goldbach's conjecture, but the reference (essential in it) to time contrasts with the lack of specification regarding how to make the necessary computations.When one tries to make up for this omission one discovers that the defence of Platonism is more debatable than it seems at first sight. Davies (2001) has proposed a model of an infinite machine (an infinite machine is a computer which can carry out an infinite number of computations within a finite length of time) based on the Newtonian dynamics of continuous media which reveals the nature of the difficulty. One cannot attempt to decide on mathematical questions such as Goldbach's conjecture by using a mechanical computer which carries out operations at an increasing speed, as if it were a Turing machine. The reason is that the different configurations the computer adopts at increasingly short intervals of time eventually (if the conjecture is true) lead to a paradox of the type of Thomson's lamp, where (if we do not assume continuity in the sense of section 3.2) the final state of the computer is indeterminate, which makes it useless for our purpose. Davies's clever solution consists in assuming an infinite machine capable of building a replica of itself that has twice its own memory but is smaller and works at greater speed. The replica can in its turn build another (even smaller and quicker) replica of itself and so on. With the details Davies gives about the working of his infinite machines, it is clear that they will in no case lead to an indeterminacy paradox (since each replica carries out only a finite part of the task).The problem is that to settle questions like Goldbach's conjecture (if, as I said above, it is true) a numerable (actual) infinity of replicating machines is required, and this will surely be rejected by anyone who, like intuitionists, has a strong dislike of the actual infinity. In more abstract words, the mathematical theory that models the computation process presupposes a Platonic conception of the infinite and thus begs the question by, circularly, supporting Platonism.
5.2 The Importance of the Malament-Hogarth Spacetime
Similar comments can be made about the implications of supertasks for the philosophy of mathematics if one only accepts the possibility of bifurcated supertasks. Of course, a bifurcated supertask performed in a non-Malament-Hogarth space-time would not be so interesting in this sense. The obvious reason is that we would not even have a sound procedure to determine the truth or falsity of Goldbach's conjecture seen in 5.1 by means of the performance of an infinite sequence of actions of order type w. To really have a safe decision procedure in this simple case (as in other, more complex ones) there must necessarily exist an instant of time at which it can be said that the supertask has been accomplished. Otherwise, in the event that the machine finds a counterexample to Goldbach's conjecture we will know it to be false, but in the event of the machine finding none we will not be able to tell that it is true, because for this there must exist an instant of time by which the supertask has been accomplished and at which we can say something like: ‘the supertask has been performed and the machine has found no counterexamples to Goldbach's conjecture; therefore, the conjecture is true’. It follows that, in the case of a bifurcated supertask, possessing a sound decision procedure on Goldbach's conjecture requires the existence of an observer O such that the infinite sequence of actions (of order type w) carried out by the machine lies within the past light cone of an event on observer O's world-line. But this is equivalent to saying that the relativistic space-time in which the bifurcated supertask is performed is a Malament-Hogarth space-time, and this realisation is one of the main reasons why this sort of relativistic space-times have been studied in the literature.
At first sight, the intuitionistic criticism of the possibility of supertasks is less effective in the case of bifurcated supertasks, because in this latter case it is not required that there is any sort of device capable of carrying out an infinite number of actions or operations in a finite time (measured in the reference system associated to the device in question, which is the natural reference system to consider). In contrast, from the possibility of bifurcated supertasks in Malament-Hogarth space-times strong arguments seem to follow against an intuitionistic philosophy of mathematics. But, again, one must be very cautious at this point, as we were at the end of our previous section 5.1. The mathematical theory which models a bifurcated supertask is general relativity, and this theory, as it fully embraces classical mathematical analysis, entails a strong commitment to the—intuitionistically unacceptable—objective status of the set of all natural numbers. It is difficult to believe, therefore, that a radical constructivist lets himself be influenced by the current literature on bifurcated supertasks. This does not make that literature less interesting, as, in establishing unthought-of connections between computability and the structure of space-time, it enriches (as does the existing literature on supertasks in general) the set of consequences that can be derived from our most interesting physical theories.
Bibliography
- Allis, V. and Koetsier, T., 1991, ‘On Some Paradoxes of the Infinite’, British Journal for the Philosophy of Science, 42, pp. 187–194
- Allis, V. and Koetsier, T., 1995, ‘On Some Paradoxes of the Infinite II’, British Journal for the Philosophy of Science, 46, pp. 235–247
- Alper, J.S. and Bridger, M., 1998, ‘Newtonian Supertasks: A Critical Analysis’ Synthese, 114, pp. 355–369
- Alper, J.S., Bridger, M., Earman , J. and Norton , J.D., 2000, ‘What is a Newtonian System? The Failure of Energy Conservation and Determinism in Supertasks’ Synthese, 124, pp.281–293
- Aristotle, Physics, (W. Charlton, trans.), Oxford: Oxford University Press, 1970
- Atkinson, D., 2007, ‘Losing Energy in Classical, Relativistic, and Quantum Mechanics’, Studies in History and Philosophy of Modern Physics, 38, pp. 170–180
- Atkinson, D., 2008, ‘A Relativistic Zeno Effect’, Synthese, 160, pp. 77–86
- Atkinson, D. and Johnson, P., (forthcoming), ‘Nonconservation of Energy and Loss of Determinism. I. Infinitely many colliding balls’, Foundations of Physics. [Preprint available from the author]
- Benacerraf, P., 1962, ‘Tasks, Super-Tasks, and Modern Eleatics’, Journal of Philosophy, LIX, pp. 765–784; reprinted in Salmon [1970]
- Benacerraf, P. and Putnam, H., 1964, Introduction, Philosophy of Mathematics: Selected Readings, P. Benacerraf and H. Putnam (eds.), 2nd edition, Cambridge: Cambridge University Press, pp. 1–27
- Benardete, J.A., 1964, Infinity: An Essay in Metaphysics, Oxford: Clarendon Press
- Berresford, G. C., 1981, ‘A Note on Thomson's Lamp “Paradox”’, Analysis, 41, pp. 1–7
- Black, M., 1950–1, ‘Achilles and the Tortoise’, Analysis, XI, pp. 91–101; reprinted in Salmon [1970]
- Black, M., 1954, Problems of Analysis, Ithaca: Cornell University Press
- Black, R., 2002, ‘Solution to a small infinite puzzle’, Analysis, 62.4, pp. 345–346
- Bokulich, A., 2003, ‘Quantum measurement and supertasks’, International Studies in the Philosophy of Science, 17.2, pp. 127–136
- Bostock, D., 1972–73, ‘Aristotle, Zeno and the Potential Infinite’, Proceedings of the Aristotelian Society, 73, pp. 37–51
- Burke, M.B., 1984, ‘The Infinitistic Thesis’, The Southern Journal of Philosophy, 22, pp. 295–305
- Burke, M.B., 2000a, ‘The Impossibility of Superfeats’, The Southern Journal of Philosophy, XXXVIII, pp.207–220
- Burke, M.B., 2000b, ‘The Staccato Run: a Contemporary Issue in the Zenonian Tradition’, The Modern Schoolman, LXXVIII, pp.1–8
- Bridger, M., and Alper, J. S., 1999, ‘On the Dynamics of Perez-Laraudogoitia's Supertask’, Synthese, 119, pp. 325–337
- Chihara, C., 1965, ‘On the Possibility of Completing an Infinite Task’, Philosophical Review, LXXIV, pp. 74–87
- Clark, P., and Read, S., 1984, ‘Hypertasks’, Synthese, 61, pp. 387–390
- Cooke, M.C., 2003, ‘Infinite Sequences: Finitist Consequence’, British Journal for the Philosophy of Science, 54, pp. 591–599
- Cotogno, P., 2003, ‘Hypercomputation and the Physical Church-Turing Thesis’, British Journal for the Philosophy of Science, 54 , pp. 181–223
- Davies, E.B., 2001, ‘Building Infinite Machines’, British Journal for the Philosophy of Science, 52 , pp. 671–682
- Earman, J., 1986, A Primer on Determinism, Dordrecht: Reidel
- Earman, J., 1994, Bangs, Crunches, Shrieks, and Whimpers: Singularities and Acausalities in Relativistic Spacetimes, New York: Oxford University Press
- Earman, J., and Norton, J.D., 1993, ‘Forever Is a Day: Supertasks in Pitowsky and Malament-Hogarth Spacetimes’, Philosophy of Science, 60, pp. 22–42
- Earman, J., and Norton, J. D., 1996, ‘Infinite Pains: The Trouble with Supertasks’, in Benacerraf and His Critics, A. Morton and S. Stich (eds.), Oxford: Blackwell, pp. 231–261
- Earman, J., and Norton, J. D., 1998, ‘Comments on Laraudogoitia's “Classical Particle Dynamics, Indeterminism and a Supertask”’, British Journal for the Philosophy of Science, 49, pp. 123–133
- Faris, J. A., 1996, The Paradoxes of Zeno, Aldershot: Avebury
- Forrest, P., 1999, ‘Supertasks and material objects’, Logique et Analyse, 166–167, pp. 441–446
- Friedman, K.S., 2002, ‘A small infinite puzzle’, Analysis, 62.4, pp. 344–345
- Gale, R. M. (ed.), 1968, The Philosophy of Time, London: MacMillan
- Glazebrook, T., 2001, ‘Zeno Against Mathematical Physics’, Journal of the History of Ideas, 62, pp.193–210
- Groarke, L., 1982, ‘Zeno's Dichotomy: Undermining the Modern Response’, Auslegung, 9, pp. 67–75
- Grünbaum, A. 1950–52 ‘Messrs. Black and Taylor on Temporal Paradoxes’, Analysis, 11–12, pp. 144–148
- Grünbaum, A., 1967, Modern Science and Zeno's Paradoxes, Middletown, CT: Wesleyan University Press
- Grünbaum, A., 1968, ‘Are “Infinity Machines” Paradoxical?’, Science, CLIX, pp. 396–406
- Grünbaum, A., 1969, ‘Can an Infinitude of Operations be Performed in a Finite Time?’, British Journal for the Philosophy of Science, 20, pp. 203–218
- Grünbaum, A., 1970, ‘Modern Science and Zeno's Paradoxes of Motion’, in Salmon [1970], pp. 200–250
- Hawthorne, J., 2000, “Before-Effect and Zeno Causality”, Nous, 34.4, pp. 622–633
- Hogarth, M. L., 1992, ‘Does General Relativity Allow an Observer to View an Eternity in a Finite Time?’, Foundations of Physics Letters, 5, pp. 173–181
- Hogarth, M. L., 1994, ‘Non-Turing Computers and Non-Turing Computability’, in PSA 1994, D. Hull, M. Forbes and R.M. Burian (eds.), 1, East Lansing: Philosophy of Science Association, pp. 126–138
- Holgate, P., 1994, ‘Discussion: Mathematical Notes on Ross's Paradox’, British Journal for the Philosophy of Science, 45, pp. 302–304
- Koetsier, T. and Allis, V., 1997, ‘Assaying Supertasks’, Logique & Analyse, 159, pp. 291–313
- McLaughlin, W. I., 1998, ‘Thomson's Lamp is Dysfunctional’, Synthese, 116, pp. 281–301
- Moore, A. W., 1989–90, ‘A Problem for Intuitionism: The Apparent Possibility of Performing Infinitely Many Tasks in a Finite Time’, Proceedings of the Aristotelian Society, 90, pp. 17–34
- Moore, A. W., 1990, The Infinite, London: Routledge
- Norton, J. D., 1999, ‘A Quantum Mechanical Supertask’, Foundations of Physics, 29, pp. 1265–1302
- Oppy, G., 2006, Philosophical Perspectives on Infinity, Cambridge: Cambridge University Press
- Owen, G. E. L., 1957–58, ‘Zeno and the Mathematicians’, Proceedings of the Aristotelian Society, LVIII, pp. 199–222, reprinted in Salmon [1970]
- Parsons, J., 2004, ‘The Eleatic hangover cure’, Analysis, 64, pp. 364–366
- Parsons, J., 2006, ‘Topological drinking problems’, Analysis, 66, pp. 149–154
- Peijnenburg, J. and Atkinson, D., 2008, ‘Achilles, the Tortoise and Colliding Balls’, History of Philosophy Quarterly, 25, pp. 187–201
- Peijnenburg, J. and Atkinson, D., forthcoming, ‘Lamps, cubes, balls and walls: Zeno problems and solutions’, Philosophical Studies, [Available online]
- Pérez Laraudogoitia, J., 1996, ‘A Beautiful Supertask’, Mind, 105, pp. 81–83
- Pérez Laraudogoitia, J., 1997, ‘Classical Particle Dynamics, Indeterminism and a Supertask’, British Journal for the Philosophy of Science, 48, pp. 49–54
- Pérez Laraudogoitia, J., 1998, ‘Infinity Machines and Creation Ex Nihilo’, Synthese, 115, pp. 259–265
- Pérez Laraudogoitia, J., 2001, ‘Indeterminism, classical gravitation and non-collision singularities’, International Studies in the Philosophy of Science, 15.3, pp. 269–274
- Pérez Laraudogoitia, J., 2005, ‘An Interesting Fallacy Concerning Dynamical Supertasks’, British Journal for the Philosophy of Science, 56, pp.321–334
- Pérez Laraudogoitia, J., 2006a, ‘A Look at the Staccato Run’, Synthese, 148, pp.433–441
- Pérez Laraudogoitia, J., 2006b, ‘Global Interaction in Classical Mechanics’, International Studies in the Philosophy of Science, 20, pp.173–183
- Pérez Laraudogoitia, J., 2007a, ‘Avoiding Infinite Masses’, Synthese, 156, pp.21–31
- Pérez Laraudogoitia, J., 2007b, ‘Supertasks, dynamical attractors and indeterminism’, Studies in History and Philosophy of Modern Physics, 38, pp.724–731
- Pérez Laraudogoitia, J., 2009a, ‘On Energy Conservation in Infinite Systems’, in Energy Conservation: New Research, G. Spadoni (ed.), New York: Nova Science Publishers, pp. 3–12
- Pérez Laraudogoitia, J., 2009b, ‘Physical Action Without Interaction’, Erkenntnis, 70, pp.365–377
- Pérez Laraudogoitia, J., forthcoming, ‘The Inverse Spaceship Paradox’, Synthese, [Available online]
- Pitowsky, I., 1990, ‘The Physical Church Thesis and Physical Computational Complexity’, Iyyun, 39, pp. 81–99
- Priest, G., 1982, ‘To Be and Not to Be: Dialectical Tense Logic’, Studia Logica, XLI, pp. 157–176
- Ray, C., 1990, ‘Paradoxical Tasks’, Analysis, 50, pp. 71–74
- Ray, C., 1991, Time, Space and Philosophy, London: Routledge
- Sainsbury, R. M., 1988, Paradoxes, Cambridge: Cambridge University Press
- Salmon, W., (ed.), 1970, Zeno's Paradoxes, Indianapolis: Bobbs-Merril
- Salmon, W., 1980, Space, Time and Motion: A Philosophical Introduction, Minneapolis: University of Minnesota Press
- Smith, J. W., 1986, Reason, Science and Paradox, London: Croom Helm
- Sorabji, R., 1983, Time, Creation and the Continuum, London: Gerald Duckworth and Co. Ltd.
- Svozil, K., 1993, Randomness and Undecidability in Physics, Singapore: World Scientific
- Taylor, R., 1951–52, ‘Mr. Black on Temporal Paradoxes’, Analysis, XII, pp. 38–44
- Taylor, R., 1952–53, ‘Mr. Wisdom on Temporal Paradoxes’, Analysis, XIII, pp. 15–17
- Thomson, J., 1954–55, ‘Tasks and Super-Tasks’, Analysis, XV, pp. 1–13; reprinted in Salmon [1970]
- Thomson, J., 1967, ‘Infinity in Mathematics and Logic’, in Encyclopedia of Philosophy, P. Edwards (ed.), 4, New York: MacMillan, pp. 183–90
- Thomson, J., 1970, ‘Comments on Professor Benacerraf's Paper’, in Salmon [1970], pp. 130–38.
- Van Bendegem, J. P., 1994, ‘Ross' Paradox is an Impossible Super Task’, British Journal for the Philosophy of Science, 45, pp. 743–48
- Van Bendegem, J. P., 1995–1997, ‘In Defence of Discrete Space and Time’, Logique & Analyse, 150–151–152, pp. 127–150
- Vlastos, G., 1966, ‘Zeno's Race Course’, Journal of the History of Philosophy, IV, pp. 95–108
- Vlastos, G., 1967, ‘Zeno of Elea’, in Encyclopedia of Philosophy, P. Edwards (ed.), 8, New York: MacMillan, pp.369–79
- Watling, J., 1953, ‘The Sum of an Infinite Series’, Analysis, XIII, pp. 39–46
- Wedeking, G. A., 1968, ‘On a Finitist “Solution” to Some Zenonian Paradoxes’, Mind, 77, pp. 420–26
- Weyl, H., 1949, Philosophy of Mathematics and Natural Science, Princeton: Princeton University Press
- Whitrow, G. J., 1961, The Natural Philosophy of Time, Edinburgh: Thomas Nelson & Sons
- Wisdom, J. O., 1951–52, ‘Achilles on a Physical Racecourse’, Analysis, XII, pp. 67–72, reprinted in Salmon [1970]
Other Internet Resources
[Please contact the author with suggestions.]
Related Entries
determinism: causal | infinity | space and time: Malament-Hogarth spacetimes and the new computability | Zeno of Elea: Zeno's paradoxes

