Church's Type Theory
Church's type theory is a formal logical language which includes first-order logic, but is more expressive in a practical sense. It is used, with some modifications and enhancements, in most modern applications of type theory. It is particularly well suited to the formalization of mathematics and other disciplines and to specifying and verifying hardware and software. A great wealth of technical knowledge can be expressed very naturally in it. With possible enhancements, Church's type theory constitutes an excellent formal language for representing the knowledge in automated information systems, sophisticated automated reasoning systems, systems for verifying the correctness of mathematical proofs, and certain projects involving logic and artificial intelligence. Some examples are given in Section 1.2.2 below.
Type theories are also called higher-order logics, since they allow quantification not only over individual variables (as in first-order logic), but also over function, predicate, and even higher order variables. Type theories characteristically assign types to entities, distinguishing, for example, between numbers, set of numbers, functions from numbers to sets of numbers, and sets of such functions. As illustrated in Section 1.2.2 below, these distinctions allow one to discuss the conceptually rich world of sets and functions without encountering the paradoxes of naive set theory.
Church's type theory is a formulation of type theory that was introduced by Alonzo Church in Church 1940. In certain respects, it is simpler and more general than the type theory introduced by Bertrand Russell in Russell 1908 and Whitehead & Russell 1927a. Since properties and relations can be regarded as functions from entities to truth values, the concept of a function is taken as primitive in Church's type theory, and the λ-notation which Church introduced in Church 1932 and Church 1941 is incorporated into the formal language.
- 1. Syntax
- 2. Semantics
- 3. Metatheory
- 4. Automation
- Bibliography
- Other Internet Resources
- Related Entries
1. Syntax
1.1 Fundamental Ideas
We start with an informal description of the fundamental ideas underlying the syntax of Church's formulation of type theory.
All entities have types, and if α and β are types, the type of functions from elements of type β to elements of type α is written as (αβ). (This notation was introduced by Church, but some authors write (β → α) instead of (αβ). See, for example, Section 4 of the entry on type theory.)
As noted by Schonfinkel (1924), functions of more than one argument can be represented in terms of functions of one argument when the values of these functions can themselves be functions. For example, if f is a function of two arguments, for each element x of the left domain of f there is a function g (depending on x) such that gy = fxy for each element y of the right domain of f. We may now write g = fx, and regard f as a function of a single argument, whose value for any argument x in its domain is a function fx, whose value for any argument y in its domain is fxy.
For a more explicit example, consider the function + which carries any pair of natural numbers to their sum. We may denote this function by +((σσ)σ), where σ is the type of natural numbers. Given any number x, [+((σσ)σ)x] is the function which, when applied to any number y, gives the value [[+((σσ)σ)x]y], which is ordinarily abbreviated as x + y. Thus [+((σσ)σ)x] is the function of one argument which adds x to any number. When we think of +((σσ)σ) as a function of one argument, we see that it maps any number x to the function [+((σσ)σ)x].
More generally, if f is a function which maps n-tuples ⟨wβ, xγ, …, yδ, zτ⟩ of elements of types β,γ,…,δ,τ, respectively, to elements of type α, we may assign to f the type ((…((ατ)δ)…γ)β). It is customary to use the convention of association to the left to omit parentheses, and write this type symbol simply as (ατδ…γβ).
A set or property can be represented by a function which maps elements to truth values, so that an element is in the set, or has the property, in question iff the function representing the set or property maps that element to truth. When a statement is asserted, the speaker means that it is true, so that sx means that sx is true, which also expresses the assertions that s maps x to truth and that x ∈ s. In other words, x ∈ s iff sx. We take ο as the type symbol denoting the type of truth values, so we may speak of any function of type (οα) as a set of elements of type α. A function of type ((οα)β) is a binary relation between elements of type β and elements of type α. For example, if σ is the type of the natural numbers, and < is the order relation between natural numbers, < has type (οσσ), and for all natural numbers x and y, <xy (which we ordinarily write as x<y) has the value truth iff x is less than y. Of course, < can also be regarded as the function which maps each natural number x to the set <x of all natural numbers y such that x is less than y. Thus sets, properties, and relations may be regarded as particular kinds of functions.
Expressions which denote elements of type α are called wffs of type α. Thus, statements of type theory are wffs of type ο.
If Aα is a wff of type α in which uαβ is not free, the function uαβ such that ∀vβ[uαβvβ = Aα] is denoted by [λvβ Aα]. Thus λvβ is a variable-binder, like ∀vβ or ∃vβ (but with a quite different meaning, of course); λ is known as an abstraction operator. [λvβ Aα] denotes the function whose value on any argument vβ is Aα, where vβ may occur free in Aα. For example, [λnσ [4·nσ+3]] denotes the function whose value on any natural number n is 4·n + 3. Hence when we apply this function to the number 5 we obtain [λnσ [4·nσ+3]]5 = 4·5 + 3 = 23.
We use Sub(B,v,A) as a notation for the result of substituting B for v in A, and SubFree(B,v,A) as a notation for the result of substituting B for all free occurrences of v in A. The process of replacing [λvβ Aα]Bβ by SubFree(Bβ,vβ,Aα) (or vice-versa) is known as β-conversion, which is one form of λ-conversion. Of course, when Aο is a wff of type ο, [λvβ Aο] denotes the set of all elements vβ (of type β) of which Aο is true; this set may also be denoted by {vβ | Aο}. For example, [λx x<y] denotes the set of x such that x is less than y (as well as that property which a number x has it if is less than y. In familiar set-theoretic notation, [λvβ Aο]Bβ = SubFree(Bβ,vβ,Aο) would be written Bβ ∈ {vβ | Aο} ≡ SubFree(Bβ,vβ,Aο). (By the Axiom of Extensionality for truth values, when Cο and Dο are of type ο, Cο ≡ Dο is equivalent to Cο = Dο.)
Propositional connectives and quantifiers can be assigned types and can be denoted by constants of these types. The negation function maps truth values to truth values, so it has type (οο). Similarly, disjunction and conjunction (etc.) are binary functions from truth values to truth values, so they have type (οοο).
The statement ∀xαAο is true iff the set [λxα Aο] contains all elements of type α. A constant Πο(οα) can be introduced (for each type symbol α) to denote a property of sets: a set sοα has the property Πο(οα) iff sοα contains all elements of type α. With this interpretation
∀sοα[Πο(οα)sοα ≡ ∀xα[sοαxα]]
should be true, as well as
Πο(οα)[λxα Aο] ≡ ∀xα[[λxα Aο]xα] (*)
for any wff Aο and variable xα. Since by λ-conversion we have
[λxα Aο]xα ≡ Aο
equation (*) can be written more simply as
Πο(οα)[λxα Aο] ≡ ∀xαAο.
Thus, ∀xα can be defined in terms of Πο(οα), and λ is the only variable-binder that is needed.
1.2 Formulas
1.2.1 Definitions
Type symbols are defined inductively as follows:
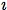 is a type symbol (denoting the type of individuals). There
may also be additional primitive type symbols which are used in
formalizing disciplines where it is natural to have several sorts of
individuals. [Editors Note: In what follows, the entry distinguishes
between the symbols
is a type symbol (denoting the type of individuals). There
may also be additional primitive type symbols which are used in
formalizing disciplines where it is natural to have several sorts of
individuals. [Editors Note: In what follows, the entry distinguishes
between the symbols
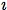 ,
ι, and
,
ι, and
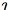 . The first is the
symbol used for the type of individuals; the second is the symbol
used for a logical constant (see below); the third is the symbol used as
a variable-binding operator that represents the definite
description "the". The reader should check to see that the
browser is displaying these symbols correctly.]
. The first is the
symbol used for the type of individuals; the second is the symbol
used for a logical constant (see below); the third is the symbol used as
a variable-binding operator that represents the definite
description "the". The reader should check to see that the
browser is displaying these symbols correctly.]
- ο is a type symbol (denoting the type of truth values).
- If α and β are type symbols, then (αβ) is a type symbol (denoting the type of functions from elements of type β to elements of type α).
The primitive symbols are the following:
- Improper symbols: [, ], λ
- For each type symbol α, a denumerable list of variables of type α: aα, bα, cα …
- Logical constants: ∼(οο), ∨((οο)ο), Π(ο(οα)), ι(α(οα)) (for each type symbol α). [The types of these constants are indicated by their subscripts.] The symbol ∼(οο) denotes negation, ∨((οο)ο) denotes disjunction, and Π(ο(οα)) is used in defining the universal quantifier as discussed above. ι(α(οα)) serves either as a description or selection operator as discussed in Section 1.3.4 and Section 1.3.5 below.
- In addition, there may be other constants of various types, which will be called nonlogical constants or parameters. Each choice of parameters determines a particular formulation of the system of type theory. Parameters are typically used as names for particular entities in the discipline being formalized.
Before we state the definition of a "formula", a word of caution is in order. The reader may be accustomed to thinking of a formula as an expression which plays the role of an assertion in a formal language, and of a term as an expression which designates an object. Church's terminology is somewhat different, and provides a uniform way of discussing expressions of many different types.
A formula is a finite sequence of primitive symbols. Certain formulas are called well-formed formulas (wffs). We write wffα as an abbreviation for wff of type α, and define this concept inductively as follows:
- A primitive variable or constant of type α is a wffα.
- If Aαβ and Bβ are wffs of the indicated types, then [Aαβ Bβ] is a wffα.
- If xβ is a variable of type β and Aα is a wff, then [λxβ Aα] is a wff(αβ).
Note, for example, that by (a) ∼(οο) is a wff(οο), so by (b) if Aο is a wffο, then [∼(οο) Aο] is a wffο. Usually, the latter wff will simply be written as ∼A.
Definitions and abbreviations:
- [Aο ∨ Bο] stands for [[∨((oo)o) Aο] Bο].
- [Aο ⊃ Bο] stands for [[∼(οο) Aο] ∨ Bο].
- [∀xαAο] stands for [Π(ο(οα)) [λxα Aο]].
- Other propositional connectives, and the existential quantifier, are defined in familiar ways. In particular,
[Aο ≡ Bο] stands for [[Aο ⊃ Bο] ∧ [Bο ⊃ Aο]].- Qοαα stands for [λxαλyα ∀f(οα)[f(οα)xα ⊃ f(οα)yα]].
- [Aα = Bα] stands for QοααAαBα.
The last definition is known as the Leibnizian definition of equality. It asserts that x and y are the same if y has every property that x has. Actually, Leibniz called his definition "the identity of indiscernibles" and gave it in the form of a biconditional: x and y are the same if x and y have exactly the same properties. It is not difficult to show that these two forms of the definition are logically equivalent.
1.2.2 Examples
We now provide a few examples to illustrate how various assertions and concepts can be expressed in Church's type theory. It is often convenient to omit type symbols from some or all occurrences of variables and constants, and use conventions for omitting parentheses and brackets, but this is mostly avoided here. However, in writing type symbols we often omit outer parentheses and use the convention of association to the left; thus οι ι is an abbreviation for ((οι)ι).
Example 1
To express the assertion that Napoleon is charismatic we introduce
constants
Charismaticο and
Napoleon
and
Napoleon ,
with the types indicated by their subscripts and the obvious
meanings, and assert the wff
,
with the types indicated by their subscripts and the obvious
meanings, and assert the wff
CharismaticοNapoleon
If we wish to express the assertion that “Napoleon has all the
properties of a great general”, we might consider interpreting
this to mean that “Napoleon has all the properties of some great
general”, but it seems more appropriate to interpret this
statement as meaning that “Napoleon has all the properties which
all great generals have”. If the constant
GreatGeneralο is added to the formal language, this can be expressed by the wff
is added to the formal language, this can be expressed by the wff
∀pο[∀g
[GreatGeneralο
g
⊃ pο
g
] ⊃ pο
Napoleon
].
As an example of such a property, we note that the sentence “Napoleon's soldiers admire him” can be expressed in a similar way by the wff
∀x[Soldierο
x
∧ [CommanderOf
x
= Napoleon
] ⊃
Admiresοx
Napoleon
].
By λ-conversion, this is equivalent to
[λn
∀x
[Soldierο
x
∧ [CommanderOf
x
= n
] ⊃ Admiresο
x
n
]]Napoleon
.
This statement asserts that one of the properties which Napoleon has is that of being admired by his soldiers. The property itself is expressed by the wff
[λn∀x
[Soldierο
x
∧ [CommanderOf
x
= n
] ⊃ Admiresο
x
n
]].
Example 2
We illustrate some potential applications of type theory with the following fable.
A rich and somewhat eccentric lady named Sheila has an ostrich and a cheetah as pets, and she wishes to take them from her hotel to her remote and almost inaccessible farm. Various portions of the trip may involve using elevators, boxcars, airplanes, trucks, very small boats, donkey carts, suspension bridges, etc., and she and the pets will not always be together. She knows that she must not permit the ostrich and the cheetah to be together when she is not with them. We consider how certain aspects of this problem can be formalized so that Sheila can use an automated reasoning system to help analyze the possibilities.
There will be a set Moments of instants or intervals of time during the trip. She will start the trip at the location Hotel and moment Start, and end it at the location Farm and moment Finish. Moments will have type τ, and locations will have type ρ. A state will have type σ and will specify the location of Sheila, the ostrich, and the cheetah at a given moment. A plan will specify where the entities will be at each moment according to this plan. It will be a function from moments to states, and will have type (στ). The exact representation of states need not concern us, but there will be functions from states to locations called LocationOfSheila, LocationOfOstrich, and LocationOfCheetah which provide the indicated information. Thus, LocationOfSheilaρσ[pστ tτ] will be the location of Sheila according to plan pστ at moment tτ. The set Proposalsο(στ) is the set of plans Sheila is considering.
We define a plan p to be acceptable if, according to that plan, the group starts at the hotel, finishes at the farm, and whenever the ostrich and the cheetah are together, Sheila is there too. Formally, we define Acceptableο(στ) as
[λpστ [LocationOfSheilaρσ [pστ Startτ] = Hotelρ ∧ LocationOfOstrichρσ[pστ Startτ] = Hotelρ ∧ LocationOfCheetahρσ[pστ Startτ] = Hotelρ ∧ LocationOfSheilaρσ[pστ Finishτ] = Farmρ ∧ LocationOfOstrichρσ[pστ Finishτ] = Farmρ ∧ LocationOfCheetahρσ[pστ Finishτ] = Farmρ ∧ ∀tτ[Momentsοτ tτ ⊃ [[LocationOfOstrichρσ[pστ tτ] = LocationOfCheetahρσ[pστ tτ]] ⊃ [LocationOfSheilaρσ[pστ tτ] = LocationOfCheetahρσ[pστ tτ] ] ] ] ] ].
We can express the assertion that Sheila has a way to accomplish her objective with the formula
∃pστ[Proposalsο(στ)pστ ∧ Acceptableο(στ)pστ].
Example 3
We now provide a mathematical example. Mathematical ideas can be
expressed in type theory without introducing any new constants. An
iterate of a function f which maps a set to itself
is a function which applies f one or more times. For example,
if g(x) =
f(f(f(x))), then g is an
iterate of f.
[ITERATE+ο(
 )(
)(
 ) f
) f
 g
g
 ]
means that
g
]
means that
g
 is an iterate of
f
is an iterate of
f
 .
ITERATE+ο(
.
ITERATE+ο(
 )(
)(
 )
is defined (inductively) as
)
is defined (inductively) as
λfλg
∀pο(
)[pο(
)f
∧ ∀j
[pο(
)j
⊃ pο(
)[λx
f
[j
x
]]] ⊃ pο(
)g
].
Thus, g is an iterate of f if g is in every
set p of functions which contains f and which
contains the function [λx f
f
 [j
[j
 x
x ]]
(i.e., f composed with j) whenever it contains
j.
]]
(i.e., f composed with j) whenever it contains
j.
A fixed point of f is an element y such that f(y) = y.
It can be proved that if some iterate of a function f has a unique fixed point, then f itself has a fixed point. This theorem can be expressed by the wff
∀f[∃g
[ITERATE+ο(
)(
) f
g
∧ ∃x
[g
x
= x
∧ ∀z
[g
z
= z
⊃ z
= x
] ] ] ⊃
∃y[f
y
= y
] ].
See Andrews et al. 1996, for a discussion of how this theorem, which is called THM15B, can be proved automatically.
Example 4
Suppose we omit the use of type symbols in the definitions of wffs. Then we can write the formula [λx ∼x x], which we shall call R. It can be regarded as denoting the set of all sets x such that x is not in x. We may then consider the formula [R R], which expresses the assertion that R is in itself. We can clearly prove [R R] ≡ [λx ∼x x]R, so by λ-conversion we can derive [R R] ≡ ∼[R R], which is a contradiction. This is Russell's paradox. Russell's discovery of this paradox (Russell 1903, 101-107) played a crucial role in the development of type theory. Of course, when type symbols are present, R is not well-formed, and the contradiction cannot be derived.
1.3 Axioms and Rules of Inference
1.3.1 Rules of Inference
- Alphabetic Change of Bound Variables (α-conversion). To replace any well-formed part [λxβ Aα] of a wff by [λyβ Sub(yβ,xβ,Aα)], provided that yβ does not occur in Aα and xβ is not bound in Aα.
- β-contraction. To replace any well-formed part [[λxα Bβ] Aα] of a wff by Sub(Aα,xα,Bβ), provided that the bound variables of Bβ are distinct both from xα and from the free variables of Aα.
- β-expansion. To infer C from D if D can be inferred from C by a single application of β-contraction.
- Substitution. From F(οα)xα, to infer F(οα)Aα, provided that xα is not a free variable of F(οα).
- Modus Ponens. From [Aο ⊃ Bο] and Aο, to infer Bο.
- Generalization. From F(οα)xα to infer Πο(οα)F(οα), provided that xα is not a free variable of F(οα).
1.3.2 Elementary Type Theory
We start by listing the axioms for what we shall call elementary type theory.
| (1) | [pο ∨ pο] ⊃ pο |
| (2) | pο ⊃ [pο ∨ qο] |
| (3) | [pο ∨ qο] ⊃ [qο ∨ pο] |
| (4) | [pο ⊃ qο] ⊃ [[rο ∨ pο] ⊃ [rο ∨ qο] ] |
| (5α) | Πο(οα) f(οα) ⊃ f(οα) xα |
| (6α) | ∀xα[pο ∨ f(οα)xα] ⊃ [pο ∨ Πο(οα) f(οα)] |
The theorems of elementary type theory are those theorems which can be derived from Axioms 1–6α (for all type symbols α). We shall sometimes refer to elementary type theory as T . It embodies the logic of propositional connectives, quantifiers, and λ-conversion in the context of type theory.
To illustrate the rules and axioms introduced above, we give a short and trivial proof in T . (The proof is actually quite inefficient, since line 3 is not used later, and line 7 can be derived directly from line 5 without using line 6.) Following each wff of the proof, we indicate how it was inferred.[1]
| 1. | ∀x [pο
∨
fο [pο
∨
fο x x ]
⊃ [pο
∨
Πο(ο ]
⊃ [pο
∨
Πο(ο )
fο )
fο ] ] |
Axiom 6 |
| 2. | [λfο [∀x [∀x [pο
∨
fο [pο
∨
fο x x ]
⊃
[pο
∨
Πο(ο ]
⊃
[pο
∨
Πο(ο ) fο ) fο ] ] ]fο ] ] ]fο |
β-expansion: 1 |
| 3. | Πο(ο(ο ))[λfο ))[λfο [∀x [∀x [pο
∨
fο [pο
∨
fο x x ]
⊃
[pο
∨
Πο(ο ]
⊃
[pο
∨
Πο(ο )fο )fο ] ] ] ] ] ] |
Generalization: 2 |
| 4. | [λfο [∀x [∀x [pο∨fο [pο∨fο x x ]
⊃
[pο ∨
Πο(ο ]
⊃
[pο ∨
Πο(ο )fο )fο ] ] ] [λx ] ] ] [λx rο rο x x ] ] |
Substitution: 2 |
| 5. | ∀x [pο
∨
[λx [pο
∨
[λx rο rο x x ]x ]x ]
⊃
[pο
∨
Πο(ο ]
⊃
[pο
∨
Πο(ο )[λx )[λx rο rο x x ] ] ] ] |
β-contraction: 4 |
| 6. | ∀x [pο
∨
[λy [pο
∨
[λy rο rο y y ]x ]x ]
⊃
[pο
∨
Πο(ο ]
⊃
[pο
∨
Πο(ο )[λx )[λx rο rο x x ] ] ] ] |
α-conversion: 5 |
| 7. | ∀x [pο
∨
rο [pο
∨
rο x x ]
⊃
[pο
∨
Πο(ο ]
⊃
[pο
∨
Πο(ο )[λx )[λx rο rο x x ] ] ] ] |
β-contraction: 6 |
Note that (3) can be written as
(3′) ∀fο[∀x
[pο ∨ fο
x
] ⊃ [pο ∨ Πο(ο
)fο
] ]
and (7) can be written as
(7′) ∀x[pο ∨ rο
x
] ⊃ [pο ∨ ∀x
rο
x
]
We have thus derived a well known law of quantification theory. We
illustrate one possible interpretation of the wff (7′) (which is
closely related to Axiom 6) by considering a situation in which a
rancher puts some horses in a corral and leaves for the night. Later,
he cannot remember whether he closed the gate to the corral. While
reflecting on the situation, he comes to a conclusion which can be
expressed by (7′) if we take the horses to be the elements of
type
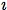 ,
interpret pο to mean "the gate was closed",
and interpret
rο
,
interpret pο to mean "the gate was closed",
and interpret
rο so that rο
so that rο x
x asserts
"x
asserts
"x left the corral". With this interpretation, (7′) says "If it is
true of every horse that the gate was closed or that horse left the
corral, then the gate was closed or every horse left the corral."
left the corral". With this interpretation, (7′) says "If it is
true of every horse that the gate was closed or that horse left the
corral, then the gate was closed or every horse left the corral."
To the axioms listed above we add the axioms below to obtain Church's type theory.
1.3.3 Axioms of Extensionality
| (7ο) | [xο ≡ yο] ⊃ xο = yο |
| (7αβ) | ∀xβ[fαβ xβ = gαβ xβ] ⊃ fαβ = gαβ |
Church did not include Axiom 7ο in his list of axioms in Church 1940, but he mentioned the possibility of including it. Henkin did include it in Henkin 1950.
1.3.4 Descriptions
The expression
∃1xαAο
stands for
[λpοα ∃yα[pοα yα ∧ ∀zα[pοα zα ⊃ zα = yα] ] [λxα Aο].
For example,
∃1xαPοαxα
stands for
[λpοα ∃yα[pοα yα ∧ ∀zα[pοα zα ⊃ zα = yα] ] [λxα Pοαxα].
By λ-conversion, this is equivalent to:
∃yα[[λxα Pοαxα]yα ∧ ∀zα[[λxα Pοαxα]zα ⊃ zα = yα] ]
which reduces by λ-conversion to:
∃yα[Pοαyα ∧ ∀zα[Pοαzα ⊃ zα = yα] ]
This asserts that there is a unique element which has the property Pοα. From this example we can see that in general, ∃1xα Aο expresses the assertion that "there is a unique xα such that Aο".
When there is a unique such element xα,
it is convenient to have the notation
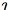 xαAο to represent the
expression "the xα such that
Aο". Russell showed
in Whitehead & Russell 1927b
how to provide contextual definitions for such notations
in his formulation of type theory. In Church's type theory
xαAο to represent the
expression "the xα such that
Aο". Russell showed
in Whitehead & Russell 1927b
how to provide contextual definitions for such notations
in his formulation of type theory. In Church's type theory
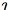 xαAο
is defined as
ια(οα)[λxα Aο].
Thus,
xαAο
is defined as
ια(οα)[λxα Aο].
Thus, 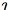 behaves like
a variable-binding operator, but it is defined in terms of λ
with the aid of the constant
ια(οα). Thus, λ is still
the only variable-binding operator that is needed.
behaves like
a variable-binding operator, but it is defined in terms of λ
with the aid of the constant
ια(οα). Thus, λ is still
the only variable-binding operator that is needed.
Since Aο describes xα, ια(οα) is called a description operator. Associated with this notation is the following:
Axiom of Descriptions:
(8α) ∃1xα[pοαxα] ⊃ pοα [ια(οα) pοα]
This says that when the set pοα has a unique member, then ια(οα)pοα is in pοα, and therefore is that unique member. Thus, this axiom asserts that ια(οα) maps one-element sets to their unique members.
If from certain hypotheses one can prove ∃1xαAο, then by using Axiom 8α one can derive
[λxαAο][ια(οα)[λxαAο] ],
which can also be written as
[λxαAο](xα)Aο.
We illustrate the usefulness of the description operator with a small example. Suppose we have formalized the theory of real numbers, and our theory has constants 1ρ and ×ρρρ to represent the number 1 and the multiplication function, respectively. (Here ρ is the type of real numbers.) To represent the multiplicative inverse function, we can define the wff INVρρ as:
[λzρ(xρ)[×ρρρzρxρ = 1ρ]].
Of course, in traditional mathematical notation we would not write the type symbols, and we would write ×ρρρzρxρ as z × x and write INVρρz as z−1. Thus z−1 is defined to be that x such that z × x = 1. When Z is provably not 0, we will be able to prove ∃1xρ[×ρρρZ xρ = 1ρ] and Z × Z−1 = 1, but if we cannot establish that Z is not 0, nothing significant about Z−1 will be provable.
1.3.5 Axiom of Choice
The Axiom of Choice can be expressed as follows in Church's type theory:
(9α) ∃xα pοαxα ⊃ pοα[ια(οα) pοα]
(9α) says that the choice function
ια(οα) chooses from every nonempty set pοα
an element (which is designated as
ια(οα)pοα)
of that set. When this form of the Axiom of Choice is included
in the list of axioms, ια(οα)
is called a selection
operator[2]
instead of a description operator, and
(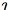 xα)Aο
means "an xα such that
Aο" when there is some such
element sα.
xα)Aο
means "an xα such that
Aο" when there is some such
element sα.
It is natural to call
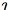 a definite description operator in contexts where
(
a definite description operator in contexts where
(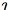 xα)Aο
means "the xα such that
Aο", and to call it an
indefinite description operator in contexts where
(
xα)Aο
means "the xα such that
Aο", and to call it an
indefinite description operator in contexts where
(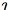 xα)Aο
means "an xα such that
Aο".
xα)Aο
means "an xα such that
Aο".
Clearly the Axiom of Choice implies the Axiom of Descriptions, but sometimes formulations of type theory are used which include the Axiom of Descriptions, but not the Axiom of Choice.
Another formulation of the Axiom of Choice simply asserts the existence of a choice function without explicitly naming it:
(ACα) ∃jα(οα) ∀pοα [∃xα pοαxα ⊃ pοα [jα(οα) pοα] ]
Normally when one assumes the Axiom of Choice in type theory, one assumes it as an axiom schema, and asserts ACα for each type symbol α.
Before proceeding, we need to introduce some terminology. Q0 is an alternative formulation of Church's type theory which will be described in Section 1.4 and is equivalent to the system described above using Axioms 1–8. A type symbol is propositional if the only symbols which occur in it are ο and parentheses.
Yasuhara (1975) defined the relation ‘≥’ between types as the reflexive transitive closure of the minimal relation such that (α β) ≥ α. and (α β) ≥ β. He established that:
- If α ≥ β, then Q0 ⊦ ACα ⊃ ACβ.
- Given a set S of types, none of which is propositional, there is a model of Q0 in which ACα fails if and only if α ≥ β for some β in S.
Büchi (1953) has shown that while the schemas expressing the Axiom of Choice and Zorn's Lemma can be derived from each other, the relationships between the particular types involved are complex.
1.3.6 Axioms of Infinity
One can define the natural numbers (and therefore other basic mathematical structures such as the real and complex numbers) in type theory, but to prove that they have the required properties (such as Peano's Postulates), one needs an Axiom of Infinity. There are many viable possibilities for such an axiom, such as those discussed in Church 1940.
1.4 A Formulation Based on Equality
In Section 1.2.1, ∼(οο), ∨((οο)ο), and the Π(ο(οα))'s were taken as primitive constants, and the wffs Qοαα which denote equality relations at type α were defined in terms of these. We now present an alternative formulation Q0 of Church's type theory in which there are primitive constants Qοαα detnoting equality, and ∼(οο), ∨((οο)ο), and the Π(ο(οα))'s are defined in terms of the Qοαα's.
Tarski (1923) noted that in the context of higher-order logic, one can define propositional connectives in terms of logical equivalence and quantifiers. Quine (1937) showed how to define quantifiers in terms of inclusion and abstraction. Henkin (1963) developed a formulation of Church's type theory based on equality in which he restricted attention to propositional types, and Andrews (1963) simplified the axioms for this system. Q0 is based on these ideas, and can be shown to be equivalent to a formulation of Church's type theory using Axioms 1–8 of the preceding sections. This section provides an alternative to the material in the preceding Sections 1.2.1 – 1.3.4.
- Type symbols, improper symbols, and variables are defined as in Section 1.2.1.
- Logical constants:
Q((οα)α),
and
ι(
 (ο
(ο )).
)). - Wffs are defined as in Section 1.2.1.
We employ the following definitions and abbreviations:
- [Aα = Bα] stands for [Qοαα Aα Bα]
- [Aο ≡ Bο] stands for [QοοοAο Bο]
- Tο stands for [Qοοο = Qοοο]
- Fο stands for [λxο Tο] = [λxο xο]
- Πο(οα) stands for [Qο(οα)(οα) [λxα Tο] ]
- [∀xα A] stands for [Πο(οα) [λxα A] ]
- ∧οοο stands for [λxολyο[[λgοοο[gοοοTοTο]] = [λgοοο[gοοοxοyο]]]]
- [Aο ∧ Bο] stands for [∧οοοAοBο]
- ∼οο stands for [QοοοFο]
Tο denotes truth. The meaning of Πο(οα) was discussed in Section 1.1. To see that this definition of Πο(οα) is appropriate, note that [λxαT] denotes the set of all elements of type α, and that Πο(οα)sοα stands for [Qο(οα)(οα)[λxαT]]sοα and for [λxαT] = sοα. Therefore Πο(οα)sοα asserts that sοα is the set of all elements of type α, so sοα contains all elements of type α. It can be seen that Fο can also be written as ∀xοxο, which asserts that everything is true. This is false, so Fο denotes falsehood. The expression [λgοοο[gοοοxοyο]] can be used to represent the ordered pair ⟨xο,yο⟩, and the conjunction xο ∧ yο is true iff xο and yο are both true, i.e., iff ⟨Tο,Tο⟩ = ⟨xο,yο⟩. Hence xο ∧ yο can be expressed by the formula [λgοοο[gοοοTοTο]] = [λgοοο[gοοοxοyο]].
Other propositional connectives and the existential quantifier are
easily defined. By using
ι( (ο
(ο )), one can define description
operators ια(οα)
for all types α.
)), one can define description
operators ια(οα)
for all types α.
Q0 has the following single rule of inference and axioms:
Rule R:
From C and Aα = Bα, to infer the result of replacing one occurrence of Aα in C by an occurrence of Bα, provided that the occurrence of Aα in C is not (an occurrence of a variable) immediately preceded by λ.Axioms for Q0:
(1) [gοοTο ∧ gοοFο] = ∀xο[gοοxο] (2α) [xα = yα] ⊃ [hοαxα = hοαyα] (3αβ) [fαβ = gαβ] = ∀xβ[fαβxβ = gαβxβ] (4) [λxαBβ]Aα = SubFree(Aα,xα,Bβ), provided that Aα is free for x in Bβ. (5) ι (ο
)[Qο
y
] = y
2. Semantics
It is natural to compare the semantics of type theory with the semantics of first-order logic, where the theorems are precisely the wffs which are valid in all interpretations. From an intuitive point of view, the natural interpretations of type theory are standard models, which are defined below. However, it is a consequence of Gödel's Incompleteness Theorem (Gödel 1931) that axioms 1–9 do not suffice to derive all wffs which are valid in all standard models, and there is no consistent recursively axiomatized extension of these axioms which suffices for this purpose. Nevertheless, experience shows that these axioms are sufficient for most purposes, and Leon Henkin considered the problem of clarifying in what sense they are complete. The definitions and theorem below constitute Henkin's (1950) solution to this problem.
A frame is a collection
{Dα}α
of nonempty domains (sets)
Dα,
one for each type symbol α, such that
Dο =
{T,F}
(where T represents truth and
F represents falsehood),
and
Dαβ
is some collection of functions mapping
Dβ
into
Dα.
The members of
D are called individuals.
are called individuals.
An interpretation ⟨{Dα}α, ℑ⟩ consists of a frame and a function ℑ which maps each constant C of type α to an appropriate element of Dα, which is called the denotation of C.
An assignment of values in the frame {Dα}α to variables is a function φ such that φxα ∈ Dα for each variable xα.
An interpretation M = ⟨{Dα}α, ℑ⟩ is a general model iff there is a binary function V such that VφAα ∈ Dα for each assignment φ and wff Aα, and the following conditions are satisfied for all assignments and all wffs:
- Vφxα = φxα for each variable xα.
- VφAα = ℑAα if Aα is a primitive constant.
- Vφ[AαβBβ] = (VφAαβ)(VφBβ) (the value of a function VφAαβ at the argument VφBβ).
- Vφ[λxαBβ] = that function from Dα into Dβ whose value for each argument z ∈ Dα is VψBβ, where ψ is that assignment such that ψxα = z and ψyβ = φyβ if yβ ≠ xα.
If an interpretation M is a general model, the function V is uniquely determined. VφAα is called the value of Aα in M with respect to φ.
An interpretation ⟨{Dα}α, ℑ⟩ is a standard model iff for all α and β, Dαβ is the set of all functions from Dβ into Dα. Clearly a standard model is a general model.
We say that a wff A is valid in a model M iff VφA = T for every assignment φ into M. A model for a set H of wffs is a model in which each wff of H is valid.
A wff A is valid in the general [standard] sense iff A is valid in every general [standard] model. Clearly a wff which is valid in the general sense is valid in the standard sense, but the converse of this statement is false.
Henkin's Completeness and Soundness Theorem.
A wff is a theorem if and only if it is valid in the general sense.
Not all frames belong to interpretations, and not all interpretations are general models. In order to be a general model, an interpretation must have a frame satisfying certain closure conditions which are discussed further in Andrews 1972b. Basically, in a general model every wff must have a value with respect to each assignment.
A model is said to be finite iff its domain of individuals is finite. Every finite model for Q0 is standard (Andrews 2002, Theorem 5404), but every set of sentences of Q0 which has infinite models also has nonstandard models (Andrews2002, Theorem 5506).
An understanding of the distinction between standard and nonstandard
models can clarify many phenomena. For example, it can be shown that
there is a model
M
= ⟨{Dα}α,
ℑ⟩
in which
D is infinite, and all the domains
Dα
are countable. Thus
D
is infinite, and all the domains
Dα
are countable. Thus
D and
Dο
and
Dο are both countably infinite, so there must be a bijection h between
them. However, Cantor's Theorem (which is provable in type theory and
therefore valid in all models) says that
D
are both countably infinite, so there must be a bijection h between
them. However, Cantor's Theorem (which is provable in type theory and
therefore valid in all models) says that
D has more subsets than members. This seemingly paradoxical situation
is called Skolem's Paradox. It can be resolved by looking carefully at
Cantor's Theorem, i.e.,
∼∃gο
has more subsets than members. This seemingly paradoxical situation
is called Skolem's Paradox. It can be resolved by looking carefully at
Cantor's Theorem, i.e.,
∼∃gο
 ∀fο
∀fο ∃j
∃j [gο
[gο
 j
j =
fο
=
fο ],
and considering what it means in a model. The theorem says that there is
no function
g ∈
Dο
],
and considering what it means in a model. The theorem says that there is
no function
g ∈
Dο
 from
D
from
D into
Dο
into
Dο which has every set
fο
which has every set
fο ∈
Dο
∈
Dο in its range. The usual interpretation of the statement is that
Dο
in its range. The usual interpretation of the statement is that
Dο is bigger (in cardinality) than
D
is bigger (in cardinality) than
D .
However, what it actually means in this model is that h
cannot be in
Dο
.
However, what it actually means in this model is that h
cannot be in
Dο
 .
Of course, M must be nonstandard.
.
Of course, M must be nonstandard.
While the Axiom of Choice is presumably true in all standard models,
there is a nonstandard model for
Q0
in which
AC is false (Andrews 1972b). Thus,
AC
is false (Andrews 1972b). Thus,
AC is not provable in
Q0.
is not provable in
Q0.
Thus far, investigations of model theory for Church's type theory have been far less extensive than for first-order logic. Nevertheless, there has been some work on methods of constructing nonstandard models of type theory and models in which various forms of extensionality fail, models for theories with arbitrary (possibly incomplete) sets of logical constants, and on developing general methods of establishing completeness of various systems of axioms with respect to various classes of models. Relevant papers include Andrews 1971, 1972a,b, Benzmüller et al. 2004, Brown 2004, Brown 2007, and Muskens 2007.
3. Metatheory
3.1 λ-conversion
The first three rules of inference in Section 1.3.1 are called rules of λ-conversion. If D and E are wffs, we write D conv E to indicate that D can be converted to E by applications of these rules. This is an equivalence relation between wffs. A wff D is in β-normal form iff it has no well-formed parts of the form [[λxαBβ]Aα]. Every wff is convertible to one in β-normal form. Indeed, every sequence of contractions (applications of rule 2, combined as necessary with alphabetic changes of bound variables) of a wff is finite; obviously, if such a sequence cannot be extended, it terminates with a wff in β-normal form. (This is called the strong normalization theorem.) By the Church-Rosser Theorem, this wff in β-normal form is unique modulo alphabetic changes of bound variables. For each wff A we denote by ↓A the first wff (in some enumeration) in β-normal form such that A conv ↓A. Then D conv E if and only if ↓D = ↓E.
By using the Axiom of Extensionality one can obtain the following derived rule of inference:
η-Contraction. Replace a well-formed part [λyβ[Bαβyβ]] of a wff by Bαβ, provided yβ does not occur free in Bαβ.
This rule and its inverse (which is called η-Expansion) are sometimes used as additional rules of λ-conversion. See Church 1941, Stenlund 1972, and Barendregt 1984 for more information about λ-conversion.
3.2 Higher-order Unification
Consider the following:
Definition. A higher-order unifier for a pair ⟨A,B⟩ of wffs is a substitution θ for free occurrences of variables such that θA and θB have the same β-normal form. A higher-order unifier for a set of pairs of wffs is a unifier for each of the pairs in the set.
Higher-order unification differs from first-order unification (Baader & Snyder 2001) in a number of important respects. In particular:
- Even when a unifier for a pair of wffs exists, there may be no most general unifier (Gould 1966).
- Higher-order unification is undecidable (Huet 1973b), even in the "second-order" case (Goldfarb 1981).
Nevertheless, an algorithm has been devised (Huet 1975, Jensen & Pietrzykowski 1976) which will find a unifier for a set of pairs of wffs if one exists. The algorithm generates a search tree, certain branches of which may not terminate. See Dowek 2001 for more information.
3.3 A Unifying Principle
Smullyan's Unifying Principle was introduced in Smullyan 1963 (see also Smullyan 1995) as a tool for deriving a number of basic metatheorems about first-order logic in a uniform way. It was extended to elementary type theory (the system T of section Section 1.3.2) in Andrews 1971 by applying ideas in Takahashi 1967.
This Unifying Principle for T has been used to establish cut-elimination for T in Andrews 1971 and completeness proofs for various systems of type theory in Huet 1973a, Kohlhase 1995, and Miller 1983. We first give a definition and then state the principle.
Definition. A property Γ of finite sets of wffs0 is an abstract consistency property iff for all finite sets S of wffs0, the following properties hold (for all wffs A, B):
- If Γ(S), then there is no atom A such that A ∈ S and [∼A] ∈ S.
- If Γ(S ∪ {A}), then Γ(S ∪ ↓A}).
- If Γ(S ∪ {∼ ∼A}), then Γ(S ∪ {A}).
- If Γ(S ∪ {[A ∨ B]}), then Γ (S ∪ {A}) or Γ(S ∪ {B}).
- If Γ (S ∪ {∼[A ∨ B]}), then Γ(S ∪ {∼A,∼B}).
- If Γ(S ∪ {Πο(οα)Aοα}), then Γ(S ∪ {Πο(οα)Aοα, AοαBα}) for each wff Bα.
- If Γ(S ∪ {∼Πο(οα)Aοα}), then Γ(S ∪ {∼Aοαcα}), for any variable or parameter cα which does not occur free in Aοα or any wff in S.
Note that consistency is an abstract consistency property.
Unifying Principle for T .
If Γ is an abstract consistency property and Γ(S), then S is consistent in T .
Here is a typical application of the Unifying Principle. Suppose there is a procedure M which can be used to refute sets of sentences, and we wish to show it is complete for T . For any set of sentences, let Γ(S) mean that S is not refutable by M, and show that Γ is an abstract consistency property. Now suppose that A is a theorem of T . Then {∼A} is inconsistent in T , so by the Unifying Principle not Γ({∼A}), so {∼A} is refutable by M.
Kohlhase (1993) extended the Unifying Principle to systems with extensionality. This extended principle was used in Benzmüller & Kohlhase 1998a to obtain a completeness proof for a system of extensional higher-order resolution. This extended principle also appears in Kohlhase 1998, where it is used to obtain a completeness proof for an extensional higher-order tableau calculus, which has been implemented under the name HOT (Konrad 1998). In Benzmüller et al. 2004 the principle and associated completeness proofs are presented in a very general way which allows for various possibilities concerning the treatment of extensionality and equality.
3.4 Cut-elimination
Cut-elimination proofs for Church's type theory, which are often closely related to such proofs (Prawitz 1968, Takahashi 1967 and 1970) for other formulations of type theory, may be found in Andrews 1971, Dowek & Werner 2003, and Brown 2004.
3.5 Expansion Proofs
An expansion proof is a generalization of the notion of a Herbrand expansion of a theorem of first-order logic; it provides a very elegant, concise, and nonredundant representation of the relationship between the theorem and a tautology which can be obtained from it by appropriate instantiations of quantifiers and which underlies various proofs of the theorem. Miller (1987) proved that a wff A is a theorem of elementary type theory if and only if A has an expansion proof.
In Brown 2004 and Brown 2007, this concept is generalized to that of an extensional expansion proof to obtain an analogous theorem involving type theory with extensionality.
3.6 The Decision Problem
Since type theory includes first-order logic, it is no surprise that
most systems of type theory are undecidable. However, one may look for
solvable special cases of the decision problem. For example, the
system
Q01
obtained by adding to
Q0
the additional axiom
∀x ∀y
∀y [x
[x =y
=y ]
is decidable.
]
is decidable.
Although the system T of elementary type theory is analogous to first-order logic in certain respects, it is a considerably more complex language, and special cases of the decision problem for provability in T seem rather intractable for the most part. Information about some very special cases of this decision problem may be found in Andrews 1974, and we now summarize this.
A wff of the form ∃x1…∃xn[A=B] is a theorem of T iff there is a substitution θ such that θA conv θB. In particular, ⊦A=B iff A conv B, which solves the decision problem for wffs of the form [A=B]. Naturally, the circumstance that only trivial equality formulas are provable in T changes drastically when axioms of extensionality are added to T . ⊦∃xβ[A=B] iff there is a wff Eβ such that ⊦[λxβ[A=B]]Eβ, but the decision problem for the class of wffs of the form ∃xβ[A=B] is unsolvable.
A wff of the form ∀x1…∀xnC, where C is quantifier-free, is provable in T iff ↓C is tautologous. On the other hand, the decision problem for wffs of the form ∃zC, where C is quantifier-free, is unsolvable. (By contrast, the corresponding decision problem in first-order logic with function symbols is known to be solvable (Maslov 1967).) Since irrelevant or vacuous quantifiers can always be introduced, this shows that the only solvable classes of wffs of T in prenex normal form defined solely by the structure of the prefix are those in which no existential quantifiers occur.
4. Automation
Computer systems for proving theorems of Church's type theory (or extensions of it) interactively or automatically include HOL (Gordon 1988, Gordon & Melham 1993), TPS (Andrews et al. 1996, Andrews & Brown 2006), LEO (Benzmüller 1999, Benzmüller & Kohlhase 1998b), LEO-II (Benzmüller et al. 2008), HOT (Konrad 1998), PVS (Owre et al. 1996), Shankar 2001), and ProofPower. Extensive work using Church's type theory to verify hardware and software is discussed in Gordon 1986 and the TPHOLS conferences. A survey of ideas on automating the development of proofs in Church's type theory may be found in Andrews 2001.
Bibliography
- Andrews, P., 1963, "A Reduction of the Axioms for the Theory of Propositional Types", Fundamenta Mathematicae, 52: 345–350.
- Andrews, P., 1971, "Resolution in Type Theory", Journal of Symbolic Logic, 36: 414–432.
- Andrews, P., 1972a, "General Models and Extensionality", Journal of Symbolic Logic, 37: 395–397.
- Andrews, P., 1972b, "General Models, Descriptions, and Choice in Type Theory", Journal of Symbolic Logic, 37: 385–394.
- Andrews, P., 1974, "Provability in Elementary Type Theory", Zeitschrift fur Mathematische Logic und Grundlagen der Mathematik, 20: 411–418.
- Andrews, P., 2001, "Classical Type Theory", in A. Robinson and A. Voronkov (eds.), Handbook of Automated Reasoning, Volume 2/Chapter 15, Amsterdam: Elsevier Science, pp. 965–1007.
- Andrews, P., 2002, An Introduction to Mathematical Logic and Type Theory: To Truth Through Proof, Dordrecht: Kluwer Academic Publishers, second edition.
- Andrews, P., Bishop, M., Issar, S., Nesmith, D., Pfenning, F., and Xi, H., 1996, "TPS: A Theorem Proving System for Classical Type Theory", Journal of Automated Reasoning, 16: 321–353.
- Andrews, P., and Brown, C., 2006, "TPS: A Hybrid Automatic-Interactive System for Developing Proofs", Journal of Applied Logic, 4: 367-395.
- Baader, F., and Snyder, W., 2001, "Unification theory", in A. Robinson and A. Voronkov (eds.), Handbook of Automated Reasoning, Volume 1/Chapter 8, Amsterdam: Elsevier Science, pp. 445–533.
- Barendregt, H. P., 1984, The λ-Calculus, Series: Studies in Logic and the Foundations of Mathematics, Amsterdam: North-Holland.
- Benzmüller, C., 1999, Equality and Extensionality in Automated Higher-Order Theorem Proving, Ph.D. dissertation, Computer Science Department, Universität des Saarlandes.
- Benzmüller, C., Brown, C., and Kohlhase, M., 2004, "Higher-Order Semantics and Extensionality", Journal of Symbolic Logic, 69: 1027–1088.
- Benzmüller, C., and Kohlhase, M., 1998a, "Extensional Higher-Order Resolution", in Kirchner and Kirchner 1998, pp. 56–71.
- Benzmüller, C., and Kohlhase, M., 1998b, "System Description: LEO — A Higher-Order Theorem Prover", in Kirchner and Kirchner 1998, pp. 139–143.
- Benzmüller, C., Paulson, L, Theiss, F., and Fietzke, A., 2008, "LEO-II - A Cooperative Automatic Theorem Prover for Higher-Order Logic." in A. Armando and P. Baumgartner and G. Dowek (eds.), Fourth International Joint Conference on Automated Reasoning (IJCAR'08), Lecture Notes in Artifical Intelligence, volume 5195, Springer, pp. 162–170.
- Brown, C., 2004, Set Comprehension in Church's Type Theory, Ph.D. dissertation, Department of Mathematical Sciences, Carnegie Mellon University.
- Brown, C., 2007, Automated Reasoning in Higher-Order Logic: Set Comprehension and Extensionality in Church's Type Theory, Studies in Logic: Logic and Cognitive Systems, volume 10, College Publications.
- Büchi, J. R., 1953, "Investigation of the Equivalence of the Axiom of Choice and Zorn's Lemma from the Viewpoint of the Hierarchy of Types", Journal of Symbolic Logic, 18: 125–135.
- Church, A., 1932, "A set of postulates for the foundation of logic (1)", Annals of Mathematics, 33: 346–366.
- Church, A., 1940, "A Formulation of the Simple Theory of Types", Journal of Symbolic Logic, 5: 56–68.
- Church, A., 1941, The Calculi of Lambda-Conversion. Series: Annals of Mathematics Studies, Volume 6, Princeton: Princeton University Press.
- Dowek, G., 2001, "Higher-Order Unification and Matching", in A. Robinson and A. Voronkov, editors, Handbook of Automated Reasoning, Volume 2/Chapter 16, Amsterdam: Elsevier Science, pp. 1009–1062.
- Dowek, G., and Werner, B., 2003, "Theorem Proving Modulo", Journal of Symbolic Logic, 68: 1289–1316.
- Farmer, W., 2008, "Seven Virtues of Simple Type Theory", Journal of Applied Logic, 6:267–286.
- Gödel, K., 1931, "Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I", Monatshefte für Mathematik und Physik, 38: 173–198.
- Goldfarb, W., 1981, "The Undecidability of the Second-Order Unification Problem", Theoretical Computer Science, 13: 225–230.
- Gordon, M., 1986, "Why higher-order logic is a good formalism for specifying and verifying hardware", in G. J. Milne and P. A. Subrahmanyam (eds.), Formal Aspects of VLSI Design, Amsterdam: North-Holland, pp. 153–177.
- Gordon, M. J. C., 1988, "HOL: A Proof Generating System for Higher-Order Logic", in G. Birtwistle and P.A. Subrahmanyam (eds.), VLSI Specification, Verification, and Synthesis, Dordrecht: Kluwer Academic Publishers, pp. 73–128.
- Gordon, M.J., and Melham, T.F., 1993, Introduction to HOL: A Theorem-Proving Environment for Higher-Order Logic, Cambridge: Cambridge University Press.
- Gould, W. E., 1966, A Matching Procedure for ω-order Logic, Ph.D. dissertation, Mathematics Department, Princeton University.
- Henkin, L., 1950, "Completeness in the Theory of Types", Journal of Symbolic Logic, 15: 81–91.
- Henkin, L., 1963, "A Theory of Propositional Types", Fundamenta Mathematicae, 52: 323–344.
- Hilbert, D., 1928, "Die Grundlagen der Mathematik", Abhandlungen aus dem mathematischen Seminar der Hamburgischen Universität, 6: 65–85; translated in van Heijenoort 1967, pp. 464–479.
- Huet, G. P., 1973a, "A Mechanization of Type Theory", in Proceedings of the Third International Joint Conference on Artificial Intelligence (Stanford University), Los Altos, CA: William Kaufman, pp. 139–146.
- Huet, G. P., 1973b, "The Undecidability of Unification in Third-order Logic", Information and Control, 22: 257–267.
- Huet, G. P., 1975, "A Unification Algorithm for Typed λ-Calculus", Theoretical Computer Science, 1: 27–57.
- Jensen, D. C., Pietrzykowski, T., 1976, "Mechanizing ω-Order Type Theory Through Unification", Theoretical Computer Science, 3: 123–171.
- Kirchner, C., and Kirchner, H. (eds.), 1998, Proceedings of the 15th International Conference on Automated Deduction, Series: Lecture Notes in Artificial Intelligence, Volume 1421, London: Springer-Verlag.
- Kohlhase, M., 1993, "A Unifying Principle for Extensional Higher-Order Logic", Technical Report 93-153, Department of Mathematics, Carnegie Mellon University.
- Kohlhase, M., 1995, "Higher-Order Tableaux", in P. Baumgartner, R. Hähnle, and J. Posegga (eds.), Theorem Proving with Analytic Tableaux and Related Methods (4th International Workshop, TABLEAUX '95, Schloß; Rheinfels, St. Goar, Germany, May 1995), Series: Lecture Notes in Artificial Intelligence, Volume 918, Berlin: Springer-Verlag.
- Kohlhase, M., 1998, "Higher-Order Automated Theorem Proving", in Wolfgang Bibel and Peter Schmitt (eds.), Automated Deduction — A Basis for Applications, Volume 1, Dordrecht: Kluwer, pp. 431–462.
- Konrad, K., 1998, "HOT: A Concurrent Automated Theorem Prover Based on Higher-Order Tableaux", in J. Grundy and M. Newey (eds.), Theorem Proving in Higher Order Logics (11th International Conference, TPHOLs'98, Canberra, Australia), Series: Lecture Notes in Computer Science, Volume 1479, Berlin: Springer-Verlag, pp. 245–261.
- Maslov, S. Ju., 1967, "An Inverse Method for Establishing Deducibility of Nonprenex Formulas of Predicate Calculus", Soviet Mathematics Doklady, 8: 16–19.
- Miller, D. A., 1983, Proofs in Higher-Order Logic, Ph.D. dissertation, Mathematics Department, Carnegie Mellon University.
- Miller, D. A., 1987, "A Compact Representation of Proofs", Studia Logica, 46/4: 347–370.
- Muskens, R., 2007, "Intensional Models for the Theory of Types", Journal of Symbolic Logic, 72: 98–118.
- Owre, S., Rajan, S., Rushby, J.M., Shankar, N., and Srivas, M., 1996, "PVS: Combining Specification, Proof Checking, and Model Checking", in R. Alur and T. A. Henzinger (eds.), Computer-Aided Verification, Series: Lecture Notes in Computer Science, Volume 1102, Berlin: Springer-Verlag, pp. 411–414.
- Prawitz, D., 1968, "Hauptsatz for Higher Order Logic", Journal of Symbolic Logic, 33: 452–457.
- Quine, W. V., 1937, "Logic Based on Inclusion and Abstraction", Journal of Symbolic Logic, 2: 145–152.
- Russell, B., 1903, The Principles of Mathematics, Cambridge: Cambridge University Press.
- Russell, B., 1908, "Mathematical Logic as Based on the Theory of Types", American Journal of Mathematics, 30: 222–262; reprinted in van Heijenoort 1967, pp. 150–182.
- Schönfinkel, M., 1924, "Über die Bausteine der mathematischen Logik", Mathematische Annalen, 92: 305–316; translated in van Heijenoort 1967, pp. 355–366.
- Shankar, N., 2001, "Using Decision Procedures with a Higher-Order Logic", in R. J. Boulton and P. B. Jackson (eds.), Theorem Proving in Higher Order Logics (14th international conference, TPHOLs 2001, Edinburgh, Scotland), Series: Lecture Notes in Computer Science, Volume 2152, Berlin: Springer-Verlag, pp. 5–26.
- Smullyan, R. M., 1963, "A Unifying Principle in Quantification Theory", Proceedings of the National Academy of Sciences (U.S.A.), 49: 828–832.
- Smullyan, R. M., 1995, First-Order Logic, New York: Dover, second corrected edition.
- Stenlund, S., 1972, λ-terms and Proof Theory, Dordrecht: D. Reidel.
- Takahashi, M., 1967, "A Proof of Cut-Elimination Theorem in Simple Type Theory", Journal of the Mathematical Society of Japan, 19: 399–410.
- Takahashi, M., 1970, "A System of Simple Type Theory of Gentzen Style with Inference on Extensionality, and the Cut Elimination in it", Commentarii Mathematici Universitatis Sancti Pauli, 18: 129–147.
- Tarski, A., 1923, "Sur le terme primitif de la Logistique", Fundamenta Mathematicae, 4: 196–200; translated in Tarski 1956, 1–23.
- Tarski, A., 1956, Logic, Semantics, Metamathematics, Oxford: Oxford University Press.
- van Heijenoort, J., 1967, From Frege to Gödel. A Source Book in Mathematical Logic 1879–1931, Cambridge, MA: Harvard University Press.
- Whitehead, A. N., and Russell, B., 1927a, Principia Mathematica, Volume 1, Cambridge: Cambridge University Press, second edition.
- Whitehead, A. N., and Russell, B., 1927b, "Incomplete Symbols", in Whitehead & Russell 1927a, 66–84; reprinted in van Heijenoort 1967, 216–223.
- Yasuhara, M., 1975, "The Axiom of Choice in Church's Type Theory" (abstract), Notices of the American Mathematical Society, 22 (January): A-34.
Other Internet Resources
- Mathematics Genealogy Project, Mathematics Department, North Dakota State University.
Related Entries
artificial intelligence: logic and | logic: classical | reasoning: automated | Russell, Bertrand | type theory
Acknowledgments
Portions of this material are adapted from Andrews 2002 and Andrews 2001, with permission from the author and Elsevier.

