Stanford Encyclopedia of Philosophy
Supplement to Nineteenth Century Geometry
A Modern Formulation of Riemann’s Theory
The multidimensional continua that Riemann was concerned with are
essentially instances of what is now known as a real
n-dimensional smooth manifold. For brevity, call them
‘n-manifolds’. (For example, a sphere, a
Möbius strip and the surface of a Henry Moore sculpture may be
regarded as 2-manifolds; the spacetimes models of current cosmology
are 4-manifolds.) Conditions (a) -- (c) provide a full
characterization of n-manifolds.
(a) An n-manifold M
is a set of points that can be pieced together from partially
overlapping patches, such that every point of
M
lies in at least one patch.
(b) M is endowed with a neighborhood structure
(a topology) such that, if U is a patch of
M, there is a continuous one-one mapping
f of U onto some region of
Rn, with continuous inverse
f-1.
(Rn denotes here the collection of all real
number n-tuples, with the standard topology generated by the open
balls.)
f is a coordinate system or
chart of
M; the k-th number in the
n-tuple assigned by a chart
f to a point P in
f’s patch is called the k-th
coordinate of P by
f; the k-th coordinate
function of chart
f is the real-valued function that
assigns to each point of the patch its k-th coordinate by
f.
(c) There is a collection A of charts of
M,
which contains at least one chart defined on each patch of
M
and is such that, if g and h belong to
A, the composite mappings
h  g-1 and
g
g-1 and
g  h-1
--- known as coordinate transformations --- are
differentiable to every order wherever they are well defined. (Denote
the real number n-tuple
<a1, ... , an>
by a. The mapping
h
h-1
--- known as coordinate transformations --- are
differentiable to every order wherever they are well defined. (Denote
the real number n-tuple
<a1, ... , an>
by a. The mapping
h  g-1
is well defined at a if a is the valued assigned by g
to some point P of
M
to which h also assigns a value. Suppose that the latter value h(P)
= <b1, ... ,bn> = b;
then, b =
h
g-1
is well defined at a if a is the valued assigned by g
to some point P of
M
to which h also assigns a value. Suppose that the latter value h(P)
= <b1, ... ,bn> = b;
then, b =
h  g-1(a).
Since h
g-1(a).
Since h  g-1
maps a region of Rn into Rn, it
makes sense to say that
h
g-1
maps a region of Rn into Rn, it
makes sense to say that
h  g-1
is differentiable.) Such a collection A is
called an
atlas.[*]
g-1
is differentiable.) Such a collection A is
called an
atlas.[*]
It is the pair
<M, A>
that, strictly speaking, is an n-manifold, in the sense defined
above. If
<M1,A1>
and
<M2,A2>
are an n-manifold and an m-manifold, respectively, it
makes good sense to say that a mapping
f of M1 into
M2 is differentiable at a point P of
M1 if, for a chart h defined at P and a chart g
defined at
f(P), the composite mapping
g  f
f  h-1
is differentiable at h(P). (Condition (c) implies that the
fulfillment of this requirement does not depend on the choice of h
and g.)
f is differentiable if it is
differentiable at every point of M1.
h-1
is differentiable at h(P). (Condition (c) implies that the
fulfillment of this requirement does not depend on the choice of h
and g.)
f is differentiable if it is
differentiable at every point of M1.
Let
<M,A>
be an n-manifold. To each point P of
M
one associates a vector space, which is known as the tangent
space at P and is denoted by
TPM.
The idea is based on the intuitive notion of a plane tangent to a
surface at a given point. It can be constructed as follows. Let
 be a one-one differentiable mapping of a real open interval I
into
M.
We can think of the successive values of
be a one-one differentiable mapping of a real open interval I
into
M.
We can think of the successive values of
 as
forming the path of a point that moves through
M
during a time interval represented by I. We call
as
forming the path of a point that moves through
M
during a time interval represented by I. We call
 a curve in M
(parametrized by u
a curve in M
(parametrized by u  I). Put
I). Put
 (t0) = P
for a fixed number t0 in
I. Consider the collection F(P) of all differentiable
real-valued functions defined on some neighborhood of P. With the
ordinary operations of function addition and multiplication by a
constant, F(P) has the structure of a vector space. Each
function
f in F(P) varies smoothly
with u, along the path of
(t0) = P
for a fixed number t0 in
I. Consider the collection F(P) of all differentiable
real-valued functions defined on some neighborhood of P. With the
ordinary operations of function addition and multiplication by a
constant, F(P) has the structure of a vector space. Each
function
f in F(P) varies smoothly
with u, along the path of
 ,
in some neighborhood of P. Its rate of variation at P =
,
in some neighborhood of P. Its rate of variation at P =
 (t0)
is properly expressed by the derivative
d(f
(t0)
is properly expressed by the derivative
d(f
 )/du at
u = t0. As
f ranges over F(P), the
value of
d(f
)/du at
u = t0. As
f ranges over F(P), the
value of
d(f
 )/du
at u =
t0 is apt to vary in R. So we
have here a mapping of F(P) into R, which we denote by
)/du
at u =
t0 is apt to vary in R. So we
have here a mapping of F(P) into R, which we denote by
 (u). It is in fact a
linear function and therefore a vector in the dual space F*(P)
of real-valued linear functions on F(P). Call it the
tangent to
(u). It is in fact a
linear function and therefore a vector in the dual space F*(P)
of real-valued linear functions on F(P). Call it the
tangent to
 at P. The tangents at P to all the curves whose paths go through P
span an n-dimensional subspace of F*(P). This subspace is, by
definition, the tangent space
TPM.
The tangent spaces at all points of an n-manifold
M
can be bundled together in a natural way into a 2n-manifold
TM.
The projection mapping
at P. The tangents at P to all the curves whose paths go through P
span an n-dimensional subspace of F*(P). This subspace is, by
definition, the tangent space
TPM.
The tangent spaces at all points of an n-manifold
M
can be bundled together in a natural way into a 2n-manifold
TM.
The projection mapping
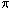 of
TM onto
M assigns to
each tangent vector v in
TPM
the point
of
TM onto
M assigns to
each tangent vector v in
TPM
the point 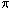 (v)
at which v is tangent to
M. The structure
<TM,M,
(v)
at which v is tangent to
M. The structure
<TM,M,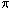 >
is the tangent bundle over
M.
A vector field on M is a section of
TM, i.e., a differentiable mapping
f of
M into
TM such that
>
is the tangent bundle over
M.
A vector field on M is a section of
TM, i.e., a differentiable mapping
f of
M into
TM such that
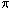
 f
sends each point P of
M to itself;
such a mapping obviously assigns to P a vector in
TPM.
f
sends each point P of
M to itself;
such a mapping obviously assigns to P a vector in
TPM.
Any vector space V is automatically associated with other
vector spaces, such as the dual space V* of linear functions
on V, and the diverse spaces of multilinear functions on
V, on V*, and on any possible combination of V
and V*. This holds, of course, for each tangent space of an
n-manifold
M. The dual of
TPM
is known as the cotangent space at P. There is a natural way of
bundling together the cotangent spaces of M
into a 2n-manifold, the cotangent bundle. Generally speaking, all the
vector spaces of a definite type associated with the tangent and
cotangent spaces of
M
can be naturally bundled together into a k-manifolds (for suitable
integers k, depending on the nature of the bundled items). A section
of any of these bundles is a tensor field on
M
(of rank r, if the bundled objects are r-linear functions).
A Riemannian metric g on the n-manifold
<M,A>
is a tensor field of rank 2 on
M.
Thus, g assigns to each P in
M a bilinear function
gP on
TPM. For any P in
M and any vectors v, w, in
TPM,
gP must meet these requirements:
(i) gP(v,w) =
gP(w,v)
(symmetry)
(ii) gP(v,w) =
0 for all vectors
w in
TPM if and only if
v is the 0-vector (non-degeneracy)
(iii) gP(v,v) > 0 unless
v is the 0-vector (positive definiteness).
It is worth noting that the so-called Lorentzian metrics defined by
relativity theory on its spacetime models meet requirements (i) and
(ii), but not (iii), and are therefore usually said to be
semi-Riemannian.
The length
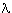 (v) of a vector v in
TPM is defined by
|
(v) of a vector v in
TPM is defined by
|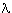 (v)|2 =
gP(v,v). Let
(v)|2 =
gP(v,v). Let
 be a curve in
M. Let
be a curve in
M. Let
 (u) be the tangent to
(u) be the tangent to
 at
the point
at
the point  (u). The length of
(u). The length of
 ’s path from
’s path from
 (a) to
(a) to
 (b) is measured by the integral
(b) is measured by the integral

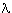 (
( (u))du
(u))du
Thus, in Riemannian geometry, the length of the tangent vector
 (u) bears witness to
the advance of curve g as it passes through the point
(u) bears witness to
the advance of curve g as it passes through the point
 (u). The definition of the
length of a curve leads at once to the notion of a geodesic (or
straightest) curve, which is characterized by the fact that its
length is extremal; in other words, a geodesic is either the greatest
or the shortest among all the curves that trace out neighboring paths
between the same two points.
(u). The definition of the
length of a curve leads at once to the notion of a geodesic (or
straightest) curve, which is characterized by the fact that its
length is extremal; in other words, a geodesic is either the greatest
or the shortest among all the curves that trace out neighboring paths
between the same two points.
In his study of curved surfaces, Gauss introduced a real-valued
function, the Gaussian curvature, which measures a surface’s
local deviation from flatness in terms of the surface’s intrinsic
geometry. Riemann extended this concept of curvature to Riemannian
n-manifolds. He observed that each geodesic through a point in such a
manifold is fully determined by its tangent vector at that
point. Consider a point P in a Riemannian n-manifold
<M,A,g>
and two linearly independent vectors v and w in
TPM. The geodesics
determined by all linear combinations of v and w form a
2-manifold about P, with a definite Gaussian curvature
KP(v,w) at P. The real number
KP(v,w) measures the curvature of
M at P in the ‘surface direction’ (Riemann 1854,
p. 145) fixed by v and w. Riemann (1861) thought up a
global mapping, depending on the metric g, that yields the
said values
KP(v,w) on appropriate
arguments P, v and w. Nowadays this object is conceived
as a tensor field of rank 4, which assigns to each point P in a
Riemannian n-manifold
<M,A,g>
a 4-linear function on the tangent space
TPM.
It is therefore known as the Riemann tensor. Given the above
definition of
KP(v,w) it is clear
that, if n = 2, the Riemann tensor reduces to the Gaussian
curvature function.
Copyright © 1999 by
Roberto Torretti
Universidad de Chile
cordua@rdc.cl
Return to Nineteenth Century Geometry
First published: July 26, 1999
Content last modified: July 26, 1999
 g-1 and
g
g-1 and
g  h-1
--- known as coordinate transformations --- are
differentiable to every order wherever they are well defined. (Denote
the real number n-tuple
<a1, ... , an>
by a. The mapping
h
h-1
--- known as coordinate transformations --- are
differentiable to every order wherever they are well defined. (Denote
the real number n-tuple
<a1, ... , an>
by a. The mapping
h  g-1
is well defined at a if a is the valued assigned by g
to some point P of
M
to which h also assigns a value. Suppose that the latter value h(P)
= <b1, ... ,bn> = b;
then, b =
h
g-1
is well defined at a if a is the valued assigned by g
to some point P of
M
to which h also assigns a value. Suppose that the latter value h(P)
= <b1, ... ,bn> = b;
then, b =
h  g-1(a).
Since h
g-1(a).
Since h  g-1
maps a region of Rn into Rn, it
makes sense to say that
h
g-1
maps a region of Rn into Rn, it
makes sense to say that
h  g-1
is differentiable.) Such a collection A is
called an
atlas.[*]
g-1
is differentiable.) Such a collection A is
called an
atlas.[*]
 be a one-one differentiable mapping of a real open interval I
into
M.
We can think of the successive values of
be a one-one differentiable mapping of a real open interval I
into
M.
We can think of the successive values of
 I). Put
I). Put
 (u). It is in fact a
linear function and therefore a vector in the dual space F*(P)
of real-valued linear functions on F(P). Call it the
tangent to
(u). It is in fact a
linear function and therefore a vector in the dual space F*(P)
of real-valued linear functions on F(P). Call it the
tangent to
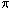 of
TM onto
M assigns to
each tangent vector v in
TPM
the point
of
TM onto
M assigns to
each tangent vector v in
TPM
the point 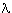 (v) of a vector v in
TPM is defined by
|
(v) of a vector v in
TPM is defined by
|