Compositionality
Anything that deserves to be called a language must contain meaningful expressions built up from other meaningful expressions. How are their complexity and meaning related? The traditional view is that the relationship is fairly tight: the meaning of a complex expression is fully determined by its structure and the meanings of its constituents—once we fix what the parts mean and how they are put together we have no more leeway regarding the meaning of the whole. This is the principle of compositionality, a fundamental presupposition of most contemporary work in semantics.
Proponents of compositionality typically emphasize the productivity and systematicity of our linguistic understanding. We can understand a large—perhaps infinitely large—collection of complex expressions the first time we encounter them, and if we understand some complex expressions we tend to understand others that can be obtained by recombining their constituents. Compositionality is supposed to feature in the best explanation of these phenomena. Opponents of compositionality typically point to cases when meanings of larger expressions seem to depend on the intentions of the speaker, on the linguistic environment, or on the setting in which the utterance takes place without their parts displaying a similar dependence. They try to respond to the arguments from productivity and systematicity by insisting that the phenomena are limited, and by suggesting alternative explanations.
- 1. Clarifications
- 2. Formal statement
- 3. Arguments for compositionality
- 4. Arguments against compositionality
- Bibliography
- Other internet resources
- Related entries
1. Clarifications
There are many theses called ‘the principle of compositionality’. The following can serve as a common reference point:
(C) The meaning of a complex expression is determined by its structure and the meanings of its constituents.
Important variants of the compositionality principle will be presented below in a form most similar to (C) to facilitate comparisons.[1] When formulating more precise versions it is crucial to keep the pre-theoretical intuitions that led many to accept compositionality firmly in mind.
1.1 Languages
The principle of compositionality is normally taken to quantify over expressions of some particular language L:
(C′) For every complex expression e in L, the meaning of e in L is determined by the structure of e in L and the meanings of the constituents of e in L.
Questions of structure and constituency are settled by the syntax of L, while the meanings of simple expressions are given by the lexical semantics of L. Compositionality entails (although on many elaborations is not entailed by) the claim that syntax plus lexical semantics determines the entire semantics for L.
It makes a big difference whether L is a natural or an artificial language. Syntactic and semantic questions about a natural language are settled by and large through empirical investigation; syntactic and semantic questions about an artificial language are settled usually by checking what the appropriate stipulations are. Prima facie, natural languages might turn out not to be compositional, whereas many artificial languages were designed to meet such a requirement. (Compositionality is a bonus when it comes to proof-checking in computer languages, or inductive proofs in logical calculi.) Unless explicitly noted, talk of compositionality is to be taken as talk of compositionality of some particular natural language, or of natural languages in general.
If thought is a kind of language, we can raise the question whether it is compositional. Thought would not have to be much like Swahili or the language of set theory for the question to make sense, but we do need the assumptions that thoughts have meanings (and so, presumably, are not themselves meanings) and that they have meaningful constituents. These assumptions follow from the language of thought hypothesis. Those who reject this hypothesis may still speak of the compositionality of thought—but only in an extended sense.
What would such an extended sense be? The key to generalizing compositionality for non-linguistic representational systems is to relax the syntactic ideas of constituency and structure. Consider, for example, the No-Left-Turn sign:
This could be viewed as a complex sign decomposable into meaningful features—the shape, the color pattern, the arrow, etc. These features are the analogues of simple expressions: they appear in many other complex signs and they appear to contribute more or less uniformly to their meanings.
Once we have an initial grip on what counts as a constituent and how constituents compose we can legitimately raise the question whether this system of representations is compositional.[2] We may even be able to answer it.[3]
There is a major debate within the philosophy of mind between proponents of classical cognitive architecture and proponents of connectionism. The debate is typically presented as a debate about compositionality, but it is not exactly about that. The issue tends to be whether there are such things as meaningful constituents of thought (perhaps in the extended sense in which traffic signs can be said to have meaningful constituents), and if there are, whether these contribute the same thing (presumably their meaning) to all thoughts in which they occur. If the answer to the first question is negative, the question of compositionality does not arise. If the answer to the first question is positive, the second is independent of compositionality. (It could be that thought-constituents contribute always the same thing to a thought of which they are constituents, but these contributions, even together with the way the constituents are combined, severely underdetermine the meaning of the thought. And it could be that thought-constituents contribute different things to different thoughts—depending on the intentions of the thinker, or perhaps the surroundings of the thinking—but these variable contributions, plus the way the constituents are combined, fully determine the meaning of the thought.) The debate about connectionism is more closely related to the question whether reverse compositionality holds (cf. section 1.5.4.)
1.2 Meaning
The principle of compositionality is not committed to a specific conception of meaning. In fact, it is frequently announced as a principle that is applicable to whatever a semantic theory might assign to expressions of a language. Furthermore, although the reference of an arbitrary expression is definitely not something one would normally call its ‘meaning’, versions of the following principle are frequently called ‘the principle of compositionality’:
(Cref) For every complex expression e in L, the reference of e in L is determined by the structure of e in L and the references of the constituents of e in L.
(I use the word ‘reference’ here roughly the way Frege used his ‘Bedeutung’ after 1892. But it could be taken the way Barwise and Perry use ‘reference’, the way Lewis uses ‘extension’, or the way Kaplan uses ‘content’. The differences are significant, but they do not matter for present purposes.) To avoid confusion, we should call this the principle of compositionality of reference, and (C) the principle of compositionality of meaning; when I speak of compositionality unqualified, what is meant is always the latter. Since the arguments in favor of compositionality tend to be based on general considerations about linguistic understanding—which, I shall suppose amounts to nothing more or less than understanding what linguistic expressions mean[4] —proponents of (Cref) have a choice to make. They can advocate (Cref) on different grounds or they can claim that an appropriate theory of the sort that assigns (relative to a variety of factors) references to expressions can serve as a theory of meaning.
We should not be dogmatic about what we are willing to call ‘meaning’, but we should not abandon all constraints either. We should, for example, not allow that expressions serve as their own meaning, unless we are willing to abandon all pre-teoretic notions of meaning and make compositionality a vacuous requirement. It is trivial that we can compositionally assign something to each expression of a language, but it does not follow that it is trivial to adequately assign meanings to them.
Similar considerations apply to more subtle attempts to trivialize compositionality. Consider a famous result due to Zadrozny (1994). Given a set S of strings generated from an arbitrary alphabet via concatenation and a meaning function m which assigns the members of an arbitrary set M to the members of S, we can construct a new meaning function μ such that for all s, t ∈ S μ(s.t) = μ(s)(μ(t)) and μ(s)(s) = m(s). What this shows is that we can turn an arbitrary meaning function into a compositional one,[5] as long as we replace the old meanings with new ones from which they are uniformly recoverable.[6] But this does not show that it is a trivial matter to devise an adequate meaning assignment for S. Since synonymy according to μ does not coincide with synonymy according to m, we should not accept the claim that μ is as adequate as m; and since someone ignorant of m could assign entities to members of S following μ, we should not accept the claim that the values of the latter as much deserve to be called meanings as the values of the former. (For further discussion of Zadrozny's result, see Kazmi and Pelletier (1998), Westerståhl (1998), Dever (1999).)
Compositionality obviously constrains what meanings might be. But the constraints apply only to the meanings of complex expressions—for all (C) tells us the meanings of simple expressions could be tables and chairs. For let the meanings of complex expressions be interpreted logical forms, i.e., phrase structure trees with the meanings of the constituent lexical items assigned to their terminal nodes. In a fairly straightforward sense the meanings of lexical items are then parts of the meanings of complex expressions in which they occur, and so the meanings of complexes are determined from the relevant tables and chairs together with their syntactic mode of composition; for similar remarks see Horwich (1997).
That compositionality does not constrain lexical meaning might appear paradoxical at first, but the source of paradox is just instability in how the label ‘compositionality’ is used. Sometimes compositionality is said to be that feature in a language (or non-linguistic representational system) which best explains the productivity and systematicity of our understanding; cf. Fodor (2001): 6. (C) is but one of the features such explanations use—others include the context-invariance of most lexical meaning, the finiteness of the lexicon, the relative simplicity of syntax, and probably much else. These features together put significant constraints on what lexical meanings might be; cf. the papers collected in Fodor and Lepore (2002) and Szabó (2004).
1.3 Structure
Much of what was said above about the need to constrain what counts as meaning applies to structure as well. Janssen (1986) has a proof that we can turn any meaning assignment on a recursively enumerable set of expressions into a compositional one, as long as we can replace the syntactic operations with different ones. If we insist—as we should—that any acceptable semantic theory must respect what syntax tells us about the structure of complex expressions, this result says nothing about the possibility of providing an adequate compositional semantics; cf. Westerståhl (1998).[7] The moral of the result is that although commitment to compositionality requires allegiance to no particular sect of syntacticians, one cannot be oblivious to syntactic evidence in semantic theorizing.
(C) does not require the kind of tight correspondence between syntax and semantics we intuitively associate with compositionality. To illustrate this, consider a view, according to which the meaning of a declarative sentence s is the set of possible worlds where s is true. According to such a view, tautologies are synonymous, even though (since Rudolf presumably has some tautological beliefs and lacks others) sentences resulting from embedding tautologies under ‘Rudolf believes that…’ are not. (I also assume a strightforward semantics for propositional attitudes without hidden indexicals or tacit quantification.) Intuitively, this is a violation of compositionality. Still, the semantics is not in conflict with (C): tautologies might differ structurally or in the meaning of their constituents, which could explain how their embedding can yield non-synonymous sentences; cf. Carnap (1947) and Lewis (1970).
To rule a semantic theory like this one non-compositional, we need to demand that the meaning of a complex expression be determined by its immediate structure, and the meanings of its immediate constituents. (The immediate structure of an expression is the syntactic mode its immediate constituents are combined. e is an immediate constituent of e′ iff e is a constituent of e′ and e′ has no constituent of which e is a constituent.)
(Clocal) For every complex expression e in L, the meaning of e in L is determined by the immediate structure of e in L and the meanings of the immediate constituents of e in L.
Call the strengthened principle local compositionality, and (C) global compositionality; when unqualified, ‘compositionality’ should be taken as global. The local principle is more intuitive, and semanticists frequently presuppose it. In fact, some theorists assume not only (Clocal), but also that concatenation is uniformly interpreted as functional application, or perhaps as conjunction; cf. Pietroski (2005). If so, we can omit explicit talk of structre and say simply that the meanings of complex expressions are determined by the meanings of their immediate constituents. But clearly, appeal to our ability to understand novel expressions in itself provides no direct support for such a strong claim.
1.4 Determination
If a language is compositional, it cannot contain a pair of non-synonymous complex expressions with identical structure and pairwise synonymous constituents. (This follows from the fact that the same structure and the same meanings of constituents cannot determine more than one meaning within a language.) Surprisingly, as the principle of compositionality is usually construed, it remains silent on the possibility of such pair of complex expressions existing in distinct languages. But this is an open violation of what we normally mean by determination. (This follows from the fact that the qualification ‘within a language’ in the above parenthetical remark does no work whatsoever.)
Here is an illustration from Szabó (2000b). Suppose English is compositional. Take two of its non-synonymous sentences—say, ‘Elephants are grey’ and ‘Julius Caesar was murdered on the ides of March’—and define Crypto-English as the language with the same expressions, the same syntax and almost the same semantics as English. The only difference is that if a sentence is synonymous in English with one of the two designated sentences, then it is synonymous with the other in Crypto-English. We assumed English is compositional and hence that there is no pair of non-synonymous complex expressions in English with identical structure and pairwise synonymous constituents. Trivially, the same must hold for Crypto-English as well. But intuitively, Crypto-English is not compositional. The structure and the meanings of constituents of the Crypto-English sentence ‘Elephants are grey’ cannot determine what this sentence means in Crypto-English—if they did then the structure and the meanings of constituents of the English sentence ‘Elephants are grey’ would have to determine what ‘Julius Caesar was murdered on the ides of March’ means in English.
If we want a better match with our intuitions, we must demand more from a compositional language than the mere existence of a function from structures and the meanings of parts to the meanings of wholes. One possibility would be to put constraints on this function—we could demand, for example that it be computable, or perhaps even that the computation be reasonably quick. But the above example shows that such a strengthening would not solve the problem: if computing the meanings of complex expressions is easy in English, it will not be hard in Crypto-English either. We might instead opt for the following strengthening of (C):
(Ccross) For every complex expression e in L, the meaning of e in L is functionally determined through a single function for all possible human languages by the structure of e in L and the meanings of the constituents of e in L.
Call the strengthened principle cross-linguistic compositionality, and (C)—when ‘determine’ is simply read as ‘functionally determine’ and we may have different functions for different languages—language-bound compositionality. Note that formal languages that ara designed to sataisfy language-bound compositionality may nonetheless violate cross-lingutic compositionality simply because their syntax or the meanings of their constituetns violate some universal constraint on human languages. Note also that whatever the epistemic status of other version of the principle of compositionality might be, cross-lingutic compositionality is clearly an empirical hypothesis.[8]
When speaking of compositionality unqualified, I will always mean language-bound compositionality. Again, the stronger principle is much closer to our pre-theoretic intuitions and it is often tacitly assumed in practice. But the traditional considerations in favor of compositionality support the weaker thesis only.
1.5 Related principles
We have now eight different interpretations for the seemingly simple claim that a certain language is compositional. The claim might concern reference or meaning, it might be local or global, and it might be construed in a cross-linguistic or a language-bound manner. There are also a number of related principles worth mentioning that are often discussed along with (and are occasionally confused with) compositionality.
1.5.1 Substitutivity
Consider first the often cited principle that says that substitution of synonyms is always meaning preserving. As stated, the principle requires clarification. For one thing, not every case of replacement counts as substitution: the expression we replace with its synonym within a larger expression must be a constituent of the larger expression. (Otherwise, as Geach pointed out, the synonymy of ‘Plato was bald’ with ‘Baldness was an attribute of Plato’ would guarantee the synonymy of ‘The philosopher whose most eminent pupil was Plato was bald’ and ‘The philosopher whose most eminent pupil was baldness was an attribute of Plato’; cf. Geach (1965):110.)
In addition, we need to separate two issues: whether substitution of synonymns can turn a meaningful expression into a meaningless one, and whether it can turn a meaningful expression into an expression with a different meaning. The principle that rules out the former possibility was first proposed by Husserl (1913):318, and it is usually stated in terms of the notion of a semantic category. Two expressions belong to the same semantic category just in case they are intersubstitutable within any meaningful expression salva significatione (without loss of meaningfulness). According to Husserl's principle:
(H) Synonyms belong in the same semantic category.
(H) is a rather controversial — intuitively, there are many synonyms that are not everywhere intersubstitutable. For example, ‘likely’ and ‘probable’ mean pretty much the same even though ‘Jacques is likely to leave’ is meaningful while ‘Jacques is probable to leave’ is arguably not; cf. Gazdar (1985): 32.[9] And — more controversially — there might be synonyms that are almost nowhere intersubstitutable: ‘quick’ and ‘quickly’ are good candiadates.
The principle that rules out the possibility that substitution of synonyms could turn a meaningful expression into one with a different meaning comes in two versions:
(Ssingular) If two meaningful expressions differ only in that one is the result of substituting a synonym for a constituent within the other then the two expressions are synonyms.
(Splural) If two meaningful expressions differ only in that one is the result of substituting some synonyms for some constituents within the other then the two expressions are synonyms.
Assuming the language under discussion has a grammar that requires that each constituent of a meaningful complex expression be itself meaningful (Splural) is equivalent to language-bound, local compositionality of meaning. Assuming in addition that the language satisfies (H), (Ssingular) is equivalent to (Splural); cf. Hodges (2001) Theorem 4.
1.5.2 The rule-to-rule principle
Sometimes the claim that L is compositional is presented directly as a claim about the relationship between its syntax and semantics. The following thesis is often called the rule-to-rule principle:
(RR) To every syntactic rule corresponds a semantic rule that assigns meanings to the output of the syntactic rule on the basis of the meanings of its inputs.
How strong a claim (RR) is depends on what counts as a rule. If an arbitrary function deserves that name, the rule-to-rule principle is equivalent to language-bound local compositionality of meaning. But if we insist—quite plausibly—that a semantic rule must be computable (or perhaps easily computable) the rule-to-rule principle is stronger than that. And if we assume that rules must have some sort of psychological reality, (RR) says something completely different from (C).
1.5.3 The primacy of words
Ordinarily when we say that something determines something else we think of the former as being causally or explanatorily prior to the latter. Although the principle of compositionality is usually not understood in this way, sometimes philosophers read it as a principle that asserts the priority of word meaning over sentence meaning, or more generally, the priority of the meanings of lexical items over the meanings of complex expressions:
(P) Complex expressions have their meanings in virtue of their structure and the meanings of their constituents.
(P) is often thought to be in tension with the idea that each expression has the meaning it does in virtue of the way it is used within some linguistic community. The conflict is supposed to arise because (i) the use of an expression is exhausted by its employment in speech acts, and (ii) it is sentences, not words, that can be employed to make speech acts. Against this, it can be argued that referring is among the speech acts speakers routinely perform and that this speech act is done with words, not sentences. One might try to replace (i) with a stronger claim, for example, that the use of an expression is exhausted by its employment in asserting, asking, commanding, and a few of other speech acts not including referring. But even if true the stronger claim may not save the argument against (P) because, at least prima facie, we can make assertions with isolated words as well; cf. Stainton (2006). Davis (2003) develops a detailed theory of meaning that combines (P) with a version of the use theory of mening.
To say that there is no easy argument against (P) is a far cry from saying that it must be true. It is important to keep in mind that (P) is significantly stronger than (C) and that the usual arguments in favor of compositionality cannot by themselves justify it.
1.5.4 Frege's context principle
In section 60 of the Foundations of Arithmetic Frege famously declares that only within a complete sentence do words have meaning. This has come to be referred to in the literature as Frege's context principle. Frege writes that “it is enought if the sentence as whole has meaning; therby also its parts obtain their meanings”.[10] On the face of it, this asserts that words have their meanings in virtue of the meaning of sentences in which they occur as constituents. This is incompatible with (P), but not with (C). Even if words are meaningful only because they occur as constituents within sentences, there could still be a function (perhaps even a single function across all possible human languages) that maps the structure of a sentence and the meanings of its constituent words to the meaning of that sentence.
There is an alternative way to construe Frege's principle, a way that makes it a determination claim, not a primacy claim. To state it in a form that matches the generality of (C) we should drop the talk of words and sentences, and talk instead about complex expressions and their constituents:
(Fall) The meaning of an expression is determined by the meanings of all complex expressions in which it occurs as a constituent.
Like the principle of compositionality, Frege's context principle can be intepreted as a claim about reference or meaning, locally or globally, in a language-bound manner or cross-lingutically. Compositionality is about bottom-up meaning-determination, while the context principle about top-down meaning-determination. As long as it is not understood as a causal or explanatory relation determination can be symmetric, so any version of (C) is compatible with the corresponding version of (Fall).
There is a strenghtening of (Fall), according to which the meaning of an expression is determined not only by the meanings of all expressions in which it occurs as a constituent, but by the meaning of any one of these expressions:
(Fany) The meaning of an expression is determined by the meaning of any complex expression in which it occurs as a constituent.
(Fany) is an immediate consequence of the converse of (C)— sometimes called reverse compositionality — according to which the meaning of a complex expression determines the structure of the expression and the meanings of its constituents. (Fodor (1998b), Fodor and Lepore (2001), Pagin (2003) adocate reverse compositionality; Patterson (2005), Robbins (2005), Johnson (2006) are among its opponents. The debate is complex, in part because at least some proponents of reverse compositionality advocate it only for the languge of thought; cf. Fodor (2001).)
(Fany) is a very strong thesis and most standard semantic theories are incompatible with it. Take, for example, a simple Carnapian semantics that assigns to each sentence the set of possible worlds where it is true. Suppose we are considering a language that contains the standard logical operators, and so any sentence is a constituent of a necessarily true sentence. Since the meaning of a necessary truth is the set of all possible worlds, this set would have to determine the meanings of all sentences in the language, which is absurd.
A principle of intemediate strength between (Fall) and (Fany) is (Fcof):
(Fcofinal) The meaning of an expression is determined by the meanings of all expressions within any cofinal set of expressions.
(A cofinal set of expressions is a set such that any expression occurs as a constituent in at least one member of the set. Except for very odd languages, the set of all expressions within the language in which some given expression occurs as a constituent is one of many cofinal sets of expressions, so (Fall) follows from (Fcofinal) but not the other way around. That (Fcofinal) follows from (Fany) but not the other way around is trivial.)
The interest of (Fcofinal) comes from the fact that it appears to be in conflict with a Quine's thesis of the indeterminacy of translation (taken as a thesis that implies the indeterminacy of meaning). Assume that the set of all observation sentences is cofinal within a reasonably large fragment of a natural language and that the meaning of an observation sentence is identical to its stimulus meaning — (Fcofinal) ensures then that the meanings of all the words are determined within our fragment. Recently there has been an attempt to show that (Fcofinal) follows from less controversial claims, and perhaps even from claims that Quine himself was committed to; cf. Werning (2004). The heart of Werning's argument is Theorem 14 from Hodges (2001), which states that a meaning assignment to a cofinal set of expressions that satisfies (H) has a unique extension to a meaning assignment to all expressions that satisfies (H), (Ssingular) and its converse. (Note that (Ssingular) and its converse amount to a strong thesis about the individuation of meanings: two meaningful expressions are synonyms if and only if substituting one for the other in a third meaningful expression never results in an expression with a different meaning.) Of course, this has a bite against Quine's thesis only if (H), (Ssingular) and its converse are plausibly true — which is dubious; cf. Leitgeb (2005).
1.5.5 The building principle
The claim that L is compositional is often taken to mean that the meaning of an arbitrary complex expression in L is built up from the meanings of its constituents in L—call this the building principle for L. This is a fairly strong claim, at least if we take the building metaphor seriously. For then the meanings of complex expressions must themselves be complex entities whose structure mirrors that of the sentence; cf. Frege (1892), Frege (1919). This presumably entails but is not entailed by cross-linguistic local compositionality of meaning.
2. Formal statement
Montague (1970) suggested a perspicuous way to capture the principle of compositionality formally. The key idea is that compositionality requires the existence of a homomorphism between the expressions of a language and the meanings of those expressions.
Let us think of the expressions of a language as a set upon which a
number of operations (syntactic rules) are defined. Let us require
that syntactic rules always apply to a fixed number of expressions and
yield a single expression, and let us allow that syntactic rules be
undefined for certain expressions. So, a syntactic algebra is
a partial algebra E
=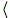 E,
(Fγ)γ∈Γ
E,
(Fγ)γ∈Γ ,
where E is the set of (simple and complex) expressions and
every Fγ is a partial syntactic operation on
E with a fixed arity. The syntactic algebra is interpreted
through a meaning-assignment m, a function from E to
M, the set of available meanings for the expressions of
E.
,
where E is the set of (simple and complex) expressions and
every Fγ is a partial syntactic operation on
E with a fixed arity. The syntactic algebra is interpreted
through a meaning-assignment m, a function from E to
M, the set of available meanings for the expressions of
E.
Consider now F, a k-ary syntactic operation on E. m is F-compositional just in case there is a k-ary partial function G on M such that whenever F(e1,…,ek) is defined,
m(F(e1,…,ek)) = G(m(e1),…,m(ek)).
(In English: there is a partial function from the meanings of e1,…,ek to the meaning of the expression built from e1,…,ek through an application of the syntactic rule F.)
Finally, we can say that m is compositional
simpliciter just in case m is
F-compositional for each syntactic operation in
E. Whenever m is compositional, it induces
the semantic algebra M
=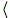 M,
(Gγ)γ∈Γ
M,
(Gγ)γ∈Γ on M, and it is a homomorphism between E
and M; cf. Westerståhl (1998). (For details,
variants, and formal results, see Jannssen (1986), (1997) and Hodges
(2001).)
on M, and it is a homomorphism between E
and M; cf. Westerståhl (1998). (For details,
variants, and formal results, see Jannssen (1986), (1997) and Hodges
(2001).)
Since there are no restrictions on what m assigns to members of E, the formal statement captures both compositionality of reference and compositionality of meaning. As stated, the principle captures local language-bound compositionality: it requires that each application of each syntactic rule within a language be matched by an application of an appropriate semantic function. To capture cross-linguistic compositionality is easy: all we need to say is that the expressions within E are the expressions of all possible human languages. (Of course, if we allow the syntactic algebra to contain expressions of different languages, we may want to insist that syntactic operations map expressions of a language onto complex expressions of the same language and that they remain undefined for cases when their argument positions are filled by expressions from different languages.[11]) To capture global compositionality is more complicated.
Here is an attempt. Let us say that the expressions e and e′ are local equivalents just in case they are the results of applying the same syntactic operation to lists of expressions such that corresponding members of the lists are synonymous. (More formally: for some natural number k there is a k-ary F in E, and there are some expressions e1,…,ek, e1′,…,ek′ in E, such that e = F(e1,…,ek), e′ = F(e1′,…,ek′), and for every 1≤ i ≤ k, m(ei) = m(ei′).) It is clear that m is locally compositional just in case locally equivalent pairs of expressions are all synonyms. Let us say that the expressions e and e′ are global equivalents just in case they are the results of applying the same syntactic operation to lists of expressions such that corresponding members of the lists are either (i) simple and synonymous or (ii) complex and globally equivalent. (Here is the recursive definition more formally. Let us say that the expressions e and e′ are 1-global equivalents just in case they are synonymous simple expressions. Let us say that the expressions e and e′ are n-global equivalents just in case for some natural number k there is a k-ary F in E, and there are some expressions e1,…,ek, e1′,…,ek′ in E, such that e = F(e1,…,ek), e′ = F(e1′,…,ek′), and for every 1 ≤ i ≤ k there is a 1 ≤ j < n such that ei and ei′ are j-global equivalents. Finally, let us say that the expressions e and e′ are global equivalents just in case for some natural number n they are n-global equivalents.)[12] I suggest that m is globally compositional just in case globally equivalent pairs of expressions are all synonyms.
3. Arguments for compositionality
The simplest argument for compositionality is that it is supported by intuitions many claim to have about meaning and structure. Although there are interesting putative counterexamples (see section 4.2.) they probably can be explained away through modest revisions of our syntactic and/or semantic theories. This defense is reasonable but much too modest. For even if it succeeds in convincing some who aren't already convinced, it leaves us all in the dark why compositionality is true. Defenders of compositionality should do better than this.
3.1 Productivity
The argument most often used to support compositionality is based on productivity. It goes back (at least) to Frege, who claimed that “the possibility of our understanding sentences which we have never heard before rests evidently on this, that we can construct the sense of a sentence out of parts that correspond to words.” (Frege 1914?: 79) The argument is an inference to the best explanation, which can be expanded and rephrased without assuming that meanings are Fregean senses.[13]
Argument from productivity: Since competent speakers can understand a complex expression e they never encountered before, it must be that they (perhaps tacitly) know something on the basis of which they can figure out, without any additional information, what e means. If this is so, something they already know must determine what e means. And this knowledge cannot plausibly be anything but knowledge of the structure of e and knowledge of the meanings of the simple constituents of e.
To bolster the claim that we do, in fact, understand complex expressions we never heard before, philosophers often appeal to unboundedness: although we are finite beings we have the capacity to understand each of an infinitely large set of complex expressions. Although there are dissenters—e.g., Ziff (1974)—the claim that natural languages contain infinitely many complex expressions is plausible.[14] But it is equally plausible that nobody who reads this entry the first time has ever encountered this very sentence before, and consequently, the detour through cardinality considerations seems superfluous. Occasionally, the fact that natural languages are learnable is also used to argue for compositionality. This is not an independent argument: the reason it is remarkable that we can learn a natural language is that once we have learnt it our understanding is productive. If we could not understand expressions we never encountered before, without detailed empirical study we could not rule out the hypothesis that we learned the language in question by rote.
The first thing to point out about the argument from productivity is that it is an argument in favor of (C)—global language-bound compositionality of meaning. As it stands, it provides no reason for believing anything this principle does not entail; in particular it cannot establish (Cref), (Clocal), or (Ccross).
As an argument for global language-bound compositionality, it can be criticized on the ground that considerations of this sort simply cannot establish a universal claim. Suppose someone suggests that the complex expression e is a counterexample to (C). The fact that we tend to understand all sorts of complex expressions we never heard before does not mean that we would understand e on the first encounter. But suppose we would. Still, even if in general we tend to understand complex expressions we never heard before in virtue of our knowledge of their structure and the meanings of their simple constituents, we might understand e in some other way. General considerations of productivity cannot rule out isolated exceptions to compositionality. (Isolated putative exceptions are often declared to be idioms—expressions whose syntactic complexity is only apparent. But unless we are given clear non-semantic grounds for singling out idioms, the move is question-begging. Such criteria have been proposed, but they tend to be rather controversial; cf. Nunberg, Sag and Wasow (1994).)
If we lower our sights and seek to prove nothing more than the claim that natural languages by and large obey global language-bound compositionality of meaning, the argument from productivity is a strong one.
3.2 Systematicity
Another argument in favor of compositionality is based on systematicity, the fact that there are definite and predictable patterns among the sentences we understand. For example, anyone who understands ‘The rug is under the chair’ can understand ‘The chair is under the rug’ and vice versa. This is also an inference to the best explanation, and can be summarized as follows:
Argument from systematicity: Anyone who understands a complex expression e and e′ built up through the syntactic operation F from constituents e1,…,en and e1′,…,en′ respectively, can also understand any other meaningful complex expression e″ built up through F from expressions among e1,…,en, e1′,…,en′. So, it must be that anyone who knows what e and e′mean is in the position to figure out, without any additional information, what e″ means. If this is so, the meaning of e and e′ must jointly determine the meaning of e″. But the only plausible way this could be true is if the meaning of e determines F and the meanings of e1,…,en, the meaning of e′ determines F and the meanings of e1′,…,en′, and F and the meanings of e1,…,en , e1′,…,en′ determine the meaning of e″.
Although the arguments from productivity and systematicity are usually alluded to in the same breath, they are very different considerations. Unlike the main premise of the former, the main premise of the latter is anything but obvious. Particular instances are plausible enough: it seems reasonable that anyone who can understand ‘The dog is asleep’ and ‘The cat is awake’ can also understand ‘The dog is awake’ and ‘The cat is asleep’, and that anyone who can understand ‘black dog’ and ‘white cat’ can also understand ‘black cat’ and ‘white dog’. But do all who understand ‘within an hour’ and ‘without a watch’ also understand ‘within a watch’ and ‘without an hour’? And do all who understand ‘halfway closed’ and ‘firmly believed’ also understand ‘halfway believed’ and ‘firmly closed’? As Johnson (2004) argues, the claim that natural languages are systematic presupposes a natural non-overlapping linguistic categorization of all the expressions. The existence of such a categorization is a bold empirical hypothesis.
Fodor (1998b) does offer an empirical argument in favor of systematicity. The idea is that if complex expressions could be understood without understanding their constituents then it is unclear how exposure to a corpus made up almost entirely of complex expressions could suffice to learn the meanings of lexical items. But, as a matter of empirical fact, children learn the meanings of words by encountering them almost exclusively within other expressions. However, as Robbins (2005) points out, this observation can at best lead one to concluse that understanding a suitably large set of complex expressions in which a given expression occurs as a constituent suffices for understanding the constituent itself. It does not show that understanding any complex expression suffices for understanding its constituents.
The arguments from productivity and systematicity differ in what they aim to prove. First, the argument from systematicity proves something weaker than (any version of) compositionality. If we run the argument for the pair of sentences ‘The dog is asleep’ and ‘The cat is awake’ we can conclude that the meanings of ‘the dog’, ‘the cat’, ‘is asleep’ and ‘is awake’ plus predication determine the meaning of ‘The dog is awake’. It does not follow that the meanings of ‘the dog’ and ‘is awake’ plus predication do that. Second, if this problem can be fixed somehow, the argument from systematicity proves not only global, but local compositionality: it tells us that the meanings of immediate constituents and immediate structure fix the meanings of complex expressions. Finally, if successful, the argument from systematicity proves not only a version of the compositionality principle, but also reverse compositionality. We are invited to conclude that the meaning of an arbitrary complex expression determines its immediate structure and the meanings of its immediate constituents; cf. section 1.5.4, Fodor and Lepore (2001): 59, Pagin (2003): 292.
As with the argument from productivity, the argument from systematicity is unable to screen out isolated counterexamples. Still, it is a strong consideration in favor of the claim that natural languages by and large obey language-bound local compositionality of meaning and its reverse.
4. Arguments against compositionality
Considerations regarding productivity and systematicity are powerful. It does seem to many that the explanation of these phenomena that presupposes compositionality is not only the best, but also the only one imaginable. So, before I survey some of the putative counterexamples to compositionality from the semantic literature, to bolster the imagination I will discuss a simple non-linguistic case where our understanding is productive and systematic despite apparent lack of compositionality in the system of representations.
4.1 How compositionality might fail
Consider the Algebraic notation for chess.[15] Here are the basics. The rows of the chessboard are represented by the numerals 1, 2, … , 8; the columns are represented by the lower case letters a, b, … , h. The squares are identified by column and row; for example b5 is at the intersection of the second column and the fifth row. Upper case letters represent the pieces: K stands for king, Q for queen, R for rook, B for bishop, and N for knight. Moves are typically represented by a triplet consisting of an upper case letter standing for the piece that makes the move and a sign standing for the square where the piece moves. There are five exceptions to this: (i) moves made by pawns lack the upper case letter from the beginning, (ii) when more than one piece of the same type could reach the same square, the sign for the square of departure is placed immediately in front of the sign for the square of arrival, (iii) when a move results in a capture an x is placed immediately in front of the sign for the square of arrival, (iv) the symbol 0-0 represents castling on the king's side, (v) the symbol 0-0-0 represents castling on the queen's side. + stands for check, and ++ for mate. The rest of the notation serves to make commentaries about the moves and is inessential for understanding it.
Someone who understands the Algebraic notation must be able to follow descriptions of particular chess games in it and someone who can do that must be able to tell which move is represented by particular lines within such a description. Nonetheless, it is clear that when someone sees the line Bb5 in the middle of such a description, knowing what B, b, and 5 mean will not be enough to figure out what this move is supposed to be. It must be a move to b5 made by a bishop, but we don't know which bishop (not even whether it is white or black) and we don't know which square it is coming from. All this can be determined by following the description of the game from the beginning, assuming that one knows what the initial configurations of figures are on the chessboard, that white moves first, and that afterwards black and white move one after the other. But staring at Bb5 itself will not help.
The first moral of the example is that we can have productive and systematic understanding of representations even if we do not understand complex representations merely by understanding their simple components and the way those components are combined. The reason this could happen is that all who understand the system know certain things (e.g., the initial configuration of pieces and the order of moves) from which they can figure out the missing information (e.g., which figure is moving and from where).
The second moral is that—given certain assumptions about meaning in chess notation—we can have productive and systematic understanding of representations even if the system itself is not compositional. The assumptions in question are that (i) the description I gave in the first paragraph of this section fully determines what the simple expressions of chess notation mean and also how they can be combined to form complex expressions, and that (ii) the meaning of a line within a chess notation determines a move. One can reject (i) and argue, for example, that the meaning of B in Bb5 contains an indexical component and within the context of a description, it picks out a particular bishop moving from a particular square. One can also reject (ii) and argue, for example, that the meaning of Bb5 is nothing more than the meaning of ‘some bishop moves from somewhere to square b5’—utterances of Bb5 might carry extra information but that is of no concern for the semantics of the notation. Both moves would save compositionality at a price. The first complicates considerably what we have to say about lexical meanings; the second widens the gap between meanings of expressions and meanings of their utterances. Whether saving compositionality is worth either of these costs (or whether there is some other story to be told about our understanding of the Algebraic notation) is by no means clear. For all we know, Algebraic notation might be non-compositional.
4.2 How compositionality allegedly fails
I will discuss briefly four famous putative counterexamples to the compositionality of English from the semantic literature. In each case, I will also indicate what reasonable responses to the challenges might look like.
Putative counterexamples to (C) are always complex expressions whose meaning appears to depend not only on the meanings of their constituents and on their structure but on some third factor as well. Sometimes this third factor is linguistic context: what a complex expression means seems to depend in part on how it is embedded into a sentence (cf. 4.2.1) or a sequence of sentences (cf. 4.2.2). In other cases the third factor is extra-linguistic: the setting in which the complex expression is used (cf. 4.2.3) or someone's beliefs about what the expression means (cf. 4.2.4).
Such putative counterexamples are not all on the same level. Although they all violate the letter of (C), some could be more easily reconciled with productivity and systematicity than others. If it turned out that in order to interpret an embedded sentence, one needs information about the embedding sentence as well we would have to conclude that the algorithm for calculating the meanings of complex expressions is more complicated then we thoguht. But a complicated algorithm is still an algorithm and the core explanation of how we understand complex expressions would remain untouched. By contrast, if it turned out that in order to interpret a sentence we must know all sorts of ephemeral non-linguistic facts we would have to conclude that the fact that we can reliably understand all sorts of unfamiliar sentences is a mystery. Those who accept putative counterexamples of this latter kind must provide alternative explanations for productivity and systematicity.
4.2.1 Conditionals
Consider the following minimal pair:
(1) Everyone will succeed if he works hard.
(2) No one will succeed if he goofs off.
A good translation of (1) into a first-order language is (1′). But the analogous translation of (2) would yield (2′), which is inadequate. A good translation for (2) would be (2″) but it is unclear why. We might convert ‘¬∃’ to the equivalent ‘∀¬’ but then we must also inexplicably push the negation into the consequent of the embedded conditional.
(1′) ∀x(x works hard → x will succeed)
(2′) ¬∃x (x goofs off → x will succeed)
(2″) ∀x (x goofs off → ¬(x will succeed))
This gives rise to a problem for the compositionality of English, since is seems rather plausible that the syntactic structure of (1) and (2) is the same and that ‘if’ contributes some sort of conditional connective—not necessarily a material conditional!—to the meaning of (1). But it seems that it cannot contribute just that to the meaning of (2). More precisely, the interpretation of an embedded conditional clause appears to be sensitive to the nature of the quantifier in the embedding sentence—a violation of compositionality.[16]
One response might be to claim that ‘if’ does not contribute a conditional connective to the meaning of either (1) or (2)—rather, it marks a restriction on the domain of the quantifier, as the paraphrases under (1″) and (2″) suggest:[17]
(1″) Everyone who works hard will succeed.
(2″) No one who goofs off will succeed.
But this simple proposal (however it may be implemented) runs into trouble when it comes to quantifiers like ‘most’. Unlike (3′), (3) says that those students (in the contextually given domain) who succeed if they work hard are most of the students (in the contextually relevant domain):
(3) Most students will succeed if they work hard.
(3′) Most students who work hard will succeed.
The debate whether a good semantic analysis of if-clauses under quantifiers can obey compositionality is lively and open.[18]
4.2.2 Cross-sentential anaphora
Consider the following minimal pair from Barbara Partee:
(4) I dropped ten marbles and found all but one of them. It is probably under the sofa.
(5) I dropped ten marbles and found nine of them. It is probably under the sofa.
There is a clear difference between (4) and (5)—the first one is unproblematic, the second markedly odd. This difference is plausibly a matter of meaning, and so (4) and (5) cannot be synonyms. Nonetheless, the first sentences are at least truth-conditionally equivalent. If we adopt a conception of meaning where truth-conditional equivalence is sufficient for synonymy, we have an apparent counterexample to compositionality.
Few would insist that the first sentences of (4) and (5) are really synonymous. What is interesting about this example is that even if we conclude that we should opt for a more fine grained conception of meaning, it is not immediately clear how that will account for the contrast between these sentences. The difference is obviously due to the fact that ‘one’ occurs in the first sentence of (4), which is available as a proper antecedent for ‘it’ and that there is nothing in the first sentence of (5) that could play a similar role. Some authors have suggested that the right way to approach this problem is to opt for a dynamic conception of meaning, one that can encode anaphoric possibilities for subsequent sentences.[19]
Interesting though these cases might be, it is not at all clear that we are faced with a genuine challenge to compositionality, even if we want to stick with the idea that meanings are just truth-conditions. For it is not clear that (5) lacks the normal reading of (4)—on reflection it seems better to say that the reading is available even though it is considerably harder to get. (Contrast this with an example due to—I think—Irene Heim: ‘They got married. She is beautiful.’ This is like (5) because the first sentence lacks an explicit antecedent for the pronoun in the second. Nonetheless, it is clear that the bride is said to be beautiful.) If the difference between (4) and (5) is only this, it is no longer clear that we must accept the idea that they must differ in meaning.
4.2.3 Adjectives
Suppose a Japanese maple leaf, turned brown, has been painted green. Consider someone pointing at this leaf uttering (6):
(6) This leaf is green.
The utterance could be true on one occasion (say, when the speaker is sorting leaves for decoration) and false on another (say, when the speaker is trying to identify the species of tree the leaf belongs to). The meanings of the words are the same on both occasions and so is their syntactic composition. But the meaning of (6) on these two occasions—what (6) says when uttered in these occasions—is different. As Charles Travis, the inventor of this example puts it: “…words may have all the stipulated features while saying something true, but also while saying something false.”[[20]
At least three responses offer themselves. One is to deny the relevant intuition. Perhaps the leaf really is green if it is painted green and (6) is uttered truly in both situations. Nonetheless, we might be sometimes reluctant to make such a true utterance for fear of being misleading. We might be taken to falsely suggest that the leaf is green under the paint or that it is not painted at all.[21] The second option is to point out that the fact that a sentence can say one thing on one occasion and something else on another is not in conflict with its meaning remaining the same. Do we have then a challenge to compositionality of reference, or perhaps to compositionality of content? Not clear, for the reference or content of ‘green’ may also change between the two situations. This could happen, for example, if the lexical representation of this word contains an indexical element.[22] If this seems ad hoc, we can say instead that although (6) can be used to make both true and false assertions, the truth-value of the sentence itself is determined compositionally.[23]
4.2.4 Propositional attitudes
Perhaps the most widely known objection to compositionality comes from the observation that even if e and e′ are synonyms, the truth-values of sentences where they occur embedded within the clausal complement of a mental attitude verb may well differ. So, despite the fact that ‘eye-doctor’ and ‘ophthalmologist’ are synonyms (7) may be true and (8) false if Carla is ignorant of this fact:
(7) Carla believes that eye doctors are rich.
(8) Carla believes that ophthalmologists are rich.
So, we have a case of apparent violation of compositionality; cf. Pelletier (1994).
There is a sizable literature on the semantics of propositional attitude reports. Some think that considerations like this show that there are no genuine synonyms in natural languages. If so, compositionality (at least the language-bound version) is of course vacuously true. Some deny the intuition that (7) and (8) may differ in truth-conditions and seek explanations for the contrary appearance in terms of implicature.[24] Some give up the letter of compositionality but still provide recursive semantic clauses.[25] And some preserve compositionality by postulating a hidden indexical associated with ‘believe’.[26]
Bibliography
- Barker, S. (1997) ‘Material implication and general indicative conditionals.’ The Philosophical Quarterly 47: 195–211.
- Berg J. (2002) ‘Is semantics still possible?’ Journal of Pragmatics 34: 349–359.
- Cappelen, H. and E. Lepore (2004) ‘Radical and moderate pragmatics: does meaning determine truth-conditions?’ In Z. G. Szabó ed., Semantics vs. Pragmatics. Oxford: Oxford University Press.
- Carnap, R. (1947) Meaning and Necessity. Chicago: University of Chicago Press.
- Chierchia, G. (1995) The Dynamics of Meaning: Anaphora, Presupposition, and the Theory of Grammar. Chicago: University of Chicago Press.
- Cresswell, M. (1986) Structured Meanings. Cambridge, MA: MIT Press.
- Davidson, D. (1965) ‘Theories of meaning and learnable languages.’ Reprinted in D. Davidson, Inquiries into Truth and Interpretation. Oxford: Clarendon Press, 2001: 3–16.
- -----. (1970) ‘Semantics for natural languages.’ Reprinted in D. Davidson, Inquiries into Truth and Interpretation. Oxford: Clarendon Press, 2001: 55–64.
- Davies, M. (1981) Meaning, Quantification, Necessity. London: Routledge.
- Davis, W. (2003) Meaning, Expression, and Thought. Cambridge: Cambridge University Press.
- Dever, J. (1999) ‘Compositionality as methodology.’ Linguistics and Philosophy 22: 311–326.
- Dummett, M. (1973) Frege: Philosophy of Language. Cambridge, MA: Harvard University Press.
- Evans, G. (1982) The Varieties of Reference. Oxford: Clarendon Press.
- von Fintel, K. (1998) ‘Quantifiers and if-clauses.’ The Philosophical Quarterly 48: 209–214.
- Fischer, E. (2000) Linguistic Creativity: Exercises in ‘Philosophical Therapy’. Dordercht: Kluwer.
- Fodor, J. (1991) ‘Why meaning (probably) isnspecial-character:rsquo]t conceptual role.’ Mind and Language 6: 329–343.
- -----. (1996) ‘The pet fish and the red herring: why concepts aren't prototypes’ Cognition 58: 243–276.
- -----. (1998a) ‘There are no recognitional concepts — not even RED.’ In In Critical Condition. Cambrdige, MA: MIT Press, pp. 35–47.
- -----. (1998b) ‘There are no recognitional concepts — not even RED, Part 2: The plot thickens.’ In In Critical Condition. Cambrdige, MA: MIT Press, pp. 49–62.
- -----. (2001a) ‘Language, thought and compositionality.’ Mind and Language 16: 1–15.
- -----. (2001b) ‘Why compositionality won't go away: Reflections on Horwich's “Deflationary” Theory.’ Ratio 14: 350–368.
- Fodor, J. and E. Lepore (1992) Holism: A Shopper's Guide. Oxford: Blackwell.
- -----. (2002) The Compositionality Papers. Oxford: Oxford University Press.
- Fodor, J., and Pylyshyn, Z. (1988). ‘Connectionism and cognitive architecture: A critique.’ Cognition 28: 3–71.
- Frege, G. (1884) The Foundations of Arithmetic. Evanston, IL: Northwestern University Press, 1980.
- -----. (1891) ‘On the law of inertia.’ Reprinted in B. McGuiness, ed., Collected Papers on Mathematics, Logic, and Philosophy. Oxford: Blackwell, 1984: 123–138.
- -----. (1892) ‘On concept and object.’ Reprinted in B. McGuiness, ed., Collected Papers on Mathematics, Logic, and Philosophy. Oxford: Blackwell, 1984: 182–194.
- -----. (1906a) ‘Foundations of geometry/II.’ Reprinted in B. McGuiness, ed., Collected Papers on Mathematics, Logic, and Philosophy. Oxford: Blackwell, 1984: 293–340.
- -----. (1906b) ‘Introduction to logic.’ In Hermes et al. eds., Posthumous Writings. Chicago: Chicago University Press, 1979: 185–196.
- -----. (1914) ‘Logic in mathematics.’ In Hermes et al. eds., Posthumous Writings. Chicago: Chicago University Press, 1979: 201–250.
- -----. (1914?) ‘Letter to Jourdain.’ In G. Gabriel et al. eds., Philosophical and Mathematical Correspondence. Chicago: Chicago University Press, 1980: 78–80.
- -----. (1923) ‘Compound thoughts.’ Reprinted in B. McGuiness, ed., Collected Papers on Mathematics, Logic, and Philosophy. Oxford: Blackwell, 1984: 390–406.
- Gazdar, G., Klein E., Pullum G., and Sag I. (1985) Generalized Phrase Structure Grammar. Cambridge, MA: Harvard University Press.
- Grandy, R. (1990) ‘Understanding and compositionality.’ In J. A. Tomberlin ed., Philosophical Perspectives, 4: Action Theory and Philosophy of Mind. Atascadero, CA: Ridgeview Publishing Co.: 557 – 572.
- Groenendijk J. and M. Stokhoff (1990) ‘Dynamic Montague Grammar.’ In L. Kálmán et al. Proceedings of the 2nd Symposium on Logic and Language. Budapest: Akadémiai Kiadó, 3–48.
- -----. (1991) ‘Dynamic Predicate Logic.’ Linguistics and Philosophy, 14: 39–100.
- Heim , I. (1982) The Semantics of Definite and Indefinite Noun Phrases. PhD. Dissertation, University of Massachusetts at Amherst. Garland Publishing Inc., 1988.
- Hendrix, H. (2001) ‘Compositionality and model-theoretic interpretation.’ Journal of Logic, Language, and Information 10: 29–48.
- Higginbotham, J. (1985) ‘On semantics.’ Linguistic Inquiry 16: 547–593.
- -----. (1986) ‘Linguistic theory and Davidson's program in semantics.’ In E. Lepore ed., Truth and Interpretation: Perspectives on the Philosophy of Donald Davidson. Oxford: Blackwell: 29–48.
- -----. (2003) ‘Conditionals and compositionality.’ In J. Hawthorne ed., Philosophical Perspectives 17: 181–194.
- Hintikka, J. (1981) ‘Theories of truth and learnable languages.’ In S. Kanger and S. Öhman eds., Philosophy and Grammar. Dordrecht: Reidel: 37–58.
- Hintikka, J. and G. Sandu (1997) ‘Game-theoretical semantics.’ In J. van Benthem and A. ter Meulen eds., Handbook of Logic and Language. Amsterdam: Elsevier. 361–410.
- Hodges, W. (1998) ‘Compositionality is not the problem.’ Logic and Logical Philosophy 6: 7–33.
- -----. (2001) ‘Formal features of compositionality.’ Journal of Logic, Language, and Information 10: 7–28.
- Horwich, P. (1997) ‘The composition of meanings.’ Philosophical Review 106: 503–533.
- Husserl, E. (1913) Logische Untersuchungen II/1. Tübingen: Max Niemeyer.
- Janssen, T. M. V. (1983) Foundations and Applications of Montague Grammar. Amsterdam: Mathematisch Centrum.
- -----. (1997) ‘Compositionality.’ In J. van Benthem and A. ter Meulen eds., Handbook of Logic and Language. Amsterdam: Elsevier. 417–473.
- -----. (2001) ‘Frege, contextuality and compositionality.’ Journal of Logic, Language, and Information 10: 115–136.
- Geach, P. (1965) ‘Logical procedures and the identity of expressions.’ Reprinted in Logic Matters Berkeley, CA: University of California Press, 1980, pp. 108–115.
- Johnson, K. (2004) ‘On the systematicity of language and thought.’ Journal of Philosophy 101: 111–139.
- Johnson, K. (2006) ‘On the nature of reverse compositionality.’ Erkenntnis 64: 37–60.
- Kamp, H. (1981) ‘A theory of truth and semantic representation.’ In J. Groenendijk and M. Stokhoff eds., Formal Methods in the Study of Natural Language. Amsterdam: Amsterdam Centre: 277–322.
- Kamp, H. and B. Partee (1995) ‘Prototype theory and compositionality.’ Cognition 57: 129–191.
- Kazmi, A. and F. J. Pelletier (1998) ‘Is compositionality formally vacuous?’ Linguistics and Philosophy 21: 629–633.
- Kratzer, A. (1986) ‘Conditionals.’ Chicago Linguistic Society 22: 1–15.
- Lahav, R. (1989) ‘Against compositionality: the case of adjectives.’ Philosophical Studies 57: 261–279.
- Larson, R. and G. Segal (1995) Knowledge of Meaning: An Introduction to Semantic Theory. Cambridge, MA: MIT Press.
- Leitgeb, H. (2005) ‘Hodges' theorem does not account for determinacy of translation: A reply to Werning.’ Erkenntnis, 62: 411–425.
- Lewis, D. (1970) ‘General semantics.’ Reprinted in Philosophical Papers. Vol. 1. Oxford: Oxford University Press: 189–229.
- -----. (1975) ‘Adverbs of quantification.’ Reprinted in Papers in Philosophical Logic. Cambridge: Cambridge University Press: 5–20.
- -----. (1980) ‘Index, context, and content.’ Reprinted in Papers in Philosophical Logic. Cambridge: Cambridge University Press: 21–44.
- Martin R. L. (1994) The Meaning of Language. Cambridge, MA: MIT Press.
- Montague, R. (1970) ‘Universal Grammar.’ Reprinted in R. Thomason ed., Formal Philosophy. New Haven : Yale University Press, 1974: 222–246.
- Nunberg G., I. A. Sag and T. Wasow (1994) ‘Idioms.’ Language, 70: 491–538.
- Pagin, P. (2003) ‘Communication and strong compositionality.’ Journal of Philosophical Logic 32: 287–322.
- Partee, B. (1984) ‘Compositionality.’ In F. Landman and F. Veltman eds., Varieties of Formal Semantics. Dordrecht: Foris: 281–312.
- -----. (1995) ‘Lexical semantics and compositionality.’ D. Osherson ed., An Invitation to Cognitive Science. Vol. 1. Cambridge, MA: MIT Press: 311–360.
- Patterson, D. (2005) ‘Learnability and compositionality.’ Mind and Language, 20: 326–352.
- Pelletier, F. J. (1994) ‘The principle of semantic compositionality.’ Topoi, 13: 11–24.
- -----. (2001) ‘Did Frege believe in Frege's Principle?’ Journal of Logic, Language, and Information 10: 87–114.
- -----. (2003) ‘Context-dependence and compositionality.’ Mind and Language 18: 148–161.
- Pietroski, P. (2005) Events and semantic architecture. Oxford: Oxford University Press.
- Platts, M. (1979) Ways of Meaning. London: Routledge.
- Robbins, P. (2001) ‘What compositionality still can do.’ Philosophical Quarterly, 51: 328–336.
- Robbins, P. (2005) ‘The myth of reverse compositionality’ Philosophical Studies, 125: 251–275.
- Sainsbury, M. (2001) ‘Two ways to smoke a cigarette’ Ratio 14: 386–406.
- Salmon, N. (1986) Frege's Puzzle. Cambridge, MA: MIT Press.
- Schiffer, S. (1987) The Remnants of Meaning. Cambridge, MA: MIT Press.
- -----. (1991) ‘Does Mentalese have a compositional semantics?’ In B. Loewer and G. Rey eds., Meaning in Mind: Fodor and his Critics. Oxford: Blackwell.
- Stainton, R. (2003) Words and Thoughts. Oxford: Oxford University Press.
- Stanley, J. and Z. G. Szabó (2000) ‘On quantifier domain restriction.’ Mind and Language 15: 219–261.
- Szabó, Z. G. (2000a) Problems of Compositionality. New York: Garland.
- -----. (2000b) ‘Compositionality as supervenience.’ Linguistics and Philosophy 23: 475–505.
- -----. (2000c) ‘Adjectives in context.’ In I. Kenesei and R., Harnish eds., Perspectives on Semantics, Pragmatics, and Discourse. Amsterdam: John Benjamins, pp. 119–146.
- -----. (2004) ‘Review of J. Fodor and E. Lopre The Compositionality Papers.’ Mind 113: 340–344.
- Werning, M. (2004) ‘Compositionality, context, categories and the indeterminacy of translation.’ Erkenntnis, 60: 145–178.
- Werning, M. (2005) ‘Right and wrong reasons for compositionality.’ M. Werning ed., The compositionality of meaning and content. Volume 1: Foundational Issues. Frankfurt: Ontos Verlag: 285–309.
- Westerståhl, D. (1998) ‘On mathematical proofs of the vacuity of compositionality.’ Linguistics and Philosophy 21: 635–643.
- Zadrozny, W. (1994) ‘From compositional to systematic semantics.’ Linguistics and Philosophy 17: 329–342.
- Zeevat, H. (1989) ‘A compositional approach to Discourse Representation Theory.’ Linguistics and Philosophy, 12: 95–131.
Other Internet Resources
- von Fintel, K. and S. Iatridou, (ms.), ‘If and when if-clause can restrict quantifiers.’ [Manuscript available online].
Related Entries
ambiguity | anaphora | conditionals | connectionism | Frege, Gottlob | language of thought hypothesis | logical form | meaning, theories of | pragmatics | propositional attitude reports | reference
Acknowledgments
I thank Tamar Szabó Gendler, Michael Glanzberg, Tamás Mihálydeák, and Jason Stanley for their comments. I am especially grateful to Daniel Rothschild for catching an error and for suggesting the repair in the preliminary draft of section 2. The entry relies at many places on Szabó (2000a). Traffic sign images are from the Manual of Traffic Signs, by Richard C. Moeur.